確率と情報の科学:データ解析のための統計モデリング入門:久保拓弥、岩波書店
第11章 空間構造のある階層ベイズモデル
???????????
場所差の空間相関(spatial correlation)を考慮する統計モデリング。
http://hosho.ees.hokudai.ac.jp/~kubo/ce/CarNormalExample.html
11.1 例題:一次空間上の個体数分布
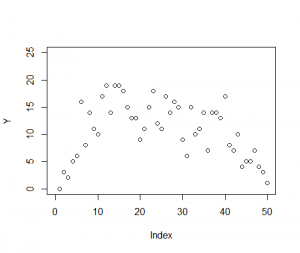
調査区画を50個設定し、それが一本の直線上に等間隔で配置されるとする。
調整区画の番号jは、左から1,2,….,50とする。
ここでは架空のデータ{yi}は場所jごとに平均の異なるポアソン乱数として発生させたもの。
http://hosho.ees.hokudai.ac.jp/~kubo/stat/iwanamibook/fig/spatial/m1/model.bug.txt
|
1 2 3 4 5 6 7 8 9 10 11 |
model { for (j in 1:N.site) { Y[j] ~ dpois(mean[j]) log(mean[j]) <- beta + r[j] } r[1:N.site] ~ car.normal(Adj[], Weights[], Num[], tau) beta ~ dnorm(0, 1.0E-4) tau <- 1 / (s * s) s ~ dunif(0, 1.0E+4) } |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
> source("R2WBwrapper.R") # reading "R2WBwrapper.R" (written by kubo@ees.hokudai.ac.jp)... > clear.data.param() > > load("Y.RData") > set.data("N.site", length(Y)) > set.data("Y", Y) > > Adj <- c(sapply(2:(N.site - 1), function(a) c(a - 1, a + 1))) > set.data("Adj", c(2, Adj, N.site - 1)) > set.data("Weights", rep(1, 2 * N.site - 2)) > set.data("Num", c(1, rep(2, N.site - 2), 1)) > > set.param("beta", 0) > set.param("r", rnorm(N.site, 0, 0.1)) > set.param("s", 1) > > post.bugs <- call.bugs( + n.iter = 10100, n.burnin = 100, n.thin = 10 + ) > post.list <- to.list(post.bugs) > post.mcmc <- to.mcmc(post.bugs) |
|
1 |
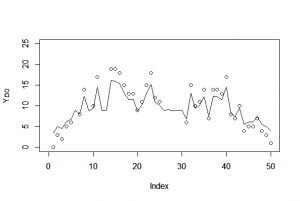
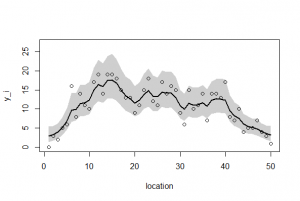
> plot(Y, xlim=c(0,50), ylim=c(0,25)) |
11.2 階層ベイズモデルに空間構造をくみこむ
まずとっかかりとして、個体数yiがすべての区間で共通する平均値λのポアソン分布に従うとする。
データは過分散であり、区画jごとに平均λjが異なっているとする。
平均値λjを線形予測子と対数リンク関数を用いて、
logλj = β + ri
とする。
この線形予測子は、切片β(大域パラメータ)と場所差rj(局所パラメータ)で構成されている。
βには、無情報事前分布を、{rj}には階層事前分布を与える。
11.2.1 空間構造のない階層事前分布
P(rj|s) = 1/√2πs^2exp(-rj^2/2s^2)
11.2.1 空間構造のある階層事前分布
以下の仮定を設ける
区間の場所差は「近傍区間の場所差にしか影響しない
区画jの近傍の個体数njは有限であり、その区画が近傍であるかはモデル設計者が指定する。
近傍の直接の影響はそれも等しく1/nj
さらに簡略化して、この一時空間モデルでは、ある区画はその隣接している区画とだけ相互作用を持つ。
したがって、近傍数njは2で、左右の両端(n1,n50)では1。
p(rj|μj,s) = √(nj/2πs^2exp(-(rj-μj)^2/2s^2/nj)
μj = (rj-1+rj+1)/2、ただし左右の両端j=1とJ=50では、 μ1 = r2, μ50 = r49
このような事前分布は、条件付き自己回帰(conditional auto regressive, CAR)モデルと呼ばれる。
このモデルのようにさまざまの制約をつけて簡単にしたものはintrinsic Gaussian CARモデルと分類される。
この場所差{rj} = {r1,r2,….r50}全体の事前分布である同時分布p){rj}|s)は以下のようになる。
p({rj}|s) ∝ exp(^1/2s^2Σ(rj-rj’)^2
11.3 空間統計モデルをデータにあてはめる
事後分布は、
p(β,s,{rj}|Y) ∝ p({rj}|s)p(s)p(β)Πp(yi|λi)
データyjが得られる確率p(yj|λj)は平均λj=exp(β+rj)のポアソン分布とする。
大域的なパラメータβには、無情報事前分布p(β)を指定する。
局所的なパラメータである場所差rjの事前分布は、空間相関を考慮した階層事前分布として、同時分布p({rj}|s)を使っている。MCMCサンプリングでは、個々のrjの条件付き事前分布p(rj|μ,s)を使用し、これは平均μjで標準偏差s/√njの正規分布、sの事前分布p(s)は無情報事前分布であるとする。
http://hosho.ees.hokudai.ac.jp/~kubo/stat/iwanamibook/fig/spatial/m1/model.bug.txt
|
1 2 3 4 5 6 7 8 9 10 11 |
model { for (j in 1:N.site) { Y[j] ~ dpois(mean[j]) log(mean[j]) <- beta + r[j] } r[1:N.site] ~ car.normal(Adj[], Weights[], Num[], tau) beta ~ dnorm(0, 1.0E-4) tau <- 1 / (s * s) s ~ dunif(0, 1.0E+4) } |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
> load("Y.RData") > set.data("N.site", length(Y)) > set.data("Y", Y) > > Adj <- c(sapply(2:(N.site - 1), function(a) c(a - 1, a + 1))) > set.data("Adj", c(2, Adj, N.site - 1)) > set.data("Weights", rep(1, 2 * N.site - 2)) > set.data("Num", c(1, rep(2, N.site - 2), 1)) > > set.param("beta", 0) > set.param("r", rnorm(N.site, 0, 0.1)) > set.param("s", 1) > > post.bugs <- call.bugs( + n.iter = 10100, n.burnin = 100, n.thin = 10 + ) > post.list <- to.list(post.bugs) > post.mcmc <- to.mcmc(post.bugs) |
|
1 |
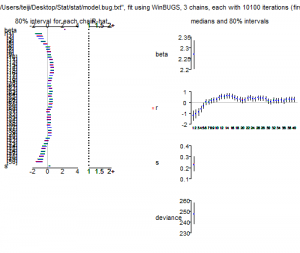
> plot(post.bugs) |
BUGSコードでの注意点は、
r[1:N.site]~car.normal(Adj[], Weights[], Num[], tau)
で、car.normal()関数は、intrinsic Gaussian CARモデルから[rj}のMCMCサンプルを発生させる関数。Adj[]は隣接する場所の番号j、Weights[]はAdj[]に対応する重み、Num[]はそれぞれの区画に隣接する場所の数nj、tauは分散の逆数、つまり1/s^2。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
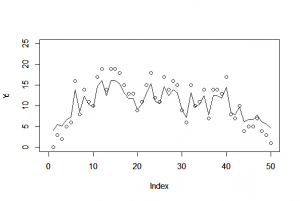
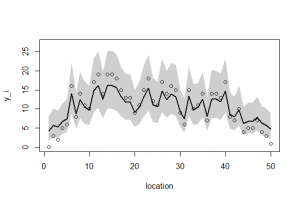
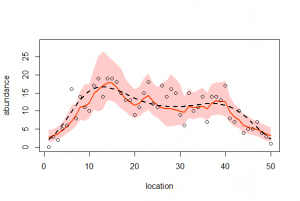
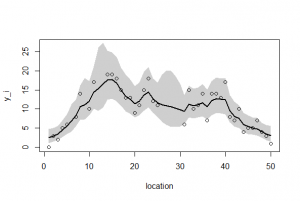
> library(R2WinBUGS) > if (!exists("Y")) load("Y.RData") > if (!exists("post.bugs")) load("post.bugs.RData") > #post.mcmc <- to.mcmc(post.bugs) > post.mcmc <- as.mcmc(post.bugs$sims.matrix) > v <- 1:length(Y) > y.max <- 27 > > plot( + v, Y, + xlab = "location", + ylab = "y_i", + ylim = c(0, y.max) + ) > lines(m, lwd = 2, lty = 2) > > mre <- sapply( + v, function(i) quantile( + post.mcmc[, sprintf("r[%i]", i)], + probs = c(0.5, 0.025, 0.975) + ) + ) > b <- median(post.mcmc[,"beta"]) > polygon( + c(v, rev(v)), + exp(b + c(mre[2,], rev(mre[3,]))), + border = NA, + col = "#00000030" + ) > lines(exp(b + mre[1,]), lwd = 2) |
http://hosho.ees.hokudai.ac.jp/~kubo/stat/iwanamibook/fig/spatial/m2/model.bug.txt
GLMM model の例 (11.2.1 項, 11.5 節)
|
1 2 3 4 5 6 7 8 9 10 11 |
model { for (j in 1:N.site) { Y[j] ~ dpois(mean[j]) log(mean[j]) <- beta + r[j] r[j] ~ dnorm(0.0, tau) } beta ~ dnorm(0, 1.0E-4) tau <- 1 / (s * s) s ~ dunif(0, 1.0E+4) } |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
> source("R2WBwrapper.R") # reading "R2WBwrapper.R" (written by kubo@ees.hokudai.ac.jp)... > clear.data.param() > > load("Y.RData") > set.data("N.site", length(Y)) > set.data("Y", Y) > > set.param("beta", 0) > set.param("r", rnorm(N.site, 0, 0.1)) > set.param("s", 1) > > post.bugs <- call.bugs( + n.iter = 10100, n.burnin = 100, n.thin = 10 + ) > post.list <- to.list(post.bugs) > post.mcmc <- to.mcmc(post.bugs) |
|
1 |
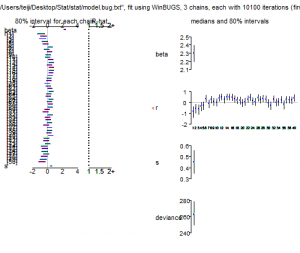
> plot(post.bugs) |
http://hosho.ees.hokudai.ac.jp/~kubo/stat/iwanamibook/fig/spatial/model.bug.txt
> Adj <- c(sapply(2:(N.site - 1), function(a) c(a - 1, a + 1)))
#Adj 隣接する場所の番号:function(a)を2:49繰り返す。
> set.data(“Adj”, c(2, Adj, N.site – 1))
> Adj
[1] 2 1 3 2 4 3 5 4 6 5 7 6 8 7 9 8 10 9 11 10 12 11 13 12 14 13 15 14 16 15
[31] 17 16 18 17 19 18 20 19 21 20 22 21 23 22 24 23 25 24 26 25 27 26 28 27 29 28 30 29 31 30
[61] 32 31 33 32 34 33 35 34 36 35 37 36 38 37 39 38 40 39 41 40 42 41 43 42 44 43 45 44 46 45
[91] 47 46 48 47 49 48 50 49
> set.data(“Weights”, rep(1, 2 * N.site – 2))
#Weights[] は Adj[]に対応する重み
> Weights
[1] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
[47] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
[93] 1 1 1 1 1 1
> set.data(“Num”, c(1, rep(2, N.site – 2), 1))
#Numは、それぞれの区画に隣接する場所の数
> Num
[1] 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
[47] 2 2 2 1
11.4 空間統計モデルが作り出す確率場
隣同士の相互作用をするrjの一次元ならびである{r1,r2,…r50}の関係を決めるために、intrinsic Gaussian CARモデルを部品として用いた。
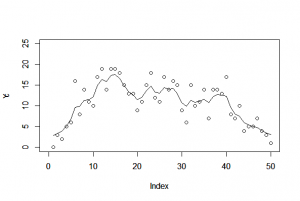
一般に相互作用をする確率変数でうめつくされた空間は確率場random fieldと呼ばれる。ばらつきパラメータsの大小が確率場{rj}にあたえる影響を見ると、大域的なパラメータβを適当に固定して、sを0.0316, 0.224, 10.0とした。sが小さいときは両隣の平均と似た、rj全体のばらつきは小さくなり、sが大きいと全体にぎざぎざしたばらつきの大きい確率場となる。
11.5 空間相関モデルと欠測のある観測データ
空間相関を組み込んだ階層ベイズモデルでは「欠測データ」に対して、より良い予測が得られる。
全部まとめて推定 (欠測あり・なし,CAR と GLMM)
http://hosho.ees.hokudai.ac.jp/~kubo/stat/iwanamibook/fig/spatial/model.bug.txt
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
model { # j = 1: GLMM, no NA data # j = 2: GLMM, NA data # j = 3: CAR, no NA data # j = 4: CAR, NA data Tau.noninformative <- 1.0E-4 S.max <- 1.0E+4 for (i in 1:N.site) { for (j in 1:4) { Y[i, j] ~ dpois(mean [i, j]) log(mean[i, j]) <- beta[j] + r[j, i] } for (j in 1:2) { r[j, i] ~ dnorm(0.0, tau[j]) } } r[3, 1:N.site] ~ car.normal(Adj[], Weights[], Num[], tau[3]) r[4, 1:N.site] ~ car.normal(Adj[], Weights[], Num[], tau[4]) for (j in 1:4) { beta[j] ~ dnorm(0, Tau.noninformative) tau[j] <- 1 / (s[j] * s[j]) s[j] ~ dunif(0, S.max) } } |
全部まとめて推定 (欠測あり・なし,CAR と GLMM)
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
model { # j = 1: GLMM, no NA data GLMM 欠損データなし # j = 2: GLMM, NA data GLMM 欠損データあり # j = 3: CAR, no NA data CAR 欠損データなし # j = 4: CAR, NA data CAR 欠損データあり Tau.noninformative <- 1.0E-4 分散の逆数 Tau=0.0001 S.max <- 1.0E+4 for (i in 1:N.site) { #i=1からi=50まで繰り返す for (j in 1:4) { #j=1からj=4まで繰り返す Y[i, j] ~ dpois(mean [i, j]) #Yはポアソン分布に従う。 log(mean[i, j]) <- beta[j] + r[j, i] #log(λ)=β + r[i] } for (j in 1:2) { #j=1からj=2繰り返す r[j, i] ~ dnorm(0.0, tau[j]) r[j,i]は正規分布N(0,分散の逆数) } } r[3, 1:N.site] ~ car.normal(Adj[], Weights[], Num[], tau[3]) #r[3]について r[4, 1:N.site] ~ car.normal(Adj[], Weights[], Num[], tau[4]) #r[4]について for (j in 1:4) { j=1からj=4まで繰り返す beta[j] ~ dnorm(0, Tau.noninformative) #βは正規分布N(0, 100) tau[j] <- 1 / (s[j] * s[j]) #tauは、分散の逆数 s[j] ~ dunif(0, S.max) #sには一様分布 } } |
post.bugsには、4種類(欠損なしGLMM、欠損ありGLMM、欠損なしCarモデル、欠損ありCarモデル)の分析結果βとr[i]が含まれている。
それぞれを順番に取り出して、λi = exp(β + ri)を計算する。
Yに対して欠損データYnoを作成するためのコードを以下に示す。
http://hosho.ees.hokudai.ac.jp/~kubo/stat/iwanamibook/fig/spatial/set.data.R
|
1 2 3 4 5 6 7 8 9 10 11 12 |
> source("R2WBwrapper.R") # reading "R2WBwrapper.R" (written by kubo@ees.hokudai.ac.jp)... > clear.data.param() > > load("Y.RData") > no <- c(6, 9, 12, 13, 26:30) #欠損データ番号をnoで指定する。 > Yno <- Y #データYをYnoへ > Yno[no] <- NA #Ynoの[no]の位置をNA(欠損)とする。 > > set.data("N.site", length(Y)) #N.siteはYの数、ここでは50 > set.data("Y", matrix(c(Y, Yno, Y, Yno), N.site, 4)) #欠損なし、欠損あり、欠損なし、欠損ありのデータYを行列Yに |
欠損データあるなし、およびGLMMもしくはCarモデルの通りを上記BUGSモデルと、欠損データを作成するRを読み込んで、以下のように実行する。
http://hosho.ees.hokudai.ac.jp/~kubo/stat/iwanamibook/fig/spatial/runbugs.R
|
1 2 3 4 5 6 7 8 9 |
source("set.data.R") #set.data.Rを実行 set.param("beta", rep(0, 4)) #betaに{0,0,0,0} set.param("r", matrix(rnorm(N.site * 4, 0, 0.1), 4, N.site)) set.param("s", rep(1, 4))#sに{1,1,1,1} post.bugs <- call.bugs(n.iter = 10100, n.burnin = 100, n.thin = 10) post.list <- to.list(post.bugs) post.mcmc <- to.mcmc(post.bugs) |
ここでは、
post.bugs <- call.bugs(n.iter = 10100, n.burnin = 100, n.thin = 10)
で指定されているように、10100回のサンプリング、burn-inの100回、10個ごとの間引きで、1ループで1000個のデータが生成される。デフォルトで3ループ繰り返されるので、3000データが生成されて、post.listには1000個づつx3ループ、post.mcmcには3000行のデータxパラメータ数列となる。
|
1 |
> plot(post.bugs) |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
> post.bugs_mean$mean$r[,1] [1] -0.8772744 -0.9358953 -1.2306306 -1.2986994 > post.bugs_mean$mean$r[1,] [1] -0.877274390 -0.580566031 -0.656468680 -0.407739569 -0.306295546 0.338722675 -0.146676731 [8] 0.220952620 0.047631339 -0.021084334 0.394721414 0.483332087 0.229919000 0.484071168 [15] 0.485096545 0.438500246 0.282078789 0.166599136 0.168884978 -0.081065916 0.049102031 [22] 0.282005874 0.439967327 0.111860874 0.056472169 0.390653565 0.227011052 0.337832611 [29] 0.288428335 -0.079034864 -0.310339911 0.288413285 -0.007770132 0.047258392 0.228505448 [36] -0.232892552 0.231891357 0.229222556 0.177950440 0.383802796 -0.154800235 -0.232420948 [43] -0.014877777 -0.480295044 -0.393010223 -0.388169258 -0.239045123 -0.475872859 -0.569454256 [50] -0.761291851 > post.bugs_mean$mean$beta[1] [1] 2.295042 |
|
1 2 3 4 5 6 |
> a + b [1] 1.417768 1.714476 1.638573 1.887302 1.988746 2.633765 2.148365 2.515995 2.342673 2.273958 [11] 2.689763 2.778374 2.524961 2.779113 2.780139 2.733542 2.577121 2.461641 2.463927 2.213976 [21] 2.344144 2.577048 2.735009 2.406903 2.351514 2.685696 2.522053 2.632875 2.583470 2.216007 [31] 1.984702 2.583455 2.287272 2.342300 2.523547 2.062149 2.526933 2.524265 2.472992 2.678845 [41] 2.140242 2.062621 2.280164 1.814747 1.902032 1.906873 2.055997 1.819169 1.725588 1.533750 |
|
1 2 3 4 5 6 7 8 |
> c <-exp(a+b) > c [1] 4.127895 5.553764 5.147820 6.601537 7.306369 13.926099 8.570836 12.378915 10.409026 [10] 9.717785 14.728191 16.092834 12.490408 16.104732 16.121254 15.387296 13.159195 11.724036 [19] 11.750866 9.152033 10.424346 13.158236 15.409887 11.099531 10.501459 14.668401 12.454139 [28] 13.913709 13.243016 9.170641 7.276879 13.242817 9.848034 10.405145 12.472765 7.862852 [37] 12.515068 12.481712 11.857878 14.568254 8.501493 7.866561 9.778286 6.139522 6.699493 [46] 6.732003 7.814624 6.166733 5.615821 4.635528 |
ここで注意点はpost.mcmcのデータ構造
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 |
> post.mcmc Markov Chain Monte Carlo (MCMC) output: Start = 1 End = 3000 Thinning interval = 1 beta[1] beta[2] beta[3] beta[4] r[1,1] r[1,2] r[1,3] r[1,4] r[1,5] [1,] 2.294 2.051 2.193 2.192 -0.184000 -1.871e-01 -0.542600 -0.6605000 -0.3922000 [2,] 2.316 2.370 2.305 2.267 -0.675000 -3.813e-01 -0.661100 -0.4455000 -0.7130000 [3,] 2.195 2.190 2.329 2.311 -1.422000 -7.148e-01 -0.531800 -0.5550000 -0.4738000 [4,] 2.298 2.235 2.232 2.172 -0.504500 -7.125e-01 -0.829200 -0.5473000 -0.2860000 r[1,6] r[1,7] r[1,8] r[1,9] r[1,10] r[1,11] r[1,12] r[1,13] [1,] 0.0867300 -6.503e-02 -0.0742600 0.1154000 -0.0500900 5.414e-01 0.4563000 -2.418e-01 [2,] 0.0760800 -1.326e-01 0.1549000 0.5488000 0.1010000 1.857e-01 0.5511000 4.640e-01 [3,] 0.3349000 -3.765e-01 -0.2056000 0.1575000 0.5661000 9.113e-01 0.5946000 5.373e-01 [4,] 0.5667000 -7.593e-01 0.5229000 -0.1659000 0.0539500 3.522e-01 0.8624000 1.665e-01 r[1,14] r[1,15] r[1,16] r[1,17] r[1,18] r[1,19] r[1,20] r[1,21] [1,] 0.749800 0.0333100 0.598800 0.0871900 0.2788000 3.107e-01 1.803e-01 0.1775000 [2,] 0.681400 0.8370000 0.357800 0.2257000 0.1258000 3.189e-01 4.315e-02 0.1833000 [3,] 0.768700 0.7005000 0.361600 -0.3429000 0.1172000 2.172e-01 4.955e-01 0.5567000 [4,] 0.346100 0.7671000 0.523200 -0.0166700 0.3641000 -7.296e-02 1.253e-01 -0.0680100 r[1,22] r[1,23] r[1,24] r[1,25] r[1,26] r[1,27] r[1,28] r[1,29] [1,] 0.0779800 0.3184000 0.1885000 0.2936000 3.396e-01 0.1845000 0.0166300 1.203e-01 [2,] 0.5982000 0.4894000 0.3473000 -0.3248000 3.938e-01 0.1577000 0.2843000 1.501e-01 [3,] 0.3063000 0.0815500 -0.4000000 -0.2463000 7.607e-01 0.4773000 0.5573000 5.633e-01 [4,] 0.3005000 0.4725000 0.3624000 -0.2298000 6.308e-01 0.3169000 0.4298000 5.019e-01 r[1,30] r[1,31] r[1,32] r[1,33] r[1,34] r[1,35] r[1,36] r[1,37] [1,] -9.904e-02 -0.1424000 3.267e-01 0.3049000 0.2157000 -0.0728600 -1.163e-01 5.424e-01 [2,] 4.082e-01 -0.3721000 1.797e-01 -0.3569000 0.0355100 0.5272000 2.062e-01 2.491e-01 [3,] 4.691e-01 0.4145000 1.891e-01 0.0060420 0.6449000 0.7702000 -1.952e-01 3.466e-01 [4,] -7.298e-01 -0.2007000 1.658e-01 0.1697000 0.5791000 0.1914000 1.886e-01 1.043e-01 r[1,38] r[1,39] r[1,40] r[1,41] r[1,42] r[1,43] r[1,44] r[1,45] [1,] 5.335e-01 2.031e-01 0.5186000 -0.3686000 -0.6094000 0.1413000 -0.6070000 -0.7182000 [2,] 5.382e-01 1.626e-01 0.3037000 0.2069000 -0.6284000 0.2288000 -0.3483000 -0.4521000 [3,] 3.967e-01 5.049e-01 0.4727000 -0.1241000 -0.0732200 0.0543400 0.1101000 -0.5163000 [4,] 2.606e-01 1.974e-01 0.2680000 -0.3847000 -0.1880000 0.3385000 -0.8183000 -0.1406000 r[1,46] r[1,47] r[1,48] r[1,49] r[1,50] r[2,1] r[2,2] r[2,3] [1,] -4.651e-01 -3.153e-02 -6.768e-01 -0.5641000 -0.3794000 -1.067000 -0.0100600 -0.4763000 [2,] -1.775e-01 -4.655e-01 -2.462e-01 -0.7910000 -1.4160000 -1.096000 -1.2670000 -0.4688000 [3,] -2.322e-01 -5.242e-01 -1.242e+00 -1.2730000 -0.9799000 -1.746000 -1.5460000 -1.2640000 [4,] -2.316e-01 -1.174e-01 -8.011e-01 -0.6913000 -1.1240000 -0.857500 0.1322000 -0.5922000 r[2,4] r[2,5] r[2,6] r[2,7] r[2,8] r[2,9] r[2,10] r[2,11] [1,] -0.1820000 -5.423e-01 -0.9179000 3.992e-01 0.6138000 0.0237600 -0.1426000 0.158600 [2,] -0.6408000 -7.022e-01 -0.4431000 -2.470e-01 -0.1630000 0.7988000 -0.0087020 0.278400 [3,] -0.6576000 -7.064e-01 0.9225000 8.755e-03 0.0159900 0.3184000 0.4216000 0.585400 [4,] -0.2565000 -1.817e-01 -0.2752000 -6.252e-02 0.1774000 0.5457000 0.1073000 0.491200 r[2,12] r[2,13] r[2,14] r[2,15] r[2,16] r[2,17] r[2,18] r[2,19] [1,] 0.2646000 -7.531e-01 0.6017000 0.887100 0.492200 0.2084000 0.1451000 0.5046000 [2,] 1.0590000 -6.578e-01 0.3553000 -0.013350 0.485400 0.1785000 -0.1449000 0.3871000 [3,] 1.9070000 9.348e-02 0.5979000 0.472300 0.880600 0.3059000 0.5433000 0.4471000 [4,] 0.1177000 6.229e-01 0.4983000 0.298900 0.301000 0.4339000 0.3085000 0.1576000 r[2,20] r[2,21] r[2,22] r[2,23] r[2,24] r[2,25] r[2,26] r[2,27] [1,] -0.1526000 0.4064000 0.7253000 0.836100 0.2735000 0.7314000 -0.0729000 0.2756000 [2,] -0.3102000 -0.2268000 -0.1055000 0.342000 0.0665000 0.4495000 0.0216700 -0.0185100 [3,] -0.0180800 -0.0703800 0.5230000 0.575800 0.1699000 0.0830900 0.8049000 0.3380000 [4,] 0.0423800 0.1806000 0.0860000 0.397600 0.2460000 0.1646000 -0.4247000 -0.5344000 r[2,28] r[2,29] r[2,30] r[2,31] r[2,32] r[2,33] r[2,34] r[2,35] [1,] -6.273e-01 1.099e+00 -0.8262000 -0.1396000 6.239e-01 2.443e-01 5.053e-01 4.794e-01 [2,] 7.327e-01 -5.548e-02 -1.0520000 -0.4759000 3.361e-01 -2.064e-01 -1.881e-01 4.027e-01 [3,] 9.410e-01 -1.031e-01 -0.4448000 -0.3993000 6.832e-01 3.885e-01 1.407e-01 -4.581e-02 [4,] 3.223e-01 -5.821e-01 0.3541000 -0.3811000 4.329e-01 1.266e-01 1.426e-02 4.436e-01 r[2,36] r[2,37] r[2,38] r[2,39] r[2,40] r[2,41] r[2,42] r[2,43] [1,] -0.3764000 0.233000 -0.0742900 0.3469000 0.4931000 -2.561e-01 0.1880000 9.021e-02 [2,] 0.0116900 0.380300 0.1019000 -0.0423200 0.4689000 -1.823e-01 0.2037000 -3.014e-01 [3,] -0.1887000 0.412500 0.1803000 0.1614000 0.2131000 3.023e-01 -0.1203000 -4.850e-01 [4,] -0.2095000 0.276300 0.6309000 0.2329000 0.5323000 -1.483e-01 -0.2390000 2.891e-01 r[2,44] r[2,45] r[2,46] r[2,47] r[2,48] r[2,49] r[2,50] r[3,1] [1,] -0.6789000 -0.3418000 -1.922e-01 7.442e-02 -6.422e-01 -0.7425000 -1.420000 -1.3740 [2,] -0.8614000 -1.1650000 -5.088e-01 -5.693e-01 -8.843e-01 -0.7517000 -0.334400 -0.6008 [3,] -1.2550000 -0.7209000 -3.944e-01 -5.966e-01 -6.926e-01 -0.5352000 -0.806300 -1.6590 [4,] -0.6016000 -0.0281900 -4.100e-01 8.506e-02 -1.340e-01 -0.6955000 -0.529600 -1.2910 r[3,2] r[3,3] r[3,4] r[3,5] r[3,6] r[3,7] r[3,8] r[3,9] [1,] -0.8412 -0.7736 -0.44490 -0.1799000 5.350e-03 -0.1829000 -0.0663000 2.610e-01 [2,] -0.7280 -0.5319 -0.33190 0.1591000 2.057e-01 0.1008000 0.4104000 3.407e-01 [3,] -1.0940 -1.0400 -0.74240 -0.3556000 2.081e-01 0.2906000 0.2971000 3.235e-01 [4,] -1.3680 -1.6580 -0.84860 -0.2674000 6.032e-02 0.2968000 0.2196000 2.653e-01 r[3,10] r[3,11] r[3,12] r[3,13] r[3,14] r[3,15] r[3,16] r[3,17] [1,] 1.834e-01 0.2834000 0.8431000 0.857900 0.71420 0.8814 0.803600 0.6784000 [2,] 1.490e-01 0.5246000 0.5679000 0.488800 0.49880 0.5580 0.557100 0.3027000 [3,] 1.211e-02 0.5877000 0.7967000 0.493400 0.68570 0.8079 0.936900 0.4495000 [4,] 2.984e-01 0.4289000 0.2854000 0.544100 0.48940 0.5797 0.498600 0.3108000 r[3,18] r[3,19] r[3,20] r[3,21] r[3,22] r[3,23] r[3,24] r[3,25] [1,] 0.4361000 0.2875000 0.2016000 0.1761000 0.293400 0.145400 0.0073350 0.1917000 [2,] -0.0791800 0.0186000 0.0894100 0.2427000 0.287700 0.431500 0.3116000 0.3072000 [3,] 0.1595000 0.0698900 0.1023000 0.3592000 0.195800 0.056170 0.2333000 0.2630000 [4,] 0.3401000 0.5616000 0.3584000 0.3111000 0.247100 0.420300 0.2898000 0.4322000 r[3,26] r[3,27] r[3,28] r[3,29] r[3,30] r[3,31] r[3,32] r[3,33] [1,] 0.1448000 0.2828000 0.426100 5.175e-01 0.3974000 0.2293000 2.421e-01 2.280e-01 [2,] 0.3187000 0.4894000 0.349000 2.304e-01 0.2025000 0.2534000 2.369e-01 1.390e-01 [3,] 0.7321000 0.7698000 0.370700 1.609e-01 0.0458500 -0.0672800 -2.328e-01 -1.195e-01 [4,] 0.7638000 0.5596000 0.317200 3.770e-01 -0.1905000 -0.0954900 2.724e-01 -3.919e-02 r[3,34] r[3,35] r[3,36] r[3,37] r[3,38] r[3,39] r[3,40] r[3,41] [1,] 2.398e-01 -0.0201000 0.0810900 0.1590000 0.3012000 0.2942000 0.1397000 -9.223e-02 [2,] 5.293e-02 -0.0803800 0.1154000 0.0705100 -0.0272300 -0.0172600 -0.0548400 -2.279e-01 [3,] -6.026e-02 0.5138000 0.2364000 0.3077000 0.4261000 0.2168000 0.0103100 1.341e-01 [4,] 4.769e-01 0.7058000 0.3803000 0.4335000 0.1008000 0.0798400 0.2456000 -1.648e-02 r[3,42] r[3,43] r[3,44] r[3,45] r[3,46] r[3,47] r[3,48] r[3,49] r[3,50] [1,] -0.1748000 -0.4660000 -0.436100 -0.611600 -0.86660 -0.93210 -0.9658 -1.1880 -1.3180 [2,] -0.2461000 -0.4248000 -0.673200 -0.551000 -0.90020 -0.77770 -0.8461 -0.9634 -0.9485 [3,] -0.0431600 -0.1187000 -0.413300 -0.241400 -0.83480 -0.91460 -1.1580 -1.0630 -1.0960 [4,] -0.0587800 -0.1127000 -0.312900 -0.688400 -0.76670 -0.50330 -1.2330 -1.4150 -1.0850 r[4,1] r[4,2] r[4,3] r[4,4] r[4,5] r[4,6] r[4,7] r[4,8] [1,] -1.61600 -1.4870 -0.8721 -0.56790 -0.5224000 0.2979000 9.771e-02 0.0849400 [2,] -1.05200 -0.8342 -0.7451 -0.64850 -0.7761000 -0.3412000 -2.332e-01 0.0908200 [3,] -1.10600 -0.7664 -0.7939 -0.49030 -0.5135000 -0.4692000 -2.625e-01 -0.0209900 [4,] -1.33700 -1.2860 -0.8053 -0.64510 -0.4482000 -0.5345000 -2.910e-01 0.2586000 r[4,9] r[4,10] r[4,11] r[4,12] r[4,13] r[4,14] r[4,15] r[4,16] [1,] 1.549e-01 0.0883100 0.592700 0.721500 0.6315000 0.76400 0.72530 0.542400 [2,] 4.697e-02 0.3291000 0.710600 0.725400 0.6763000 0.81740 0.49740 0.560500 [3,] 5.355e-02 0.1794000 0.223200 0.168700 0.4130000 0.35040 0.30680 0.365800 [4,] 3.239e-01 0.3608000 0.619200 0.162100 0.4902000 0.49280 0.47710 0.205300 r[4,17] r[4,18] r[4,19] r[4,20] r[4,21] r[4,22] r[4,23] r[4,24] [1,] 0.462100 0.6292000 0.5925000 9.198e-02 0.2830000 0.492700 0.606600 0.1690000 [2,] 0.524200 0.2001000 0.3273000 7.474e-02 0.0279900 0.197500 0.328600 0.2379000 [3,] 0.422100 0.2120000 0.3146000 4.772e-01 0.5383000 0.460800 0.556900 0.5039000 [4,] 0.306900 0.1946000 0.4208000 4.613e-01 0.5949000 0.785500 0.816000 0.5732000 r[4,25] r[4,26] r[4,27] r[4,28] r[4,29] r[4,30] r[4,31] r[4,32] [1,] 0.4290000 0.4631000 0.7194000 0.2983000 0.0834600 -0.0293200 -0.0190800 0.2411000 [2,] -0.0011050 0.1949000 0.1906000 0.1803000 -0.3705000 -0.0998000 -0.0156200 -0.0135000 [3,] 0.3810000 0.5111000 0.4947000 0.3919000 0.2019000 0.1183000 -0.0355300 0.0035930 [4,] 0.3388000 0.3502000 0.2177000 0.3561000 0.3852000 -0.0298600 0.2068000 0.1602000 r[4,33] r[4,34] r[4,35] r[4,36] r[4,37] r[4,38] r[4,39] r[4,40] [1,] 2.927e-01 0.5378000 0.4835000 1.904e-01 0.2361000 0.380300 0.3410000 0.3653000 [2,] 1.416e-01 0.2387000 -0.0140800 1.697e-01 0.2737000 0.362200 0.2003000 0.1528000 [3,] -1.224e-01 0.1920000 0.1961000 2.080e-01 0.1037000 0.027550 0.1119000 0.0011790 [4,] -9.594e-02 -0.1328000 0.0845600 3.937e-02 0.1651000 0.224600 0.1937000 0.3148000 r[4,41] r[4,42] r[4,43] r[4,44] r[4,45] r[4,46] r[4,47] r[4,48] [1,] -2.183e-02 -5.549e-01 -7.060e-01 -0.6123000 -0.593000 -0.685200 -0.966400 -1.08200 [2,] 6.424e-02 9.501e-02 1.667e-01 -0.1839000 -0.272200 -0.347300 -0.344400 -0.59630 [3,] -1.468e-01 -2.006e-02 -8.554e-02 -0.2218000 -0.304000 -0.488800 -0.579300 -0.58250 [4,] 1.281e-01 1.790e-01 -2.329e-01 -0.2814000 -0.326100 -0.624200 -0.602400 -0.92500 r[4,49] r[4,50] s[1] s[2] s[3] s[4] deviance [1,] -1.21200 -1.5410 0.3855 0.5610 0.23300 0.2466 915.9 [2,] -0.96880 -0.9461 0.4512 0.6514 0.18260 0.2015 916.8 [3,] -0.65610 -0.8237 0.5136 0.5762 0.27390 0.1280 927.5 [4,] -1.05000 -1.2400 0.5559 0.3875 0.29680 0.2200 902.2 [ reached getOption("max.print") -- omitted 2996 rows ] > |
つまり、上記のようにβ[1]からβ[4],r[i,j], s[1]からs[4]までが、[1,]から[4,]行で表示されている。実際には[ reached getOption(“max.print”) — omitted 2996 rows ]とされているように3000行ある。
もともとMCMCでは、
post.bugs <- call.bugs(n.iter = 10100, n.burnin = 100, n.thin = 10)
でpost.bugsが生成されているので、burn-inが100回、MCMCのサンプリングが10100回で、burn-inの100回を除くと10000回。それをn.thinで10回に一回の間引きすると一回のループで1000個のデータが得られる。さらにdefaultで3回回転させるので、データ量は1ループで1000個、3ループで3000個となる。
よって、post.mcmcには3000行、post.listは3ループ、それぞれ1000行のサンプルとなる。
以下のプログラムを参考:
|
1 2 3 4 5 6 |
mre <- sapply( v, function(i) quantile( post.mcmc[,<strong> sprintf("r[%i]"</strong>, i)], probs = c(0.5, 0.025, 0.975) ) ) |
post.mcmcのr[i]のデータからquantile()関数を用いて、mre[1]に中位点、mre[2]に2.5%位点、mre[3]に97.5%位点を求めている。 今回の分析では、4つの異なる条件(欠損データあるなし、GLMMかCarモデルか)がまとめてpost.bugsに収められており、個体差のデータr[i]も二次元r[j,i]となっているために"r[%i]"を"r[j,%i]とする。また欠損なしのデータYに対して、欠損ありデータYnoを指定し、またパラメータbetaには、beta[1]?beta[4]を指定する。 http://hosho.ees.hokudai.ac.jp/~kubo/stat/iwanamibook/fig/spatial/m1/fig11_04.R
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
library(R2WinBUGS) if (!exists("Y")) load("Y.RData") if (!exists("post.bugs")) load("post.bugs.RData") #post.mcmc <- to.mcmc(post.bugs) post.mcmc <- as.mcmc(post.bugs$sims.matrix) v <- 1:length(Y) y.max <- 27 plot( v, Y, xlab = "location", ylab = "y_i", ylim = c(0, y.max) ) lines(m, lwd = 2, lty = 2) mre <- sapply( v, function(i) quantile( post.mcmc[, sprintf("r[%i]", i)], probs = c(0.5, 0.025, 0.975) ) ) b <- median(post.mcmc[,"beta"]) polygon( c(v, rev(v)), exp(b + c(mre[2,], rev(mre[3,]))), border = NA, col = "#00000030" ) lines(exp(b + mre[1,]), lwd = 2) |
上記プログラムの3箇所:
?plot(
v, Y,
xlab = “location”,
ylab = “y_i”,
ylim = c(0, y.max)
)
1.Y
2.Yno
3.Y
4.Yno
?v, function(i) quantile(
post.mcmc[, sprintf(“r[%i]“, i)],
probs = c(0.5, 0.025, 0.975)
)
1.r[%i]をr[1,%i]
2.r[%i]をr[2,%i]
3.r[%i]をr[3,%i]
4.r[%i]をr[4,%i]
?b <- median(post.mcmc[,"beta“])
1. betaをbeta[1]
2. betaをbeta[2]
3. betaをbeta[3]
4. betaをbeta[4]
> post.mcmc[, sprintf(“r[1,%i]”, 1)]
Markov Chain Monte Carlo (MCMC) output:
Start = 1
End = 3000
Thinning interval = 1
[1] -0.18400 -0.67500 -1.42200 -0.50450 -0.63360 -1.10700 -0.35370 -0.83640 -1.30700 -0.98050
[11] -1.26100 -0.72610 -0.86080 -0.90290 -0.39940 -0.86940 -0.34790 -0.76790 -1.27100 -0.80690
[21] -0.98250 -0.70730 -1.56600 -1.41300 -0.92780 -0.18960 -0.75360 -0.75330 -0.88030 -1.12000
……
[981] -0.63590 -0.89070 -0.57660 -1.04800 -0.38740 -0.61560 -1.01800 -0.63090 -0.70580 -0.41810
[991] -1.13800 -0.62850 -0.70830 -0.29860 -0.92840 -1.29800 -0.36910 -1.56400 -0.84220 -0.97500
[ reached getOption(“max.print”) — omitted 2000 entries ]
1. 欠損なし、GLMMモデル
|
1 2 3 4 5 6 7 8 |
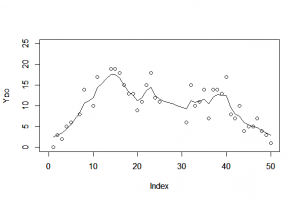
> plot(Y, xlim=c(0,50), ylim=c(0,25)) Hit <Return> to see next plot: > par(new=T) > plot(c, type="l") > plot(Y, xlim=c(0,50), ylim=c(0,25)) Hit <Return> to see next plot: > par(new=T) > plot(c, xlim=c(0,50), ylim=c(0,25), type="l") |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
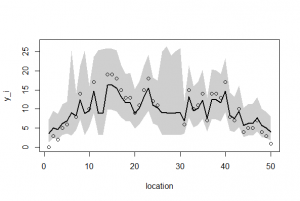
> library(R2WinBUGS) > if (!exists("Y")) load("Y.RData") > if (!exists("post.bugs")) load("post.bugs.RData") > #post.mcmc <- to.mcmc(post.bugs) > post.mcmc <- as.mcmc(post.bugs$sims.matrix) > v <- 1:length(Y) > y.max <- 27 > > plot( + v, Y, + xlab = "location", + ylab = "y_i", + ylim = c(0, y.max) + ) Hit <Return> to see next plot: lines(m, lwd = 2, lty = 2) > > mre <- sapply( + v, function(i) quantile( + post.mcmc[, sprintf("r[1,%i]", i)], + probs = c(0.5, 0.025, 0.975) + ) + ) > b <- median(post.mcmc[,"beta[1]"]) > polygon( + c(v, rev(v)), + exp(b + c(mre[2,], rev(mre[3,]))), + border = NA, + col = "#00000030" + ) > lines(exp(b + mre[1,]), lwd = 2) |
2.欠損あり、GLMMモデル
|
1 2 3 4 5 6 7 8 9 10 11 |
> a <- post.bugs_mean$mean$beta[2] > b <- post.bugs_mean$mean$r[2,] > c <-exp(a+b) > plot(Y, xlim=c(0,50), ylim=c(0,25)) Hit <Return> to see next plot: > par(new=T) > plot(c, xlim=c(0,50), ylim=c(0,25), type="l") > plot(Yno, xlim=c(0,50), ylim=c(0,25)) Hit <Return> to see next plot: > par(new=T) > plot(c, xlim=c(0,50), ylim=c(0,25), type="l") |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
> library(R2WinBUGS) > if (!exists("Y")) load("Y.RData") > if (!exists("post.bugs")) load("post.bugs.RData") > #post.mcmc <- to.mcmc(post.bugs) > post.mcmc <- as.mcmc(post.bugs$sims.matrix) > v <- 1:length(Y) > y.max <- 27 > > plot( + v, Yno, + xlab = "location", + ylab = "y_i", + ylim = c(0, y.max) + ) Hit <Return> to see next plot: lines(m, lwd = 2, lty = 2) > > mre <- sapply( + v, function(i) quantile( + post.mcmc[, sprintf("r[2,%i]", i)], + probs = c(0.5, 0.025, 0.975) + ) + ) > b <- median(post.mcmc[,"beta[2]"]) > polygon( + c(v, rev(v)), + exp(b + c(mre[2,], rev(mre[3,]))), + border = NA, + col = "#00000030" + ) > lines(exp(b + mre[1,]), lwd = 2) |
|
1 2 3 4 5 6 7 |
> a <- post.bugs_mean$mean$beta[3] > b <- post.bugs_mean$mean$r[3,] > c <-exp(a+b) > plot(Y, xlim=c(0,50), ylim=c(0,25)) Hit <Return> to see next plot: > par(new=T) > plot(c, xlim=c(0,50), ylim=c(0,25), type="l") |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
> library(R2WinBUGS) > if (!exists("Y")) load("Y.RData") > if (!exists("post.bugs")) load("post.bugs.RData") > #post.mcmc <- to.mcmc(post.bugs) > post.mcmc <- as.mcmc(post.bugs$sims.matrix) > v <- 1:length(Y) > y.max <- 27 > > plot( + v, Y, + xlab = "location", + ylab = "y_i", + ylim = c(0, y.max) + ) Hit <Return> to see next plot: lines(m, lwd = 2, lty = 2) > > mre <- sapply( + v, function(i) quantile( + post.mcmc[, sprintf("r[3,%i]", i)], + probs = c(0.5, 0.025, 0.975) + ) + ) > b <- median(post.mcmc[,"beta[3]"]) > polygon( + c(v, rev(v)), + exp(b + c(mre[2,], rev(mre[3,]))), + border = NA, + col = "#00000030" + ) > lines(exp(b + mre[1,]), lwd = 2) |
|
1 2 3 4 5 6 7 |
> a <- post.bugs_mean$mean$beta[4] > b <- post.bugs_mean$mean$r[4,] > c <-exp(a+b) > plot(Yno, xlim=c(0,50), ylim=c(0,25)) Hit <Return> to see next plot: > par(new=T) > plot(c, xlim=c(0,50), ylim=c(0,25), type="l") |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
> library(R2WinBUGS) > if (!exists("Y")) load("Y.RData") > if (!exists("post.bugs")) load("post.bugs.RData") > #post.mcmc <- to.mcmc(post.bugs) > post.mcmc <- as.mcmc(post.bugs$sims.matrix) > v <- 1:length(Y) > y.max <- 27 > > plot( + v, Yno, + xlab = "location", + ylab = "y_i", + ylim = c(0, y.max) + ) Hit <Return> to see next plot: lines(m, lwd = 2, lty = 2) > > mre <- sapply( + v, function(i) quantile( + post.mcmc[, sprintf("r[4,%i]", i)], + probs = c(0.5, 0.025, 0.975) + ) + ) > b <- median(post.mcmc[,"beta[4]"]) > polygon( + c(v, rev(v)), + exp(b + c(mre[2,], rev(mre[4,]))), + border = NA, + col = "#00000030" + ) > lines(exp(b + mre[1,]), lwd = 2) |
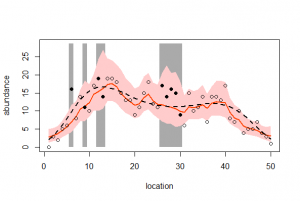
—————————
http://hosho.ees.hokudai.ac.jp/~kubo/ce/2008/car/model1.bug.txt
|
1 2 |
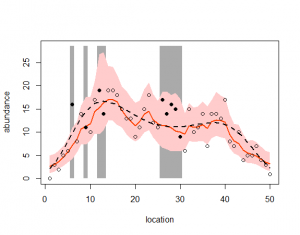
> source("plotcar.R") > plotcar(post.bugs2,v.na=v.na) |
以下、ウェブサイトを参考に動かしてみた。
モデルは
http://hosho.ees.hokudai.ac.jp/~kubo/ce/2008/car/model1.bug.txt
model
{
Tau.noninformative <- 1.0E-2
P.gamma <- 1.0E-2
for (i in 1:N.site) {
Y[i] ~ dpois(mean[i])
log(mean[i]) <- beta + re[i]
}
re[1:N.site] ~ car.normal(Adj[], Weights[], Num[], tau)
beta ~ dnorm(0, Tau.noninformative)
tau ~ dgamma(P.gamma, P.gamma)
}
http://hosho.ees.hokudai.ac.jp/~kubo/ce/2008/car/runbugs2.R
source(“R2WBwrapper.R”)
clear.data.param() # for initialization
# set data
load(“Y.RData”)
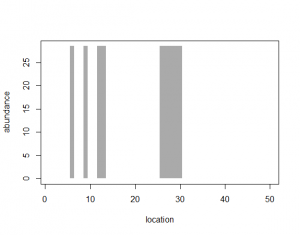
v.na <- c(6, 9, 12, 13, 26:30)
YwithNA <- Y
YwithNA[v.na] <- NA
set.data("N.site", length(YwithNA))
set.data("Y", YwithNA)
Adj <- c(sapply(2:(N.site - 1), function(a) c(a - 1, a + 1)))
set.data("Adj", c(2, Adj, N.site - 1))
set.data("Weights", rep(1, 2 * N.site - 2))
set.data("Num", c(1, rep(2, N.site - 2), 1))
# set parameter
set.param("beta", 0)
set.param("re", rnorm(N.site, 0, 0.1))
set.param("tau", 1)
post.bugs2 <- call.bugs(
file.bug = "model1.bug.txt",
n.iter = 300, n.burnin = 100, n.thin = 1
)
> source(“R2WBwrapper.R”)
# reading “R2WBwrapper.R” (written by kubo@ees.hokudai.ac.jp)…
> clear.data.param() # for initialization
>
> # set data
> load(“Y.RData”)
>
> v.na <- c(6, 9, 12, 13, 26:30)
> YwithNA <- Y
> YwithNA[v.na] <- NA
>
> set.data(“N.site”, length(YwithNA))
> set.data(“Y”, YwithNA)
>
> Adj <- c(sapply(2:(N.site - 1), function(a) c(a - 1, a + 1)))
> set.data(“Adj”, c(2, Adj, N.site – 1))
> set.data(“Weights”, rep(1, 2 * N.site – 2))
> set.data(“Num”, c(1, rep(2, N.site – 2), 1))
>
> # set parameter
> set.param(“beta”, 0)
> set.param(“re”, rnorm(N.site, 0, 0.1))
> set.param(“tau”, 1)
>
> post.bugs2 <- call.bugs(
+ file = "model1.bug.txt", #.bugを外す。
+ n.iter = 300, n.burnin = 100, n.thin = 1
+ )
> source(“plotcar.R”)
# reading “R2WBwrapper.R” (written by kubo@ees.hokudai.ac.jp)…
> plotcar(post.bugs2,v.na=v.na)
Hit
11.6 この章のまとめ
空間構造のあるデータを統計モデル化する場合、近傍とは似ているけれど遠方とは似ていないといった空間相関を考慮しなければならない。
空間相関のある場所差を生成するintrinsic Gaussian CARモデルはWinBUGSで簡単に扱える。
空間相関のある場所差は確率場を使って表現できる
空間相関を考慮した階層ベイズモデルでは、観測データの欠損部分をよそくするような用途にも使える。