ここまで約1ヶ月間、集中的にベイズ統計について学習した。理解できたこととできていないことなど、未だ混沌としているが、「確率と情報の科学:データ解析のための統計モデリング入門(岩波書店、久保拓弥著)を中心に学習したことについて、これまでの知識も交えて以下に整理しておく。
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
第1章 ベイズ定理
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
ベイズ統計学は、1700年代にイギリスの牧師トーマス・ベイズにより発見されたという「ベイズの定理」に基づく。「ベイズの定理」とは、
事象Aが起こる確率をP(A)として、Aとは独立した事象Bが起こる確率をP(B)として場合、
事象Aが起きた後で、事象Bがおこる確率はP(B|A)であるが、P(B|A)にP(A)を掛け合わした確率P(B|A)*(A)(Aが起こる確率と、Aが起こったあとでBが起こる確率)は、その逆であるBが起こった後にAが起こる確率P(A|B)とBが起こる確率P(B)をかけ合わせたP(A|B)*P(B)と等しい。
P(B|A)*P(A) = P(A|B)*P(B)
この式を変形すればベイズの定理が得られる。
つまり、
P(B) = 事象 A が起きる前の、事象 B の確率(事前確率, prior probability)
P(B|A) = 事象 A が起きた後での、事象 B の確率(事後確率,条件付き確率, posterior probability,conditional probability)
とすると、ベイズの定理を使えば、事後確率 P(B|A) は上記に従って計算される。すなわち、事象Aに関するある結果(データ)が得られたとすると、それを反映し、事象Bが得られたあとのAが起こる確率P(A|B)の乗算によって、事象 B の確率は事前確率から事後確率へと更新される。
ここでは、 P(A|B) は尤度(likelihood)と呼ばれる。
なお事象 B の確率の観点からは、P(A) は規格化定数としての意味しかないため、しばしば省略される。つまり事後確率は事前確率と尤度の積に比例する。
————————————
ここで事象A=原因として、事象Bを結果とすると
P(B) = 原因が起きる前の、結果の確率(事前確率, prior probability)
P(B|A) = 原因が起きた後での、結果の確率(事後確率,条件付き確率, posterior probability,conditional probability)
P(結果|原因) ∝ P(原因|結果)*P(結果)
原因から結果が起こる確率は、
事後確率 = 尤度(原因|結果)*事前確率
となる。具体的には、統計モデルに当てはめて推定事前分布を決定し、調査によって得られた尤度(結果が解っているときの原因の確率)を求め、両者の積として、原因に基づく結果の確率を算定する。
————————————
頭痛が起こる確率P(A)、インフルエンザに罹患する確率P(B)が解っているとする。
インフルエンザに罹患して頭痛が発生している人を調査したところ、P(A|B)が得られた。
頭痛を訴えた人の中でインフルエンザに罹患している確率P(B|A)は、
P(インフルエンザ|頭痛) = P(頭痛|インフルエンザ) * P(インフルエンザ) / P(頭痛)
もしくは
P(インフルエンザ|頭痛) ∝ P(頭痛|インフルエンザ) * P(インフルエンザ)
となる。
————————————
ベイズ統計は、ベイズの定理を確率分布に拡張し、
事後確率分布 = 尤度*事前確率分布
————————————
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
第2章 共役事前分布
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
統計学では、調査・実験によって得られたデータを元に、その未知なる母集団の分布なり、真の分布を推定して、未来に起こりうることに対する予測を得たいわけである。適切な予測をえるためには、無茶苦茶な分布ではなくて、なんらかのモデルにはまるような分布であってほしい。とくに数学的にハマる分布であれば、調査・実験結果を用いて、算術的に未来に対する予測を立てることが可能となる。
ベイズ定理により、事前分布を推定し、調査・実験によって得られた尤度をかけ合わせれば推定事後分布が得られる。性質がよく解っている事前分布を用いれば、「共役事前分布」を用いることで、複雑な計算を回避して簡便に推定事後分布が得られる。ここで、共役事前分布は、尤度をかけて事後分布を求めると、その関数形が同じになるような事前分布のことである。共役事前分布を使えば、事前分布と事後分布は同じ形になる。
性質がよく解っている事前分布と尤度、事後分布の関係は以下のようになっている。
共役事前分布 ? ? ?母数が規定する確率分布 ? ?事後分布
ベータ分布 ? ? ? ? ベルヌーイ分布 ? ?ベータ分布
ベータ分布 ? ? ? ? 二項分布 ベータ分布
正規分布 ? ? 正規分布(σ2既知) ? ? ? ? ?正規分布
逆ガンマ分布 ? ? 正規分布(σ2未知) ? ? ? ? ? 逆ガンマ分布
ガンマ分布 ? ? ? ?ポアソン分布 ? ? ? ? ? ? ? ? ? ? ? ガンマ分布
ディリクレ分布 ? 多項分布 ? ? ? ? ? ? ? ? ? ? ? ? ? ?ディリクレ分布
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
このように共益事前分布を上手に利用して、調査・実験データから尤度を算定し、事前分布を推定して、ベイズの定理から事後分布を簡便に求めることができる。一方で、実際の統計データでは、常にこのような標準的な数学的分布にフィットする単純なモデルで描けるとは限らない。そこで、以下に示される一般線形モデルや、個体差を考慮した階層ベイズモデル(線形混合モデル)、さらに空間相関を考慮したCarモデルなどが有用となる。その場合、事後分布を推定する方法として、マルコフ・モンテカルロ法(MCMC法)が強力なツールとなる。
また、ベイズモデリングについて、BUGS言語を用いて策定し、BUGS言語に従ってベイズ解析を実行するWinBUGSをR言語ラッパー(R2WBwrapper.R)から操作する方法が利用できる。
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
第3章 ベイズモデル化一般線形モデル GLM:Generalized linear model
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
発生頻度がまれなる事象、例えば手術死亡率のようなものでれば、事前分布にポアソン分布を用いることが適当かもしれない。ポアソン分布の特徴は、平均値λが、分散σに等しい点である。
ここで、e はネイピア数 (e = 2.71828?)であり、k! は k の階乗を表す。
また、λ は所与の区間内で発生する事象の期待発生回数に等しい。
P(X = k) は、「所与の時間中に平均で λ 回発生する事象がちょうど k 回(k は非負の整数)発生する確率」に相当する。
発症数 yi は平均 λi のポアソン分布にしたがうとすると、
p(yi|λi)= λyi exp(−λi) / yi
i の平均 λi を以下のようにおいてみたら……
λi = exp(β1 + β2xi)
対数リンク関数
log(平均) = 線形予測子
線形予測子
β1は切片、β2は傾きとなる。
ポアソン分布は、平均(=分散)λで決定されるが、log(λi) = β1 + β2xiと規程したことで、
β1とβ2がポアソン分布を規定するパラメータとなる。
L(β1, β2) = Πp(yi|λi) = Πp(yi|β1,β2,xi)
X={xi}として、この尤度関数は、iで規程される離散確率分布なので、パラメーター{β1,β2}がある値を取っている時に
Yが得られる確率はp(Y|β1, β2) =L(β1, β2)
ベイズモデルでの事後分布は、(尤度)x(事前分布)に比例するので、
p(β1, β2|Y) ∝?p(Y|β1,β2)p(β1)p(β2)
つまりp(β1, β2|Y)は、事後分布であり、データYが与えられたときのパラメーター{β1,β2}の同時確率である。
p(β1)とp(β2)は、それぞれ切片β1と傾きβ2の事前分布であり、これら事前分布を適切に指定すればベイズモデル化した一般線形モデルGLMとなる。
尤度は確率 (あるいは確率密度) の積であり,大量のかけ算となり、計算が大変なので、パラメーターの最尤推定では,対数尤度関数 (log likelihood function) を使う。対数尤度 log L(λ) の最大化は尤度 L(λ) の最大化になる。
ここで、パラメータβ1、β2の事前分布をどうするかである。事前に情報がない場合、ベイズ流では、無情報事前分布を選択する。ここでは、βの無情報事前分布として、平べったい正規分布N(0,100)を選ぶ。
|
1 |
> curve(dnorm(x, 0, 1.0E-4), -1, 1, lwd = 3) |
dnorm(mean, tau) meanは平均、tauは分散の逆数, 標準偏差1/√tau
tau = 1/σ2=1.0E-4, σ^2 = 1000, σ= 100
サンプルデータをloadして、まずどんなデータか描画する。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
> load("d.RData") > d x y 1 3.000000 5 2 3.210526 3 3 3.421053 6 4 3.631579 7 5 3.842105 7 6 4.052632 5 7 4.263158 9 8 4.473684 9 9 4.684211 7 10 4.894737 10 11 5.105263 12 12 5.315789 8 13 5.526316 7 14 5.736842 4 15 5.947368 4 16 6.157895 11 17 6.368421 9 18 6.578947 9 19 6.789474 8 20 7.000000 6 |
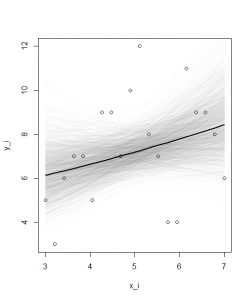
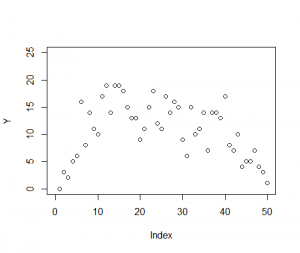
xが体サイズで、yが種子数。観測データを図にしてみる。
|
1 |
> plot(d$x, d$y) |
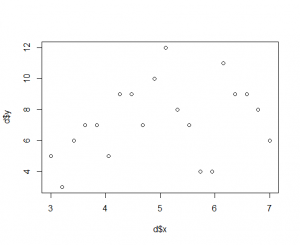
サイズがxi=5の場合、種子数yiが10-12個がプロットされている。xi=5がピークのように見えるが、全体としてはばらついているように見える。
BUGSコードを用いて、このモデルを記述する:BUGSモデル:ポアソン分布
|
1 2 3 4 5 6 7 8 9 10 |
model { Tau.noninformative <- 1.0E-4 for (i in 1:N) { Y[i] ~ dpois(lambda[i]) log(lambda[i]) <- beta1 + beta2 * (X[i] - Mean.X) } beta1 ~ dnorm(0, Tau.noninformative) beta2 ~ dnorm(0, Tau.noninformative) } |
次にBUGSの初期条件をRから入力していく。この際に、RからWinBUGSを操作するために「R2WBwrapper.R」を用いる。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
> source("R2WBwrapper.R") # reading "R2WBwrapper.R" (written by kubo@ees.hokudai.ac.jp)... 要求されたパッケージ coda をロード中です 要求されたパッケージ boot をロード中です > load("d.RData") > > clear.data.param() > set.data("N", nrow(d)) > set.data("Y", d$y) > set.data("X", d$x) > set.data("Mean.X", mean(d$x)) > > set.param("beta1", 0) > set.param("beta2", 0) > #WinBUGSを呼び出し、サンプリング結果をpost.bugsに格納 > post.bugs <- call.bugs( + file = "model.bug.txt", + n.iter = 1600, n.burnin = 100, n.thin = 3 + ) > post.mcmc <- to.mcmc(post.bugs) |
分析結果は、post.bugsに収まる。
R2WBwrapper.Rファイルで定義されているto.list()関数とto.mcmc()関数を用いて、post.bugsオブジェクトをそれぞれto.listクラスとmcmcクラスのオブジェクトに変換する。
|
1 2 3 4 5 6 |
> post.list <- to.list(post.bugs) > post.mcmc <- to.mcmc(post.bugs) > s<-colnames(post.mcmc) %in% c("beta1", "beta2") > s [1] TRUE TRUE FALSE > plot(post.list[,s,]) |
パラメータβ1とβ2の推定事後分布が以下のように得られた。
|
1 |
> plot(post.list[,"beta1",]) |
|
1 |
>plot(post.list[,"beta2",]) |
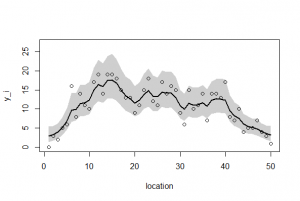
最後に、得られたパラメータβ1とβ2の推定事後分布を組み込んで、xiとyiの関係とλの事後分布のグラフを描く。
パラメータの事後分布からのサンプル
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
> post.mcmc <- as.mcmc(post.bugs$sims.matrix) > beta1 <- post.mcmc[, "beta1"] > beta2 <- post.mcmc[, "beta2"] > points(d$x, d$y) > add.mean(median(beta1), median(beta2), lty = 1, lwd = 2) > > par(ask = TRUE) > plot(d$x, d$y, type = "n", xlab = "x_i", ylab = "y_i") > for (i in 1:nrow(post.mcmc)) { + add.mean(beta1[i], beta2[i], lty = 1, col = "#00000004") + } > points(d$x, d$y) > add.mean(median(beta1), median(beta2), lty = 1, lwd = 2) |
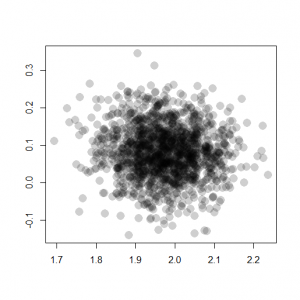
パラメータβ1とβ2の関係も散布図に描く。
|
1 2 3 4 5 6 |
> plot( + as.matrix(post.mcmc)[,c("beta1", "beta2")], + lty = 1, col = "#00000030", + pch = 16, cex = 2, + xlab = "", ylab = "" + ) |
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
R2WBWrapperを用いて、BUGS言語で記載した統計モデルのパラメータに初期値を与えていく。
得られたデータを元に、作図のRコードでグラフ表示する。
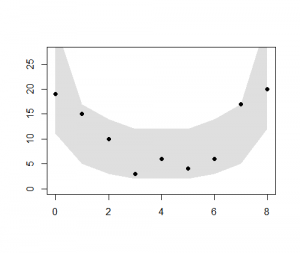
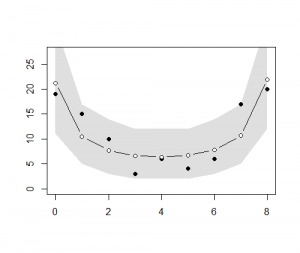
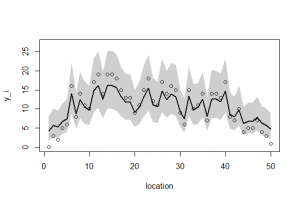
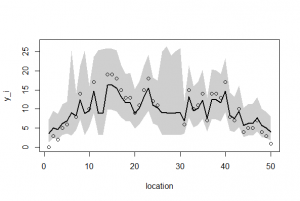
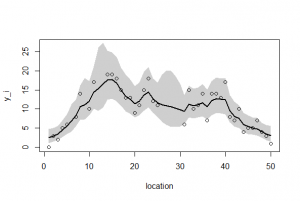
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー 空間的な両端を除いて、 p(rj|μj,s) のばらつきのパラメータsはその場所でも同じと仮定する。このような事前分布は条件付き自己回帰(conditional auto regressive, CAR)モデルと呼ばれる。ここのでモデルのようにさまざまな制約をつけて簡単にしたものはintrinsic Gaussian CARモデルと分類される。 BUGSコードでの注意点は、 car.normal()関数は、intrinsic Gaussian CARモデルから[rj}のMCMCサンプルを発生させる関数である。Adj[]は隣接する場所の番号j、 グラフを描画させる。 ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー 全部まとめて推定 (欠測あり・なし,CAR と GLMM) post.bugsには、4種類(欠損なしGLMM、欠損ありGLMM、欠損なしCarモデル、欠損ありCarモデル)の分析結果βとr[i]が含まれている。 欠損データあるなし、およびGLMMもしくはCarモデルの通りを上記BUGSモデルと、欠損データを作成するRを読み込んで、以下のように実行する。 ここでは、 2.欠損あり、GLMMモデル このように、Carモデルが欠損データを上手に取り扱えることが示された。
第4章 階層ベイズ化された一般線形混合モデル(個体差の有る場合) GLMM:Generalized linear mixed model
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
次に、基本「有る無し」データのような二項分布に従うモデルで、個体差riを伴なう場合のモデル化を行う。
リンク関数と線形予測子を
logit(qi) = β + ri
とする。
切片β, 個体差riは、平均ゼロ標準偏差sの正規分布に従う。
p(ri|s)を階層事前分布と呼ぶ。「階層」とは、事前分布のパラメータにさらに事前分布が設定されていることをいう。また階層事前分布のパラメータsは超パラメータ(hyper parameter)、p(s)は超事前分布と呼ぶ。このような階層事前分布を使っているベイズ統計モデルが階層ベイズ統計モデルである。
ここでβには、無情報事前分布として平坦な正規分布N(0,100)を用いるとして、個体差riの階層事前分布には平均値ゼロで標準偏差がsの正規分布、この階層事前分布のばらつきsの事前分布は0
第5章 空間構造のある階層ベイズモデル
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
平均値λjを線形予測子と対数リンク関数を用いて、
logλj = β + ri
とする。
ここで空間の中で近傍のデータが影響するとする。
例えば、近傍とは空間的位置関係で隣の位置するものだけとし、その影響は均質に1/njだと規程する。
すると、ここでは近傍rj-1とrj+1の平均μiとし、μiが影響するとすれば、
rjの代わりにrj-μjを用いる正規分布
μi = (rj-1+rj+1)/k2
端の部分は、μ1=r2, μi=ri-1
r[1:N.site]~car.normal(Adj[], Weights[], Num[], tau)
Weights[]はAdj[]に対応する重み、
Num[]はそれぞれの区画に隣接する場所の数nj、
tauは分散の逆数、つまり1/s^2。
第6章 空間相関モデルと欠測のある観測データ
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
空間相関のモデルであるCarモデルは、GLMMモデルと比較して、観測データに欠損のあるデータ分析を適切にハンドリングできる。以下、欠損有るなし、GLMMかCarモデルかの4通りをまとめて推定して比較するBUGSモデルを作成する。
Yに対して欠損データYnoを作成するためのコードを以下に示す。
http://hosho.ees.hokudai.ac.jp/~kubo/stat/iwanamibook/fig/spatial/set.data.R
http://hosho.ees.hokudai.ac.jp/~kubo/stat/iwanamibook/fig/spatial/runbugs.R
post.bugs <- call.bugs(n.iter = 10100, n.burnin = 100, n.thin = 10)
で指定されているように、10100回のサンプリング、burn-inの100回、10個ごとの間引きで、1ループで1000個のデータが生成される。デフォルトで3ループ繰り返されるので、3000データが生成されて、post.listには1000個づつx3ループ、post.mcmcには3000行のデータxパラメータ数列となる。
post.mcmcのr[i]のデータからquantile()関数を用いて、mre[1]に中位点、mre[2]に2.5%位点、mre[3]に97.5%位点を求めている。
今回の分析では、4つの異なる条件(欠損データあるなし、GLMMかCarモデルか)がまとめてpost.bugsに収められており、個体差のデータr[i]も二次元r[j,i]となっているために"r[%i]"を"r[j,%i]とする。また欠損なしのデータYに対して、欠損ありデータYnoを指定し、またパラメータbetaには、beta[1]?beta[4]を指定する。
1. 欠損なし、GLMMモデル



![{\displaystyle {\begin{aligned}\mathrm {E} [X]&=\lambda ,\\\mathrm {V} [X]&=\lambda .\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f28bc6f94b1fc1b5fdae220742ee7471c5ed4de2)