ベイズモデル化について、理解できた部分と、依然、全体的には「もやー」とした状態。もう少し、丁寧に分析してみよう。
ーーーーーーーーーーーーーーーーーーーーーーーーーー
データ解析のための統計モデリング入門:第9章「GLMのベイズモデル化と事後分布の確定」について、より詳細に分析してみる。
ーーーーーーーーーーーーーーーーーーーーーーーーーー
9.1 例題:趣旨数のポアソン回帰(個体差なし)
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
> load("d.RData") > d x y 1 3.000000 5 2 3.210526 3 3 3.421053 6 4 3.631579 7 5 3.842105 7 6 4.052632 5 7 4.263158 9 8 4.473684 9 9 4.684211 7 10 4.894737 10 11 5.105263 12 12 5.315789 8 13 5.526316 7 14 5.736842 4 15 5.947368 4 16 6.157895 11 17 6.368421 9 18 6.578947 9 19 6.789474 8 20 7.000000 6 |
xが体サイズで、yが種子数。観測データを図にしてみる。
|
1 |
> plot(d$x, d$y) |
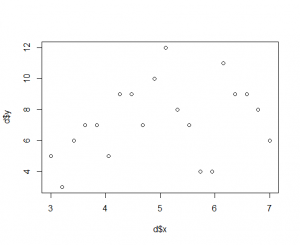
サイズがxi=5の場合、種子数yiが10-12個がプロットされている。xi=5がピークのように見えるが、全体としてはばらついているように見える。
クラス関数class()で、変数dのクラスを調べるとdata.frameクラスが返る。
|
1 2 |
> class(d) [1] "data.frame" |
lenght()関数をdに当てはめると、2と返す。要するにxとyとで2ということか。
|
1 2 |
> length(d) [1] 2 |
summary()関数でdの標本平均や最小値、最大値、四分位数を返す。
|
1 2 3 4 5 6 7 8 |
> summary(d) x y Min. :3 Min. : 3.00 1st Qu.:4 1st Qu.: 5.75 Median :5 Median : 7.00 Mean :5 Mean : 7.30 3rd Qu.:6 3rd Qu.: 9.00 Max. :7 Max. :12.00 |
体サイズxの最小値は3で最大値は7、平均値が5、メディアンが5
種子数yの最小値は3.00、最大値は12.00、平均値は7.30、メディアン7.00
度数分布を得るためtable()関数で調べてみると、
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 |
> table(d) y x 3 4 5 6 7 8 9 10 11 12 3 0 0 1 0 0 0 0 0 0 0 3.21052631578947 1 0 0 0 0 0 0 0 0 0 3.42105263157895 0 0 0 1 0 0 0 0 0 0 3.63157894736842 0 0 0 0 1 0 0 0 0 0 3.84210526315789 0 0 0 0 1 0 0 0 0 0 4.05263157894737 0 0 1 0 0 0 0 0 0 0 4.26315789473684 0 0 0 0 0 0 1 0 0 0 4.47368421052632 0 0 0 0 0 0 1 0 0 0 4.68421052631579 0 0 0 0 1 0 0 0 0 0 4.89473684210526 0 0 0 0 0 0 0 1 0 0 5.10526315789474 0 0 0 0 0 0 0 0 0 1 5.31578947368421 0 0 0 0 0 1 0 0 0 0 5.52631578947368 0 0 0 0 1 0 0 0 0 0 5.73684210526316 0 1 0 0 0 0 0 0 0 0 5.94736842105263 0 1 0 0 0 0 0 0 0 0 6.15789473684211 0 0 0 0 0 0 0 0 1 0 6.36842105263158 0 0 0 0 0 0 1 0 0 0 6.57894736842105 0 0 0 0 0 0 1 0 0 0 6.78947368421053 0 0 0 0 0 1 0 0 0 0 7 0 0 0 1 0 0 0 0 0 0 > table(d$x) 3 3.21052631578947 3.42105263157895 3.63157894736842 1 1 1 1 3.84210526315789 4.05263157894737 4.26315789473684 4.47368421052632 1 1 1 1 4.68421052631579 4.89473684210526 5.10526315789474 5.31578947368421 1 1 1 1 5.52631578947368 5.73684210526316 5.94736842105263 6.15789473684211 1 1 1 1 6.36842105263158 6.57894736842105 6.78947368421053 7 1 1 1 1 > table(d$y) 3 4 5 6 7 8 9 10 11 12 1 2 2 2 4 2 4 1 1 1 |
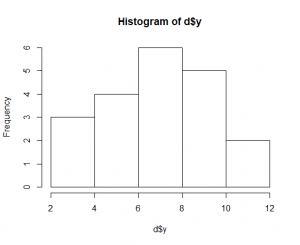
種子数のヒストグラムを出すと、
|
1 |
> hist(d$y) |
xとyの分散を調べておく
|
1 2 3 4 |
> var(d$x) [1] 1.551247 > var(d$y) [1] 5.8 |
xとyの標準偏差
|
1 2 3 4 |
> sd(d$x) [1] 1.24549 > sd(d$y) [1] 2.408319 |
ポアソン回帰の統計モデルとして、平均λiを説明変数xiの関数として、ある個体iの平均種子数λiは
、
線形予測子>
λi = exp(β1 + β2xi)
β2は傾き、β1は切片
対数リンク関数>
logλi = β1 + β2xi
ポアソン回帰でβの最尤推定値を求めると、
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
> fit <- glm(y~x, data = d, family = poisson) > fit Call: glm(formula = y ~ x, family = poisson, data = d) Coefficients: (Intercept) x 1.56606 0.08334 Degrees of Freedom: 19 Total (i.e. Null); 18 Residual Null Deviance: 15.66 Residual Deviance: 14.17 AIC: 94.04 β1=1.57、β2=0.0083 |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
> summary(fit) Call: glm(formula = y ~ x, family = poisson, data = d) Deviance Residuals: Min 1Q Median 3Q Max -1.52168 -0.53195 0.06417 0.40797 1.57939 Coefficients: Estimate Std. Error z value Pr(>|z|) (Intercept) 1.56606 0.35995 4.351 1.36e-05 *** x 0.08334 0.06838 1.219 0.223 --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 (Dispersion parameter for poisson family taken to be 1) Null deviance: 15.660 on 19 degrees of freedom Residual deviance: 14.171 on 18 degrees of freedom AIC: 94.036 Number of Fisher Scoring iterations: 4 |
|
1 2 |
> xx <- seq(min(d$x), max(d$x), length =100) > lines(xx, exp(1.57 + 0.083 *xx), lwd = 2) |
9.4 ベイズ統計モデルの事後分布の推定
9.4.1 ベイズ統計モデルのコーディング
βの事前分布=平べったい正規分布N(0,100)
|
1 |
> curve(dnorm(x, 0, 1.0E-4), -1, 1, lwd = 3) |
dnorm(mean, tau) meanは平均、tauは分散の逆数, 標準偏差1/√tau
tau = 1/σ2=1.0E-4, σ^2 = 1000, σ= 100
BUGSモデル:ポアソン分布
|
1 2 3 4 5 6 7 8 9 10 |
model { Tau.noninformative <- 1.0E-4 for (i in 1:N) { Y[i] ~ dpois(lambda[i]) log(lambda[i]) <- beta1 + beta2 * (X[i] - Mean.X) } beta1 ~ dnorm(0, Tau.noninformative) beta2 ~ dnorm(0, Tau.noninformative) } |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
> source("R2WBwrapper.R") # reading "R2WBwrapper.R" (written by kubo@ees.hokudai.ac.jp)... 要求されたパッケージ coda をロード中です 要求されたパッケージ boot をロード中です > load("d.RData") > > clear.data.param() > set.data("N", nrow(d)) > set.data("Y", d$y) > set.data("X", d$x) > set.data("Mean.X", mean(d$x)) > > set.param("beta1", 0) > set.param("beta2", 0) > #WinBUGSを呼び出し、サンプリング結果をpost.bugsに格納 > post.bugs <- call.bugs( + file = "model.bug.txt", + n.iter = 1600, n.burnin = 100, n.thin = 3 + ) > post.mcmc <- to.mcmc(post.bugs) |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
> post.bugs Inference for Bugs model at "C:/Users/teiji/Desktop/Stat/stat/model.bug.txt", fit using WinBUGS, 3 chains, each with 1600 iterations (first 100 discarded), n.thin = 3 n.sims = 1500 iterations saved mean sd 2.5% 25% 50% 75% 97.5% Rhat n.eff beta1 2.0 0.1 1.8 1.9 2.0 2.0 2.1 1 1100 beta2 0.1 0.1 -0.1 0.0 0.1 0.1 0.2 1 610 deviance 92.0 2.0 90.1 90.6 91.4 92.9 97.3 1 1500 For each parameter, n.eff is a crude measure of effective sample size, and Rhat is the potential scale reduction factor (at convergence, Rhat=1). DIC info (using the rule, pD = Dbar-Dhat) pD = 2.0 and DIC = 94.0 DIC is an estimate of expected predictive error (lower deviance is better). |
R2WBwrapper.Rファイルで定義されているto.list()関数とto.mcmc()関数を用いて、post.bugsオブジェクトをそれぞれto.listクラスとmcmcクラスのオブジェクトに変換する。
|
1 2 3 4 5 6 |
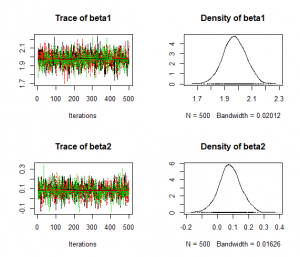
> post.list <- to.list(post.bugs) > post.mcmc <- to.mcmc(post.bugs) > s<-colnames(post.mcmc) %in% c("beta1", "beta2") > s [1] TRUE TRUE FALSE > plot(post.list[,s,]) |
|
1 2 3 4 5 6 7 8 |
to.list <- function(x.bugs) mcmc.list( lapply( 1:x.bugs$n.chain, function(chain) as.mcmc(x.bugs$sims.array[, chain,]) ) ) to.mcmc <- function(x.bugs) as.mcmc(x.bugs$sims.matrix) |
|
1 2 |
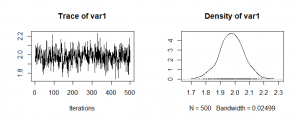
> plot(post.list[,s,]) > plot(post.bugs) |
|
1 |
> plot(post.list[,"beta1",]) |
|
1 |
>plot(post.list[,"beta2",]) |
post.bugs以後の処理
post.bugsのクラスを調べると
|
1 2 |
> class(post.bugs) [1] "bugs" |
bugsと返される。
R2WBrapper.Rの中に記載されているように、
|
1 2 3 4 5 6 7 8 9 |
# Post processings ======================================================= to.list <- function(x.bugs) mcmc.list( lapply( 1:x.bugs$n.chain, function(chain) as.mcmc(x.bugs$sims.array[, chain,]) ) ) to.mcmc <- function(x.bugs) as.mcmc(x.bugs$sims.matrix) |
post.listの中身には、3回回したMCMCのデータが入っている。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 |
[[1]] Markov Chain Monte Carlo (MCMC) output: Start = 1 End = 500 Thinning interval = 1 beta1 beta2 deviance [1,] 1.921 2.031e-02 91.52 [2,] 1.981 8.260e-02 90.04 [3,] 1.924 5.892e-02 90.70 [4,] 2.105 9.572e-02 92.41 [5,] 2.030 4.514e-02 90.63 ...... [333,] 2.057 0.1415000 91.81 [ reached getOption("max.print") -- omitted 167 rows ] [[2]] Markov Chain Monte Carlo (MCMC) output: Start = 1 End = 500 Thinning interval = 1 beta1 beta2 deviance [1,] 2.032 0.1039000 90.53 [2,] 2.075 0.1365000 92.16 [3,] 2.006 0.0758300 90.12 [4,] 1.935 0.0852500 90.36 [5,] 2.001 -0.0044740 91.72 ...... [333,] 2.057 0.1415000 91.81 [ reached getOption("max.print") -- omitted 167 rows ] [[3]] Markov Chain Monte Carlo (MCMC) output: Start = 1 End = 500 Thinning interval = 1 beta1 beta2 deviance [1,] 1.920 0.0135800 91.74 [2,] 1.759 0.2276000 99.43 [3,] 1.910 -0.0031110 92.50 [4,] 1.903 0.0714400 91.00 [5,] 1.906 0.0553600 91.10 ...... [333,] 1.857 0.0606800 92.44 [ reached getOption("max.print") -- omitted 167 rows ] attr(,"class") [1] "mcmc.list" |
post.mcmcには、どうやら生のmcmcデータ 500×3=1500 含まれているようだ。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
> post.mcmc Markov Chain Monte Carlo (MCMC) output: Start = 1 End = 1500 Thinning interval = 1 beta1 beta2 deviance [1,] 2.016 1.062e-01 90.35 [2,] 1.822 1.408e-01 93.93 [3,] 2.002 2.260e-02 90.86 [4,] 1.881 2.320e-01 95.36 [5,] 2.064 9.390e-02 91.07 ....... [333,] 1.919 1.045e-01 90.65 [ reached getOption("max.print") -- omitted 1167 rows ] |
1ループ目のMCMC結果だけ取り出してpost.list_1に挿入する。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
> post.list_1 <- post.list[[1]] > post.list_1 Markov Chain Monte Carlo (MCMC) output: Start = 1 End = 500 Thinning interval = 1 beta1 beta2 deviance [1,] 1.921 2.031e-02 91.52 [2,] 1.981 8.260e-02 90.04 [3,] 1.924 5.892e-02 90.70 [4,] 2.105 9.572e-02 92.41 [5,] 2.030 4.514e-02 90.63 ...... [330,] 1.907 4.293e-02 91.28 [331,] 1.926 2.969e-02 91.19 [332,] 1.983 2.380e-02 90.80 [333,] 2.147 1.635e-01 96.37 [ reached getOption("max.print") -- omitted 167 rows ] |
さらに1ループ目のパラメータβ1だけをpost.list_1[,1]で覗いてみる。500個のデータが含まれている。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
> length(post.list_1[,1]) [1] 500 > post.list_1[,1] Markov Chain Monte Carlo (MCMC) output: Start = 1 End = 500 Thinning interval = 1 [1] 1.921 1.981 1.924 2.105 2.030 1.969 2.079 1.888 [9] 2.018 1.967 2.049 2.124 2.048 1.984 1.905 1.985 [17] 2.076 1.938 1.936 1.989 1.996 2.012 2.092 2.023 [25] 1.949 2.109 2.017 1.906 1.922 1.983 1.909 1.912 ....... [489] 1.968 1.979 1.780 1.983 1.789 2.044 2.184 1.906 [497] 1.937 2.096 2.008 1.920 > plot(post.list_1[,1]) |
post.mcmcについても、1列目のβ1だけをのぞいてみると、1500個のデータ
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
> length(post.mcmc[,1]) [1] 1500 > post.mcmc[,1] Markov Chain Monte Carlo (MCMC) output: Start = 1 End = 1500 Thinning interval = 1 [1] 2.016 1.822 2.002 1.881 2.064 2.086 1.904 1.969 [9] 2.036 1.938 1.959 2.114 2.062 1.921 2.026 1.995 ...... [993] 2.085 1.949 2.008 1.810 2.043 1.911 1.843 1.806 [ reached getOption("max.print") -- omitted 500 entries ] > plot(post.mcmc[,1]) |
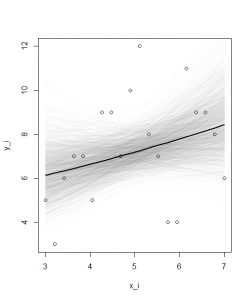
パラメータの事後分布からのサンプル
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
> post.mcmc <- as.mcmc(post.bugs$sims.matrix) > beta1 <- post.mcmc[, "beta1"] > beta2 <- post.mcmc[, "beta2"] > points(d$x, d$y) > add.mean(median(beta1), median(beta2), lty = 1, lwd = 2) > > par(ask = TRUE) > plot(d$x, d$y, type = "n", xlab = "x_i", ylab = "y_i") > for (i in 1:nrow(post.mcmc)) { + add.mean(beta1[i], beta2[i], lty = 1, col = "#00000004") + } > points(d$x, d$y) > add.mean(median(beta1), median(beta2), lty = 1, lwd = 2) |
|
1 2 3 4 5 6 |
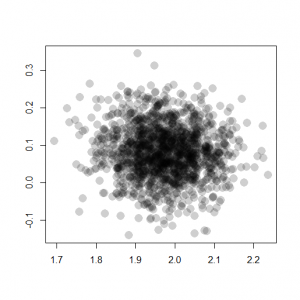
> plot( + as.matrix(post.mcmc)[,c("beta1", "beta2")], + lty = 1, col = "#00000030", + pch = 16, cex = 2, + xlab = "", ylab = "" + ) |
9.5.1 事後分布の統計量
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
> print(post.bugs, digits.summary = 3) Inference for Bugs model at "C:/Users/teiji/Desktop/Stat/stat/model.bug.txt", fit using WinBUGS, 3 chains, each with 1600 iterations (first 100 discarded), n.thin = 3 n.sims = 1500 iterations saved mean sd 2.5% 25% 50% 75% 97.5% Rhat n.eff beta1 1.974 0.082 1.812 1.919 1.973 2.031 2.132 1.002 1100 beta2 0.081 0.069 -0.058 0.037 0.079 0.126 0.221 1.003 610 deviance 92.035 2.004 90.095 90.580 91.395 92.872 97.290 1.002 1500 For each parameter, n.eff is a crude measure of effective sample size, and Rhat is the potential scale reduction factor (at convergence, Rhat=1). DIC info (using the rule, pD = Dbar-Dhat) pD = 2.0 and DIC = 94.0 DIC is an estimate of expected predictive error (lower deviance is better). |