7.5 交換可能性を事前の確信とするモデリング
事前分布として、真の死亡率λ1,…,λ94はガンマ分布gamma(α, α/μ)からのランダムな標本だと仮定する。
g(λ|α,μ) λの事前平均と分散は、それぞれμとμ^2/αで与えられる。

μには、逆ガンマ分布inverse gamma(a,b)、αには密度g(α)を割り当てる。

２つの病院の死亡率λ1とλ2の事前分布を取り上げる
g(λ1,λ2|α0)は、μを積分消去することが可能となり、算出できる。

対数事前密度を計算するpgexchprior()関数：引数は真の死亡率ベクトルlambdaと事前分布のパラメータα0, a, bからなるベクトルpars

> pgexchprior=function(lambda,pars)
+ {
+ alpha=pars[1]; a=pars[2]; b=pars[3]
+ (alpha-1)*log(prod(lambda))-(2*alpha+a)*log(alpha*sum(lambda)+b)
+ }

ここでμにパラメータa=10, b=10の逆ガンマ分布inverse gamma(10,10)を割り当てる。
次のコードでは、α0が5, 20, 80, 400に等しい場合の(λ1, λ2)の結合密度を投稿線図を作成する。

> alpha=c(5,20,80,400); par(mfrow=c(2,2))
> for (j in 1:4)
+ mycontour(pgexchprior,c(.001,5,.001,5),c(alpha[j],10,10),
+ main=paste(“ALPHA = “,alpha[j]),xlab=”LAMBDA 1″,ylab=”LAMBDA 2”)

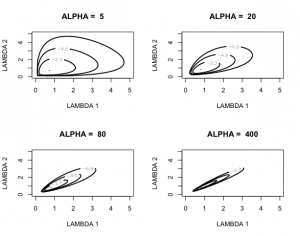
逆ガンマ分布inverse gamma(10,10)が割り当てられているので、真の死亡率λ1とλ2はどちらも１を中心とする。超パラメータαは、精度パラメータである。α=400と固定すると、λ1=λ2の直線沿いに集中する。

7.6 事後分布
λiの事後分布はガンマ分布gamma(yi+α, ei+α/μ)にしたがう。
λiの事後平均はαとμを条件として、E(λi|y,α,μ)で表される。

p(α,μ|data)

7.7 事後分布からのシミュレーション

g(超パラメータ|data)g(真の率|超パラメータ, data)
次のようにして事後結合密度からランダム標本をシミュレーションできる。
　周辺事後分布から(μ, α）をシミュレーションする。
　シミュレーションされたμとαの値を条件としてλ1,….,λ94

θ1 = log(α）、θ2 = log(μ)
変換されたパラメータの周辺事後密度p(θ1,θ2|data)

poissgamexch()関数にはθ1, θ2の対数事後分布の定義が含まれる。

poissgamexch=function (theta, datapar)
{
y = datapar$data[, 2]
e = datapar$data[, 1]
z0 = datapar$z0
alpha = exp(theta[1])
mu = exp(theta[2])
beta = alpha/mu

logf=function(y,e,alpha,beta)
lgamma(alpha + y) – (y + alpha) * log(e + beta) +
alpha * log(beta)-lgamma(alpha)

val=sum(logf(y,e,alpha,beta))
val = val + log(alpha) – 2 * log(alpha + z0)
return(val)
}

laplace()関数で事後モードと分散共分散行列を求める。
初期値として(θ1,θ2) = (2, -7)を使ったネルダー・ミード法アルゴリズムを実行。

> datapar = list(data = hearttransplants, z0 = 0.53)
> start=c(2, -7)
> fit = laplace(poissgamexch, start, datapar)
> fit
$mode
[1] 1.883954 -6.955446

$var
[,1] [,2]
[1,] 0.233694921 -0.003086655
[2,] -0.003086655 0.005866020

$int
[1] -2208.503

$converge
[1] TRUE

> par(mfrow = c(1, 1))
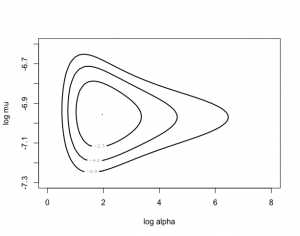
> mycontour(poissgamexch, c(0, 8, -7.3, -6.6), datapar,
+ xlab=”log alpha”,ylab=”log mu”)

(θ1,θ2)の事後密度は正規形ではない。θ1=log α
gibbs()関数のギブス内メトロポリスアルゴリズムを使って、（θ1,θ2）= (4, -7)からはじめ、
メトロポリス法で尺度パラメータc1=1, c2=0.15として1000サイクル繰り返しを行っている。

> start = c(4, -7)
> fitgibbs = gibbs(poissgamexch, start, 1000, c(1,.15), datapar)
> fitgibbs$accept
[,1] [,2]
[1,] 0.506 0.51

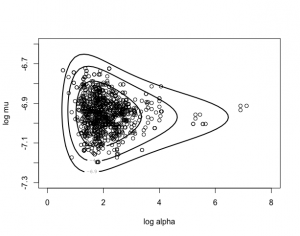
> mycontour(poissgamexch, c(0, 8, -7.3, -6.6), datapar,
+ xlab=”log alpha”,ylab=”log mu”)
> points(fitgibbs$par[, 1], fitgibbs$par[, 2])

精度パラメータθ1=log αの周辺密度からシミュレーションした標本のカーネル密度推定値

> plot(density(fitgibbs$par[, 1], bw = 0.2))

事後分布からシミュレーションした値を使って、真の死亡率λiを検討する。
超パラメータαとμの値が与えられると、真の死亡率はλiがガンマ分布gamma(y1+α,ei+α/μ)である独立した事後分布に従う。それぞれの死亡率について、rgamma()関数を使って、ガンマ関数から標本を抽出。
> alpha = exp(fitgibbs$par[, 1])
> mu = exp(fitgibbs$par[, 2])
> lam1 = rgamma(1000, y[1] + alpha, e[1] + alpha/mu)

それぞれの死亡率λ1について、1000個のシミュレーションをし、5%-95%の分位点を計算することで標本を要約する。

7.8 事後推論
真の死亡率{λi}と超パラメータμとαをシミュレーションした標本が結合事後分布から生成ー＞この標本をさまざまな推論に利用する。

7.8.1 縮約
病院iの真の死亡率λiの事後平均は以下で近似可能。
E(λi|data)

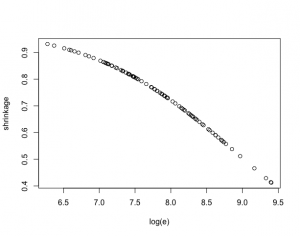
病院iでの観測死亡率yi/eiの縮約サイズ。
> shrink=function(i) mean(alpha/(alpha + e[i] * mu))
> shrinkage=sapply(1:94, shrink)
> plot(log(e), shrinkage)

7.8.2 病院間の比較

> mrate=function(i) mean(rgamma(1000, y[i] + alpha, e[i] + alpha/mu))
> hospital=1:94
> meanrate=sapply(hospital,mrate)
> hospital[meanrate==min(meanrate)]
[1] 93

> sim.lambda=function(i) rgamma(1000,y[i]+alpha,e[i]+alpha/mu)
> LAM=sapply(1:94,sim.lambda)
>
> compare.rates <- function(x) { + nc <- NCOL(x) + ij <- as.matrix(expand.grid(1:nc, 1:nc)) + m <- as.matrix(x[,ij[,1]] > x[,ij[,2]])
+ matrix(colMeans(m), nc, nc, byrow = TRUE)
+ }
> better=compare.rates(LAM)

> better[1:24,85]
[1] 0.029 0.034 0.044 0.043 0.038 0.044 0.041 0.057 0.039 0.052 0.035 0.067
[13] 0.041 0.038 0.046 0.037 0.044 0.066 0.189 0.045 0.034 0.043 0.047 0.054

7.9 ベイズ感度分析
一次元の推論で事前分布を変更する場合のSIRアルゴリズムを実装するsir.old.new()関数を作成する。
引数は、thetaはもとの事後密度からの標本であり, prior()はもとの事前密度を定義する関数で、prior.new()は新しい事後密度を定義する関数である。出力は新しい事後標本となっている。

> sir.old.new=function(theta, prior, prior.new)
+ {
+ log.g=log(prior(theta))
+ log.g.new=log(prior.new(theta))
+ wt=exp(log.g.new-log.g-max(log.g.new-log.g))
+ probs=wt/sum(wt)
+ n=length(probs)
+ indices=sample(1:n,size=n,prob=probs,replace=TRUE)
+ theta[indices]
+ }

> prior=function(theta)
+ 0.53*exp(theta)/(exp(theta)+0.53)^2
> prior.new=function(theta)
+ 5*exp(theta)/(exp(theta)+5)^2

> log.alpha=fitgibbs$par[, 1]
> log.alpha.new=sir.old.new(log.alpha, prior, prior.new)

7.10 事後予測モデルの検証
> lam94=rgamma(1000,y[94]+alpha,e[94]+alpha/mu)
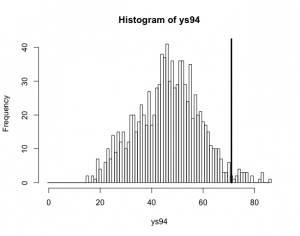
> ys94=rpois(1000,e[94]*lam94)

> hist(ys94,breaks=seq(-0.5,max(ys94)+0.5))
> lines(y[94]*c(1,1),c(0,100),lwd=3)

> prob.out=function(i)
+ {
+ lami=rgamma(1000,y[i]+alpha,e[i]+alpha/mu)
+ ysi=rpois(1000,e[i]*lami)
+ pleft=sum(ysi<=y[i])/1000 + pright=sum(ysi>=y[i])/1000
+ min(pleft,pright)
+ }
> pout.exchange=sapply(1:94,prob.out)
> plot(pout,pout.exchange,xlab=”P(extreme), equal means”,
+ ylab=”P(extreme), exchangeable”)
> abline(0,1)