Bayesian Comuputation with R
6.3 メトロポリス-ヘイスティング・アルゴリズム
<やっとたどり着いたMCMC法!>
事後密度g(θ|y)からシミュレーションを行う。
初期値θ0から数列θt-1の(t-1)番目の値が与えられている時、数列θtの値をシミュレーションするルールを定める。
候補の値θ*をシミュレーションする提案密度(proposal density)と、候補の値を数列の次の値として受け入れるかどうかを判断する受理確率(acceptance probability)Pの計算で構成される。
具体的には、
1. 提案密度p(θ*|θt-1)から候補の値θ*をシミュレーションする。
2. 次の比を計算する。R= g((θ*)p(θt-1|θ*) / g(θt-1)p(θ*|θt-1)
3. 受理確率 P=min{R, 1}を計算する。
4. θt=θ*となるような値θtを確率Pで満たせば標本とする。さもなければそのままθt=θt-1とする。
提案密度p(θ*|θt-1)が数列の現在の値と独立である場合、独立連鎖と定義する。
提案密度p(θ*|θt-1)=p(θ*)
この提案密度は次の形式で定義できる
提案密度p(θ*|θt-1) = h(θ* – θt-2)
このタイプのランダムウォーク連鎖では、比Rは
R=g(θ*)/g(θt-1)
rwnetrop()関数:ランダムウォーク連鎖
θ*= θt-1 + scale Z
Zは平均ベクトル0, 分散共分散行列Vの多変量正規分布で、scaleは正の尺度パラメータ.
indepmetrop()関数:独立連鎖
θ*の平均密度は平均ベクトルμ、分散共分散行列Vの多変量正規分布
メトロポリス-ヘイスティング・アルゴリズムを使うには、最初に提案密度を定めて、シミュレーション標本を上記関数で求める。
出力は、par:シミュレーション標本行列、accept:アルゴリズムの受理率
6.4 ギブスサンプリング
gibbs()関数
θi* = θit + ci*Z
Zは標準積分布に従う変量. ciは固定化された尺度パラメータ
θiの次のシミュレーションによる値θit+1は、P=min{1, g(θi*)/g(θit)}の確率で、次の候補と等しくなる。さもなければθit+1=θitとする。
gibbs()の引数は、対数事後密度を定義する関数、シミュレーションの初期値、ギブスのサイクル数、c,…cpを要素とする尺度パラメータ. 出力は、par:シミュレーション標本行列、accept:アルゴリズムの受理率
6.5 MCMC出力の分析
MCMCアルゴリズムでは、j回目の繰り返しでシミュレーションされる値の分布θjは、jが無限に近づくと事後分布からの抽出に「理論的には」収束する。しかしながら、シミュレーションした標本が事後密度g(θ|data)を十分に近似しているかどうかを結果から判断することはできない。
MCMC出力分析(MCMC output ana;ysis):受理率のチェック、グラフ作成、シミュレーション標本の統計量計算など
->連鎖が事後分布全体を十分に探索しているか、また抽出された数列が近似的に収束しているか。
MCMC出力の重要な点>バーンイン期間のサイズを見極めること。
ー>試行回数に対するθの要素、あるいはθの関数のシミュレーションされた値についてトレースプロットを調べる。トレースプロットは、特に事後分布の中心から離れたパラメータ値で初期化を行う場合には重要となる。
次に重要となる事項:標本値の自己相関の程度:連鎖で連続する値に強い相関があると、アルゴリズム全体が
パラメータ空間全体を探索する妨げとなる。
集合{θj}と{θj+L}の間の相関を計る自己相関である。Lはラグ:2つの集合の間の繰り返し数。
ラグの値に対する自己相関値のプロットを行う。連鎖が十分に混ざっておれば、ラグの増加に伴い、自己相関はゼロに近づく。
6.6 ベイズの計算での方策
マルコフ連鎖シミュレーションアルゴリズム
laplace()関数で事後密度を定める。
6.7 グループ化データから正規母集団を検討する
> d=list(int.lo=c(-Inf,seq(66,74,by=2)),
+ int.hi=c(seq(66,74,by=2), Inf),
+ f=c(14,30,49,70,33,15))
>
> y=c(rep(65,14),rep(67,30),rep(69,49),rep(71,70),rep(73,33),
+ rep(75,15))
> mean(y)
[1] 70.16588
>
> log(sd(y))
[1] 0.9504117
(μ, log σ)の事後分布は近似的に(70, 1)
> start=c(70,1)
> fit=laplace(groupeddatapost,start,d)
> fit
$mode
[1] 70.169880 0.973644
$var
[,1] [,2]
[1,] 3.534713e-02 3.520776e-05
[2,] 3.520776e-05 3.146470e-03
$int
[1] -350.6305
$converge
[1] TRUE
(μ, log σ)の事後モードは(70.17, 0.97)
パラメータの事後標準偏差は、分散共分散行列の対角成分の平方根を計算する。
> modal.sds=sqrt(diag(fit$var))
>
> proposal=list(var=fit$var,scale=2)
> fit2=rwmetrop(groupeddatapost,proposal,start,10000,d)
>
> fit2$accept
[1] 0.2941
>
> post.means=apply(fit2$par,2,mean)
> post.sds=apply(fit2$par,2,sd)
>
> cbind(c(fit$mode),modal.sds)
modal.sds
[1,] 70.169880 0.18800834
[2,] 0.973644 0.05609341
>
> cbind(post.means,post.sds)
post.means post.sds
[1,] 70.1705911 0.18782826
[2,] 0.9803252 0.05605967
>
> mycontour(groupeddatapost,c(69,71,.6,1.3),d,
+ xlab=”mu”,ylab=”log sigma”)
> points(fit2$par[5001:10000,1],fit2$par[5001:10000,2])
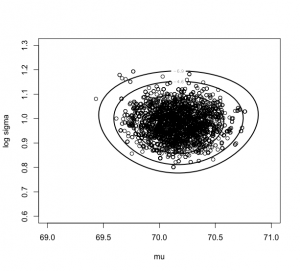
6.8 出力分析の事例
> library(coda)
> library(lattice)
不適切な初期値(μ, log σ)に(65, 1)に、尺度因子を0.2として小さめに設定する。
> start=c(65,1)
> proposal=list(var=fit$var,scale=0.2)
> bayesfit=rwmetrop(groupeddatapost,proposal,start,10000,d)
> dimnames(bayesfit$par)[[2]]=c(“mu”,”log sigma”)
> dimnames(bayesfit$par)[[2]]=c(“mu”,”log sigma”)
> xyplot(mcmc(bayesfit$par[-c(1:2000),]),col=”black”)

> par(mfrow=c(2,1))
> autocorr.plot(mcmc(bayesfit$par[-c(1:2000),]),auto.layout=FALSE)
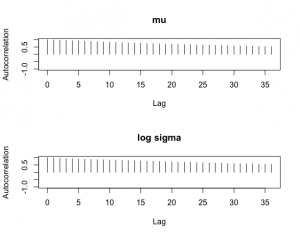
適切な初期値(μ, log σ)に(70, 1), 尺度係数2としてシミュレーション
> start=c(70,1)
> proposal=list(var=fit$var,scale=2)
> bayesfit=rwmetrop(groupeddatapost,proposal,start,10000,d)
> dimnames(bayesfit$par)[[2]]=c(“mu”,”log sigma”)
> xyplot(mcmc(bayesfit$par[-c(1:2000),]),col=”black”)
> par(mfrow=c(2,1))
> autocorr.plot(mcmc(bayesfit$par[-c(1:2000),]),auto.layout=FALSE)
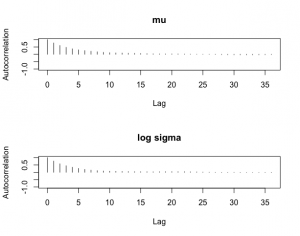
6.9 コーシー誤差によるデータのモデリング
> data(darwin)
> attach(darwin)
> mean(difference)
[1] 21.66667
> log(sd(difference))
[1] 3.65253
> laplace(cauchyerrorpost,c(21.6,3.6),difference)
$mode
[1] 24.701745 2.772619
$var
[,1] [,2]
[1,] 34.9600525 0.3672899
[2,] 0.3672899 0.1378279
$int
[1] -73.2404
$converge
[1] TRUE
> c(24.7-4*sqrt(34.96),24.7+4*sqrt(34.96))
[1] 1.049207 48.350793
> c(2.77-4*sqrt(.138),2.77+4*sqrt(.138))
[1] 1.284066 4.255934
>
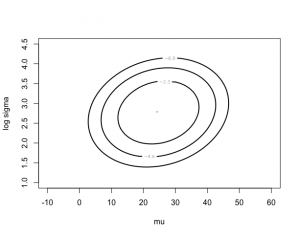
> mycontour(cauchyerrorpost,c(-10,60,1,4.5),difference,
+ xlab=”mu”,ylab=”log sigma”)
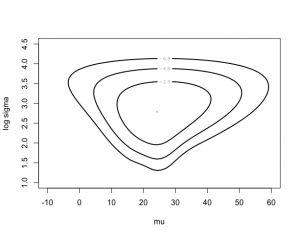
> fitlaplace=laplace(cauchyerrorpost,c(21.6,3.6), difference)
>
> mycontour(lbinorm,c(-10,60,1,4.5),list(m=fitlaplace$mode,
+ v=fitlaplace$var), xlab=”mu”,ylab=”log sigma”)
> proposal=list(var=fitlaplace$var,scale=2.5)
> start=c(20,3)
> m=1000
> s=rwmetrop(cauchyerrorpost,proposal,start,m,difference)
>
> mycontour(cauchyerrorpost,c(-10,60,1,4.5),difference,
+ xlab=”mu”,ylab=”log sigma”)
> points(s$par[,1],s$par[,2])

> proposal=list(var=fitlaplace$var,scale=2.5)
> start=c(20,3)
> m=1000
> s=rwmetrop(cauchyerrorpost,proposal,start,m,difference)
>
> mycontour(cauchyerrorpost,c(-10,60,1,4.5),difference,
+ xlab=”mu”,ylab=”log sigma”)
> points(s$par[,1],s$par[,2])
>
> fitgrid=simcontour(cauchyerrorpost,c(-10,60,1,4.5),difference,
+ 50000)
> proposal=list(var=fitlaplace$var,scale=2.5)
> start=c(20,3)
> fitrw=rwmetrop(cauchyerrorpost,proposal,start,50000,
+ difference)
> proposal2=list(var=fitlaplace$var,mu=t(fitlaplace$mode))
> fitindep=indepmetrop(cauchyerrorpost,proposal2,start,50000,
+ difference)
> fitgibbs=gibbs(cauchyerrorpost,start,50000,c(12,.75),
+ difference)
>
> apply(fitrw$par,2,mean)
[1] 25.538639 2.840757
>
> apply(fitrw$par,2,sd)
[1] 7.2052245 0.3807665
6.10 スタンフォード心臓移植手術のデータ分析
> data(stanfordheart)
>
> start=c(0,3,-1)
> laplacefit=laplace(transplantpost,start,stanfordheart)
> laplacefit
$mode
[1] -0.09210954 3.38385249 -0.72334008
$var
[,1] [,2] [,3]
[1,] 0.172788525 -0.009282308 -0.04995160
[2,] -0.009282308 0.214737054 0.09301323
[3,] -0.049951602 0.093013230 0.06891796
$int
[1] -376.2504
$converge
[1] TRUE
> proposal=list(var=laplacefit$var,scale=2)
> s=rwmetrop(transplantpost,proposal,start,10000,stanfordheart)
> s$accept
[1] 0.1859
> par(mfrow=c(2,2))
> tau=exp(s$par[,1])
> plot(density(tau),main=”TAU”)
> lambda=exp(s$par[,2])
> plot(density(lambda),main=”LAMBDA”)
> p=exp(s$par[,3])
> plot(density(p),main=”P”)

> apply(exp(s$par),2,quantile,c(.05,.5,.95))
[,1] [,2] [,3]
5% 0.5068204 13.25240 0.3064004
50% 0.9769192 29.00776 0.4703718
95% 1.8973773 63.69183 0.7475307
> par(mfrow=c(1,1))
> t=seq(1,240)
> p5=0*t; p50=0*t; p95=0*t
> for (j in 1:240)
+ { S=(lambda/(lambda+t[j]))^p
+ q=quantile(S,c(.05,.5,.95))
+ p5[j]=q[1]; p50[j]=q[2]; p95[j]=q[3]}
> plot(t,p50,type=”l”,ylim=c(0,1),ylab=”Prob(Survival)”,
+ xlab=”time”)
> lines(t,p5,lty=2)
> lines(t,p95,lty=2)
