5.8 棄却サンプリング

棄却サンプリングrejection sampling: 所与の確率分布からランダム標本をシミュレーションする汎用的なアルゴリズム

＜棄却サンプリングのステップ＞
pから標本のシミュレーションが容易である。
密度pは、目的とする事後密度gに近い位置と広がりをもつ。
すべてのθとある定数cについて, g(θ|y)＜=cp(θ)である。

上記の条件を満たす密度pが見つかるとして、次の受理と棄却のアルゴリズムを使ってgから抽出する。
1. pからθを、また単位区間上で一様分布に従う乱数Uを独立にシミュレーションする。
2. U<=g(θ|y)/cp(θ)であればθを密度gからの一つの標本として受理する。さもなければ棄却する。 3. 1と2のアルゴリズムを繰り返して受理されたθが充分な数になるまで繰り返す。 すべてのθについて、g(θ|y)<=cp(θ): cは有界定数(bounding constant) gは対数尺度でプログラム化されるので、定数d=log cを見つけたい。 すべてのθについて、log g(θ|y) - log p(θ)<=d この差の関数betabinT()を作成する。 引数はパラメータthetaとリストdatapar。 dataparは、要素として行列dataとt提案密度のパラメータ(平均、尺度行列、自由度）のリストparを含む。 betabinT=function(theta,datapar) { data=datapar$data tpar=datapar$par d=betabinexch(theta,data)-dmt(theta,mean=c(tpar$m), S=tpar$var,df=tpar$df,log=TRUE) return(d) } ここでの問題に関して、以下のようにt提案密度のパラメータとdataparリストを定義する。 > tpar=list(m=fit$mode,var=2*fit$var,df=4)
> datapar=list(data=cancermortality,par=tpar)

賢明な初期値として、-6.9, 12.4とする。
> start=c(-6.9,12.4)
> fit1=laplace(betabinT,start,datapar)
> fit1$mode
[1] -6.888963 12.421993

最大値dは、θ=(-6.889, 12.422)で与えられた。
dの実際の値はモードでの関数を評価することで決定できる。

> betabinT(fit1$mode,datapar)
[1] -569.2829

rejectsampling()関数を使って棄却サンプリングを実装する。
引数：
対数事後密度を定義する関数logf
tをカバーする密度パラメータtpar
dの最大値dmax
シミュレーションされる候補値の数n
対数密度関数へのデータdata

提案密度からθベクトルをシミュレーションー＞
シミュレーションされた標本に基いてlog gとlog fの値を計算し、受理確率を計算する。
返り値は一様標本が受理確率よりも小さい場合のθのシミュレーション値のみ。

rejectsampling()関数を先に求めたdを使って実行し、提案密度から10,000個のシミュレーションをする。
> theta=rejectsampling(betabinexch,tpar,-569.2813,10000,cancermortality)
> dim(theta)
[1] 2296 2

出力thetaの行数は2406であるので、受理率は2406/10,000=0.24である。

> mycontour(betabinexch,c(-8,-4.5,3,16.5),cancermortality,
+ xlab=”logit eta”,ylab=”log K”)
> points(theta[,1],theta[,2])

棄却サンプリングからシミュレーションした標本を対数事後密度等高線図上にプロット＞期待通り抽出標本がほとんど等高線内部に収まった。

5.9 重点サンプリング
http://www.orsj.or.jp/~wiki/wiki/index.php/重点サンプリング
モンテカルロ法における分散減少法のひとつ. サンプリングすべき領域から, 自然に考えられる本来の確率分布にしたがってサンプルをとるのではなく, 重要と考えられる領域により大きな重みを置いてサンプルをとる方法である. 例えばきわめて稀にしか起きない現象の生起確率を推定したい場合に, この現象が実際よりずっと頻繁に起きるような確率分布にしたがってサンプルをとり, 推測の段階で本来の生起確率に換算するという使い方をする.

関数h(θ)の事後平均は、以下の積分比で与えられる。
E(h(θ)|y) = ∫h(θ)g(θ)f(y|θ)dθ/∫g(θ)f(y|θ)dθ

シミュレーション可能でかつ事後密度gを近似する確率密度pを構成できると仮定する。

E(h(θ)|y) = ∫h(θ)g(θ)f(y|θ)/p(θ)*p(θ)dθ　/　∫g(θ)f(y|θ)/p(θ)*p(θ)dθ

= ∫h(θ)g(θ)w(θ)p(θ)dθ　/　∫w(θ)p(θ)dθ

w(θ) = g(θ)f(y|θ)/p(θ)は重み関数。

hISとseHisを算定できる。

ここでの事例（死亡率）

θ1=logit(η)の値を条件とし、θ2=logKの関数の事後平均を推定する。
g1(θ2|data, θ1)∝K/(1+k)^2　Π　B（Kη+y2, K(1-η）+ nj – yi) / B(Kη, K(1-η)

η = exp(θ1)/(1+exp(θ1)) かつ K=exp(θ2)

θ1=-6.818793を条件とする。
θ2=logK
betabinexch.cond=function (log.K, data)
{
eta = exp(-6.818793)/(1 + exp(-6.818793))
K = exp(log.K)
y = data[, 1]; n = data[, 2]; N = length(y)
logf=0*log.K
for (j in 1:length(y))
logf = logf + lbeta(K * eta + y[j], K * (1 –
eta) + n[j] – y[j]) – lbeta(K * eta, K * (1 – eta))
val = logf + log.K – 2 * log(1 + K)
return(exp(val-max(val)))
}

がん死亡率データlogKの平均値を計算する。
提案密度p, 平均8, 標準偏差2の正規分布
提案密度　位置パラメータ8、尺度パラメータ2, 自由度2のt関数
integrate()関数を使ってlogKの事後密度の正規化定数を求めている。

> I=integrate(betabinexch.cond,2,16,cancermortality)
> par(mfrow=c(2,2))
> curve(betabinexch.cond(x,cancermortality)/I$value,from=3,to=16,
+ ylab=”Density”, xlab=”log K”,lwd=3, main=”Densities”)
> curve(dnorm(x,8,2),add=TRUE)
> legend(“topright”,legend=c(“Exact”,”Normal”),lwd=c(3,1))
> curve(betabinexch.cond(x,cancermortality)/I$value/
+ dnorm(x,8,2),from=3,to=16, ylab=”Weight”,xlab=”log K”,
+ main=”Weight = g/p”)
>
> curve(betabinexch.cond(x,cancermortality)/I$value,from=3,to=16,
+ ylab=”Density”, xlab=”log K”,lwd=3, main=”Densities”)
> curve(1/2*dt(x-8,df=2),add=TRUE)
> legend(“topright”,legend=c(“Exact”,”T(2)”),lwd=c(3,1))
> curve(betabinexch.cond(x,cancermortality)/I$value/
+ (1/2*dt(x-8,df=2)),from=3,to=16, ylab=”Weight”,xlab=”log K”,
+ main=”Weight = g/p”)

5.9.2 提案密度としての多変量t密度
impsanmpling()関数：pがt密度の場合に任意の事後密度に対して重点サンプリングを実現する。
５つの引数を絵耐える。
logf: 事後密度の対数を定義する関数
tpar: t密度のパラメータ値リスト
h: 対象となるh(θ)の関数を定義する関数を指定。
n: シミュレーションの標本サイズ
data: logf関数の定義で使われいてるベクトルないしリストを指定する。

> tpar=list(m=fit$mode,var=2*fit$var,df=4)
> myfunc=function(theta)
+ return(theta[2])
> s=impsampling(betabinexch,tpar,myfunc,10000,cancermortality)
> cbind(s$est,s$se)
[,1] [,2]
[1,] 7.945663 0.01895646

5.10 サンプリング重点リサンプリング（SIR)
> data(cancermortality)
> fit=laplace(betabinexch,c(-7,6),cancermortality)
> tpar=list(m=fit$mode,var=2*fit$var,df=4)
> theta.s=sir(betabinexch,tpar,10000,cancermortality)
> S=bayes.influence(theta.s,cancermortality)

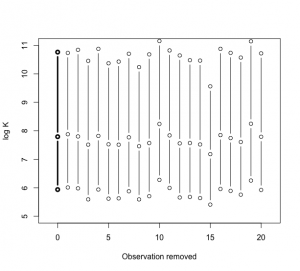
> plot(c(0,0,0),S$summary,type=”b”,lwd=3,xlim=c(-1,21),
+ ylim=c(5,11), xlab=”Observation removed”,ylab=”log K”)
> for (i in 1:20)
+ lines(c(i,i,i),S$summary.obs[i,],type=”b”)