From Baysean Computation with R
5.2 積分を計算する
f(y|θ)からデータyを観測する。ここでθは、パラメータベクトルであり、その事前分布としてg(θ)を割り当てる。
θの事後密度は、
g(θ|y) ∝ g(θ)f(y|θ)
θの関数を推論するために、多変量確率分布を要約することにある。
関数h(θ)の事後平均:E(h(θ)|y)=∫h(θ)g(θ)f(y|θ)dθ / ∫g(θ)f(y|θ)dθ
E(h(θ)|y)∫g(θ)f(y|θ)dθ = ∫h(θ)g(θ)f(y|θ)dθ
E(h(θ)|y) = ∫h(θ)∈Ag(θ)f(y|θ)dθ / ∫g(θ)f(y|θ)dθ
ここでh(θ)が集合Aに入る事後確率は
P(h(θ)∈A|y)=h(θ)∈Ag(θ)f(y|θ)dθ / ∫g(θ)f(y|θ)dθ
積分は関心のあるパラメータの周辺密度の算定にも必要となる。θ=(θ1, θ2)というパラメータがある場合、θ1が関心があるパラメータとすればθ2は局外母数。θ1の周辺事後密度は、結合密度から局外母数を積分消去することで求まる。
g(θ1|y) ∝ ∫g(θ1, θ2|y)dθ2
局外母数とは:「母平均を推定したい場合,母分散には興味がない場合が多いが,このような場合,無関心の母数を局外母数(nuisance parameter)と呼ぶ.推定パラメータ数をmとすると,正規母集団からの平均値の差の検定では,未知母数はμとσの2つで,m=2に相当し,σが局外母数となる」.
->以下の章で、高次元のベイズ問題に適応可能な積分計算の計算方法に焦点が当てられる。
5.3 Rで問題を設定する。
Rでベイズ問題を設定する方法を以下に?明する。
結合事後密度(explicit expression)が書けるものと考える。
以下のように実数化を計る。
分散(正のパラメータ)ー>対数関数変換
割合pー>ロジット変換 logit(p) = log(p/(1-p))
<結合事後密度の対数を定義するR関数を書く>
mylogposterior <- function(theta, data)
{
[対数密度を計算する式をここに定義」
return(val): 事後対数密度の値
}
g(θ|y) ∝ g(θ)f(y|θ)
log(g(θ|y)) ∝ log(g(θ)f(y|θ)) = log(g(θ)) + log(f(y|θ)) = log(g(θ)) + Σlog(f(y1|θ)
平均μで分散σの正規分布からサンプリングすると仮定すると、
θ=(μ, log σ) として、μにはN(10,20)の正規事前分布、log σには平坦な事前分布をあてはめると、
log g(θ|y) = log φ(μ, 10, 20) + Σlog φ(yi; μ, σ)
ここでφ(yi; μ, σ)は平均μ, 標準偏差σの正規密度である。
ひとつのyの要素に対する(μ, σ)の対数尤度を評価する簡単な関数を書くと、
logf <-function(y, mu, sigma)
dnorm(y, mean = mu, sd = sgima, log =TRUE) :注意オプション指定 log=TRUE
対数尤度の項の合計Σ log φ(yi, μ, σ)はsum()関数を使って
sum(logf(data, mu, sigma)
対数事後密度を定義するmylogposterior()関数は、
mylogposterior < function(theta, data)
{
n <- length(data)
mu <- theta[1]; sigma <-exp(theta[2])
logf <-function(y, mu, sigma)
dorm(y, mean = mu, sa = sigma, log =TRUE)
val <- dnorm(mu, mean = 1-, sd = 20, log = TRUE) + sum(logf(data, mu, sigma)
return(val)
}
5.4 過分散に対するベータ・二項モデル
{yi}は、標本サイズ{nj)で共通の死亡率pの独立した二項標本モデルとする。
ただし、頻度{yi}の分散が、確率pの二項モデルの予測より大きくなる過分散を認める。
yiが平均ηで精度パラメータKのベータ二項モデルに従う。
<ベータ二項モデル>
確率 p で表面になるコインを n 回投げたとき、表面となった回数は二項分布に従う。これに対して、表面になる確率 p が定数ではなく、ベータ分布に従う変数としたとき、表面の出る回数はベータ二項分布に従うようになる。
つまり、二項モデルにおける確率pがベータ分布に従うということ。
二項分布に従うと思われていたデータが想定よりも大きな分散をもっていたため,二項分布モデルで 説明できないことがある.これを過分散(over disparsion)という.このようなとき,二項分布 の成功確率 p がベータ分布に従うというモデルが考えられる.この分布をベータ二項分布 という.このように,パラメータに分布を想定したときに生成される 分布を伝染分布(contagious distribution)という.これは,パラメータ分布を事前分布とするベイズ的な考え方 と近いように見えるが,パラメータの事後分布という概念が無いときはベイズではない。
f(yi|η,K) = (nj, yj) (B(Kη+yj), K(1-η)+nj-yi)/(B(Kη, K(1-η))
パラメータに曖昧事前分布を割り当てる。
g(η、K)∝ 1/(η(1−η)* 1/(1+K)^2
すると(η, K)の事後は、比例定数を除いて
g(η, K|data) ∝ 1/(η*(1−η))* 1/(1+K)^2 Π B (Kη+yi, Kη(1-η)+nj-yj) / (B(Kη, K(1-η))
log g(η, K|data) ∝ sum(log B(Kη+yi, K*(1-η)+nj-yj) - log B(Kη、K(1-η)))-log(η)-log(1−η) - 2*(1+K)
betabinexcho0()関数:事後密度の対数を計算する関数 引数は、ηとKの値からなるベクトルで、dataは頻度{yi}と標本サイズ(nj)を列ベクトルとして∈行列。
betabinech0() <- function (theta, data)
{
eta <- theta[1]
K <- theta[2]
y <- data[,1]
n <-data[,2]
N <- length(y)
logf <- function(y, n, K, eta)
lbeta(K * eta + y, K * (1-eta) + n - y) - lbeta(K * eta, K*(1 - eta))
val <- sum(logf(y, n, K, eta)
val <-val - 2*log(1+K) - log(eta) - log(1-eta)
return(val)
}
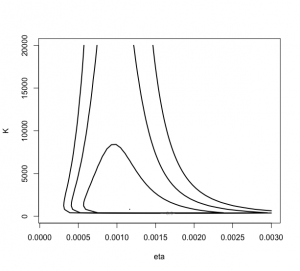
cancermortalityのデータ・セットを読み込んで、対数密度関数betabinexcho0()を指定して
(η,K)の事後密度等高線図を表示させる。
> cancermortality
y n
1 0 1083
2 0 855
3 2 3461
4 0 657
5 1 1208
6 1 1025
7 0 527
8 2 1668
9 1 583
10 3 582
11 0 917
12 1 857
13 1 680
14 1 917
15 54 53637
16 0 874
17 0 395
18 1 581
19 3 588
20 0 383
> mycontour(betabinexch0,c(.0001,.003,1,20000),cancermortality,
+ xlab=”eta”,ylab=”K”)
それぞれのパラメータを次の式の再定式化によって実数直接上の値に変換する。
θ1 = logit(η) = log(η/(1-η)), θ2 = log(K)
(θ1, θ2)の事後密度は
g(θ1, θ2|data) = g(e^θ1/(1+e^θ1), eθ2)*(e^(θ1+θ2)/(1+e^θ1)^2
(e^(θ1+θ2)/(1+e^θ1)^2 はヤコブ行列式
betabinech() <- function (theta, data)
{
eta <- exp(theta[1])/(1+exp(theta[1]))
K <- exp(theta[2])
y <- data[,1]
n <-data[,2]
N <- length(y)
logf <- function(y, n, K, eta)
lbeta(K * eta + y, K * (1-eta) + n - y) - lbeta(K * eta, K*(1 - eta))
val <- sum(logf(y, n, K, eta)
val <-val + theta[2] - 2*log(1+exp(theta[2]))
return(val)
}
> mycontour(betabinexch,c(-8,-4.5,3,16.5),cancermortality,
xlab=”logit eta”,ylab=”log K”)
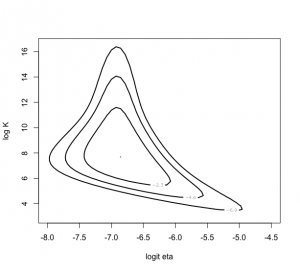
5.5 事後モードに基づく近似
多変量事後分布の要約を行う方法の一つ:モード周辺の密度の挙動を調べる。
θを事前密度g(θ)のパラメータベクトルとする。
サンプリング密度f(y|θ)のデータyを観察する。
θとyの結合密度の対数を検討してみる。
h(θ,y) = log(g(θ)f(y|θ)): 以下この対数密度をh(θ)とする。理由は、観察が終了すれば、θだけがランダム変量だからである。
θの事後モードをθ’とし、対数密度をθ’周辺で二次のテイラー級数に展開する。
h(θ) ≒ h(θ’)+(θ-θ’)’h”(θ’)(θ-θ’)/2: h”(θ’)はモードで評価された対数密度のヘシアン(ヘッセ行列)である。
事後密度は平均がθ’で分散共分散はV=(-h”(θ’))-1の多変量正規密度で近似される。
この近似では結合密度から解析的にθを積分消去可能で、事前予測密度の近似として以下を得る。
f(y) ≒ (2π)^d/2 g(θ’)f(y|θ’)|-h”(θ’)|-1/2: dはθの次元
θ^t = θ^(t-1) – [h”(θ^(t-1))]-1*h'(θ^(t-1))
ここでh'(θ^(t-1)とh”(θ^(t-1)は、それぞれ現在推定されているモードで評価した対数密度の勾配とヘシアン。
これ以外にも事後モードを求めるのに利用できるアルゴリズムがあり、ネルダー・ミード法を用いたoptim()関数がある。
laplace()関数は、optim()関数を呼び出し、ネルダー・ミード法で結合事後モードを求める。
laplace()関数の引数は、結合事後密度を定義する関数、事後モードの初期値、データと、
対数事後密度の定義で使われているパラメータである。
laplace()関数の出力は、4つの要素からなり、要素modeは事後モードθの値、要素varは共分散分散行列V, 要素intは事前予測密度の対数の近似、convergeはアルゴリズムが収束したかどうかを示す。
5.6 事例
ネルダーミード法に初期値の推定値(logit(η), logK)=(-7,6)を与える。
> fit=laplace(betabinexch,c(-7,6),cancermortality)
> fit
$mode
[1] -6.819793 7.576111
$var
[,1] [,2]
[1,] 0.07896568 -0.1485087
[2,] -0.14850874 1.3483208
$int
[1] -570.7743
$converge
[1] TRUE
この結果、事後モードは、(-6.82, 7.58)とわかる。
> npar=list(m=fit$mode,v=fit$var)
> mycontour(lbinorm,c(-8,-4.5,3,16.5),npar,
+ xlab=”logit eta”, ylab=”log K”)
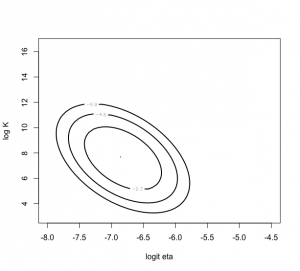
パラメータの90%確率区間を求めると、
> se=sqrt(diag(fit$var))
> fit$mode-1.645*se
[1] -7.282052 5.665982
> fit$mode+1.645*se
[1] -6.357535 9.486239
結果、logit(η)とlogKの90%確率区間は、それぞれ(-7.28, -6.36)と、(5.67, 9.49)となる。
-7.28=log(p/(1-p))
1/e^7.28 = p/(1-p)
e^7.28=1450.988
1/e^7.28 = 0.0006892
p/(1-p)=0.0006892
p=0.0006892(1-p)=0.0006892-0.0006892p
1.0006892p=0.0006892
p=0.0006892/1.0006892=0.0006892 ≒ 0.07%
-6.36=log(p/(1-p))
1/e^6.36 = p/(1-p)
e^6.36=587.246
1/e^6.36 = 0.00170
p/(1-p)=0.00170
p=0.00170(1-p)=0.00170-0.00170p
1.00170p=0.00170
p=0.00170/1.00170=0.001697 ≒ 0.17%
結果として、平均死亡率の90%確率区間は、0.07%-0.17%
5.7 積分計算のためのモンテカルロ法
事後分布を要約する方法のひとつとしてシミュレーションがある。
θの事後密度はE(h(θ)|y) = ∫h(θ)g(θ|y)dθ
ここで事後密度から独立した標本θ1…,θmがシミュレーションできると仮定すれば、
事後平均のモンテカルロ推定値は、以下のように標本平均hとして得られる。
h=Σh(θj)/m
またこの推定値の標準誤差seは
se = √(Σ(h(θj) – h)^2/((m-1)m))
pの事後分布がベータ分布beta(14.26, 23.19)であったアメリカ人学生の十分な睡眠の統計調査の問題を当てはめ、p^2の事後平均をもとめるとすると
> p=rbeta(1000, 14.26, 23.19)
> est=mean(p^2)
> se=sd(p^2)/sqrt(1000)
> c(est,se)
[1] 0.151474735 0.001968181
結果は、E(p^2|data)のモンテカルロ推定値は0.149で、そのシミュレーション誤差は0.002
従ってpは0.389となり、38.9%が睡眠が足りていると推定された。