From Bayesian Computation with R
3.2 平均が既知で分散が未知の正規分布
平均０で未知分散σ^2の正規分布標本とすると、
尤度関数：L(σ^2) ∝ (σ^2)^(-n/2)exp{-Σdi^2/(2σ^2)}

無情報事前密度はp(σ^2)∝1/σ^2とすると、
σ^2事前密度は
g(σ^2|data)∝(σ^2)^(-n/2-1)experience {-v/(2σ^2)}

精度パラメータP=1/σ^2, PはU/v、Uは自由度n-1のカイ二乗分布に従う。

P/v=1/σ^2/ｖのシミュレーション分布をrchisq()関数で作成して、
σ=√（1/P)を計算し、quantile関数で95%確率区間を算定する。

data(footballscores)
> attach(footballscores)
> d = favorite – underdog – spread
> n = length(d)
> v = sum(d^2)
>
> P = rchisq(1000, n)/v
> s = sqrt(1/P)
> hist(s)

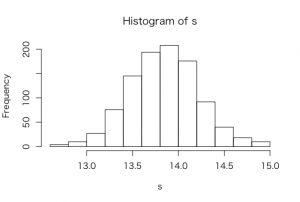
> quantile(s, probs = c(0.025, 0.5, 0.975))
2.5% 50% 97.5%
13.12590 13.83925 14.62322

3.3 心臓移植手術の死亡率を推定する
ある病院での心臓移植手術の死亡率を推定する。
移植手術数e、術後30日以内の死亡数y
手術あたりの死亡率λを推定する。死亡数の期待値はeλである。
死亡数yは平均eλのポアソン分布に従うと想定。
最尤推定値λ=y/e
事前分布としてガンマ分布gamma(α、β）
p(λ）∝ λ(α-1)exp(-βλ）

複数の病院の事前データとして、15174件中16件死亡。　ガンマ事前分布はgamma(16, 15174)
ここである病院のデータが手術件数e, 死亡数yobsとすれば、事後分布もガンマ分布となり、
gamma(α+yobs、β+e)

データが観測される前のyの事前密度は、
f(y)=f(y|λ)g(λ)/g(λ|y)
ここでf(y|λ)はポアソン分布(λe)のサンプリング密度。

f(y)は事前平均値λ=α/βに対して計算する。
>
> alpha=16;beta=15174
> yobs=1; ex=66
> y=0:10
> lam=alpha/beta
> py=dpois(y, lam*ex)*dgamma(lam, shape = alpha,
+ rate = beta)/dgamma(lam, shape= alpha + y,
+ rate = beta + ex)
> cbind(y, round(py, 3))
y
[1,] 0 0.933
[2,] 1 0.065
[3,] 2 0.002
[4,] 3 0.000
[5,] 4 0.000
[6,] 5 0.000
[7,] 6 0.000
[8,] 7 0.000
[9,] 8 0.000
[10,] 9 0.000
[11,] 10 0.000

事後分布はrgamma()関数で1000個の値をシミュレーション
> lambdaA = rgamma(1000, shape = alpha + yobs, rate = beta + ex)

B病院の手術件数1767で、死亡数が４というデータが得られた場合、
> ex = 1767; yobs=4
> y = 0:10
> py = dpois(y, lam * ex) * dgamma(lam, shape = alpha,
+ rate = beta)/dgamma(lam, shape = alpha + y,
+ rate = beta + ex)
> cbind(y, round(py, 3))
y
[1,] 0 0.172
[2,] 1 0.286
[3,] 2 0.254
[4,] 3 0.159
[5,] 4 0.079
[6,] 5 0.033
[7,] 6 0.012
[8,] 7 0.004
[9,] 8 0.001
[10,] 9 0.000
[11,] 10 0.000

> lambdaB = rgamma(1000, shape = alpha + yobs, rate = beta + ex)

> par(mfrow = c(2, 1))
> plot(density(lambdaA), main=”HOSPITAL A”, xlab=”lambdaA”, lwd=3)
> curve(dgamma(x, shape = alpha, rate = beta), add=TRUE)
> legend(“topright”,legend=c(“prior”,”posterior”),lwd=c(1,3))
> plot(density(lambdaB), main=”HOSPITAL B”, xlab=”lambdaB”, lwd=3)
> curve(dgamma(x, shape = alpha, rate = beta), add=TRUE)
> legend(“topright”,legend=c(“prior”,”posterior”),lwd=c(1,3))

3.4 ベイズ法の頑強性
事前の確信に適合する事前分布が多数存在していても、推論がその違いに影響を受けない場合に、ベイズ分析は事前分布の選択に対して「頑強」であるという。

例題）ジョーの知能指数IQの真の値の推定。事前の確信は、ジョーのIQは平均的であり、その事前分布の中央値は100で、90％の確信で80と120の間に位置するとする。

まずは事前分布を正規分布モデルと考えて算出してみる。
つまり、中央値が100で、95%分位点が120である正規分布に適合させる。まずは、この事前分布の平均値と標準偏差を求める。
> quantile1=list(p=.5,x=100); quantile2=list(p=.95,x=120)
> normal.select(quantile1, quantile2)
$mu
[1] 100
$sigma
[1] 12.15914

ジョーは4回IQテストを受けて、そのスコアがy1, y2, y3, y4で、それらの分布がこのIQテストの既知の標準偏差σ=15の正規分布N(θ, σ）に従うと仮定する。観測されるスコアの平均値y_meanは、N(θ, σ/√4)となる。
「精度＝1/分散^2」を利用して、
事後の精度 P1 = 1/τ1^2 は、データの精度Pd=n/σ^2と事前の精度P=1/τ^2の和で表せる。
P1 ＝PD + P = 4/σ^2 + 1/τ^2

事後の標準偏差τ1：
τ1 = 1/√P1 = 1/√（4/σ^2 + 1/τ^2）

θの事後平均μ１は、標本平均はy_meanと事前平均μの加重平均として表現され、その重みは精度に比例する。

μ1 = (y_mean*Pd + μ*P)/(PD + P) = (y_mean(4/σ^2) + μ(1/τ^2))/(4/σ^2+ 1/τ^2)

仮に観測されるテストスコアの平均y_meanが、110, 125, 140であったと三通り考えてみた場合、それぞれの場合について、ジョーの真のIQの事後平均と事後標準偏差を計算する。
> mu = 100
> tau = 12.16
> sigma = 15
> n = 4
> se = sigma/sqrt(4)
> ybar = c(110, 125, 140)
> tau1 = 1/sqrt(1/se^2 + 1/tau^2)
> mu1 = (ybar/se^2 + mu/tau^2) * tau1^2
> summ1=cbind(ybar, mu1, tau1)
> summ1
ybar mu1 tau1
[1,] 110 107.2442 6.383469
[2,] 125 118.1105 6.383469
[3,] 140 128.9768 6.383469

次に、事前分布をT分布であると考えてみる。
位置パラメータμ
尺度パラメータτ
自由度2
のｔ分布を利用する。
中央値μ=100とし、尺度パラメータτはθの95%分位点が120であるとする事前の確信から、120-100=20を選択して、T分布を選ぶ。
P(θ<120) = P(T<20/τ）= 0.95 ここでTha自由度２の標準T変量であり、τ= 20/t2(0.95)。 ここでtv(p)は自由度vのtランダム変数におけるp分位点の値であり、t分位点関数qt()を使って、τを以下のように求める。 > tscale = 20/qt(0.95, 2)
> tscale
[1] 6.849349

> par(mfrow=c(1,1))
> curve(1/tscale*dt((x-mu)/tscale,2),
+ from=60, to=140, xlab=”theta”, ylab=”Prior Density”)
> curve(dnorm(x,mean=mu,sd=tau), add=TRUE, lwd=3)
> legend(“topright”,legend=c(“t density”,”normal density”),
+ lwd=c(1,3))
>

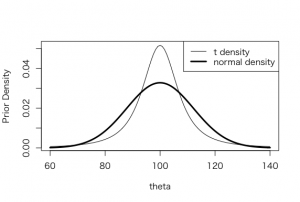
T分布の方が正規分布よりも裾野が平たいので、テストスコアが平均値から極端にずれると事後分布に影響しそうである。

ここで標本のそれぞれについてt事前密度を使って事後密度を計算してみる。
θの事後密度は、

g(θ/y) ∝ φ(y_mean|θ, σ√n)gT(θ|v, μ, τ）

密度を算出する関数がないので、事後密度をカバーする範囲のθ値からなるグリッドを作成して、ｓのグリッド上で、
正規尤度とt事前密度の積を計算し、これらの積和で合計を割ることで確率に変換させる。
（事実上、連続の事後確率密度を、グリッド上の離散分布で近似することである）
ひとつのy_meanに対する計算アルゴリズムnorm.t.compute()を作成し、続いて、sapply()関数で、このアルゴリズムをy_meanの３つの値に適応する。

> norm.t.compute=function(ybar) {
+ theta = seq(60, 180, length = 500)
+ like = dnorm(theta,mean=ybar,sd=sigma/sqrt(n))
+ prior = dt((theta – mu)/tscale, 2)
+ post = prior * like
+ post = post/sum(post)
+ m = sum(theta * post)
+ s = sqrt(sum(theta^2 * post) – m^2)
+ c(ybar, m, s) }
>
> summ2=t(sapply(c(110, 125, 140),norm.t.compute))
> dimnames(summ2)[[2]]=c(“ybar”,”mu1 t”,”tau1 t”)
> summ2
ybar mu1 t tau1 t
[1,] 110 105.2921 5.841676
[2,] 125 118.0841 7.885174
[3,] 140 135.4134 7.973498

２つの方法で求めた結果を結合して、θの事後確率を比較してみる。
> cbind(summ1,summ2)
ybar mu1 tau1 ybar mu1 t tau1 t
[1,] 110 107.2442 6.383469 110 105.2921 5.841676
[2,] 125 118.1105 6.383469 125 118.0841 7.885174
[3,] 140 128.9768 6.383469 140 135.4134 7.973498

> theta=seq(60, 180, length=500)
> normpost = dnorm(theta, mu1[3], tau1)
> normpost = normpost/sum(normpost)
> if (.Platform$OS.type == “unix”) x11() else windows()
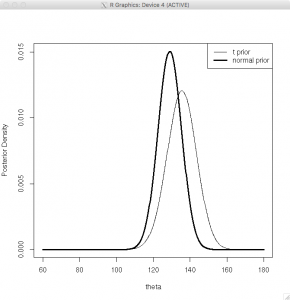
> plot(theta,normpost,type=”l”,lwd=3,ylab=”Posterior Density”)
> like = dnorm(theta,mean=140,sd=sigma/sqrt(n))
> prior = dt((theta – mu)/tscale, 2)
> tpost = prior * like / sum(prior * like)
> lines(theta,tpost)
> legend(“topright”,legend=c(“t prior”,”normal prior”),lwd=c(1,3))
>

3.5 共役事前分布の混合系
curve(.5*dbeta(x, 6, 14) + .5*dbeta(x, 14, 6), from=0, to=1,
xlab=”P”, ylab=”Density”)
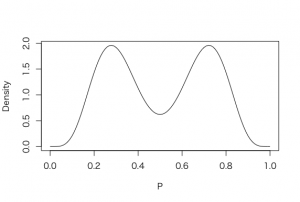binomial.beta.mix()関数は、割合pがベータ事前分布の混合型である場合の事後分布を計算する。

> probs=c(.5,.5)
> beta.par1=c(6, 14)
> beta.par2=c(14, 6)
> betapar=rbind(beta.par1, beta.par2)
> data=c(7,3)
> post=binomial.beta.mix(probs,betapar,data)
> post
$probs
beta.par1 beta.par2
0.09269663 0.90730337

$betapar
[,1] [,2]
beta.par1 13 17
beta.par2 21 9

> curve(post$probs[1]*dbeta(x,13,17)+post$probs[2]*dbeta(x,21,9),
+ from=0, to=1, lwd=3, xlab=”P”, ylab=”DENSITY”)
> curve(.5*dbeta(x,6,12)+.5*dbeta(x,12,6),0,1,add=TRUE)
> legend(“topleft”,legend=c(“Prior”,”Posterior”),lwd=c(1,3))

3.6　コインの偏りについてのベイズ検定
帰無仮説H「コインに偏りがない」、コインの表がでる確率をp=0.5とする。
2 x min{P(Y<=y), P(Y>=y)}　：pが小さい場合、仮説Hを棄却し、コインに偏りがあると結論する。

コインを20回投げて、表が５回以下でる確率は、
> pbinom(5, 20, 0.5)
[1] 0.02069473
p値は、0.021 x 2=0.042となり、有意水準0.05で偏ったコインであるといえる。

ところが、ベイズ的に分析するするとどうなるか？
事前分布g(p)=0.5I(p=0.5) + 0.5I(p≠0.5)g1(p)
I(A）は指示関数で事象Aが真ならば1, 偽ならば0となる。

事後確率分布　g(p|y) = λ(y)I(P=0.5) + (1-λ(y))g1(p|y)
g1は、ベータ密度beta(a+y, a+n-y)で、λ(y)はコインに偏りがないとするモデルの事後確率で
λ(y) = 0.5p(y|0.5)/(0,5p(y|0.5) + 0.5m1(y))

p(y|0.5) : p=0.5の場合のｙのに高密度、m1(y)はベータ密度を利用したyについての事前予測密度。
m1(y) = f(y|p)g1(p) / g1(p|y)

> n = 20
> y = 5
> a = 10
> p = 0.5
> m1 = dbinom(y, n, p) * dbeta(p, a, a)/dbeta(p, a + y, a + n –
+ y)
> lambda = dbinom(y, n, p)/(dbinom(y, n, p) + m1)
> lambda
[1] 0.2802215

> pbetat(p,.5,c(a,a),c(y,n-y))
$bf
[1] 0.3893163

$post
[1] 0.2802215

事前分布のパラメータa=10が、事後分布に影響を与えるかを、prob.fair()関数でlog aの関数として計算する。

> prob.fair=function(log.a)
+ {
+ a = exp(log.a)
+ m2 = dbinom(y, n, p) * dbeta(p, a, a)/
+ dbeta(p, a + y, a + n – y)
+ dbinom(y, n, p)/(dbinom(y, n, p) + m2)
+ }
> n = 20; y = 5; p = 0.5
> curve(prob.fair(x), from=-4, to=5, xlab=”log a”,
+ ylab=”Prob(coin is fair)”, lwd=2)

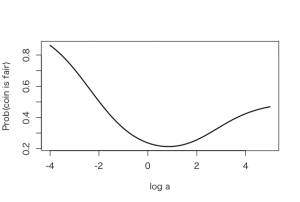
aにかかわらず、グラフに示されたのは確率は0.2以上である。

事象の確率として、コインが5回ちょうどの場合でなく、5回以下の６つの場合で捉えた場合は、
λ(y)= 0.5P0(Y<=5)/(0.5P0(Y<=5)+0.5P1(Y<=5)) > n=20
> y=5
> a=10
> p=.5
> m2=0
> for (k in 0:y)
+ m2=m2+dbinom(k,n,p)*dbeta(p,a,a)/dbeta(p,a+k,a+n-k)
> lambda=pbinom(y,n,p)/(pbinom(y,n,p)+m2)
> lambda
[1] 0.2184649
結果は、先の0.28より少し下がって、「コインに偏りがない」仮説の棄却方向に近づいた。