「ベイズ的思考への誘い」では、アメリカ人の大学生が８時間以上の睡眠を確保しているかどうかについて、ベイズ的統計学的解析が加えられた。
解析は、８時間以上睡眠を取れている場合をs、そうでない場合はfとして、全体の学生数に対するsの比率pを確率として捉えて、つまり「有る無し」の２項分布で、３通りの方法で進められた。

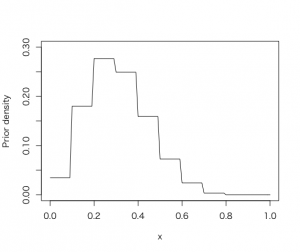
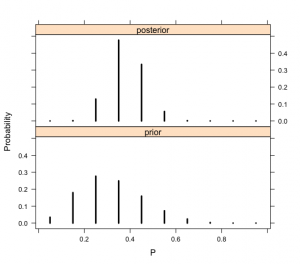
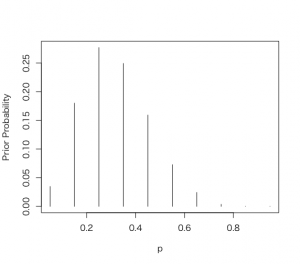
まず、はじめの手法は、調査者の確信に基づき、事前の確率分布として、p値に割合値のリストを作成して、それぞれのp値に対して確信に基づく重みを付けて、「離散事前分布」として、それに対して、大学生27人の調査で11名が睡眠できて、16名が睡眠できていないという結果を受けて、事前の推定分布を修正する方法として、事前分布情報に、調査に基づくベータ密度関数のパラメータ値（11と16)をpdisc()関数に与えて、事後分布を抽出した。pdisc()は、離散分布から事後分布のpを算出する。
———————————–
pdisc {LearnBayes} R Documentation
Posterior distribution for a proportion with discrete priors
Description: Computes the posterior distribution for a proportion for a discrete prior distribution.
Usage: pdisc(p, prior, data)
Arguments
p
vector of proportion values
prior
vector of prior probabilities
data
vector consisting of number of successes and number of failures
Value
vector of posterior probabilities
———————————–

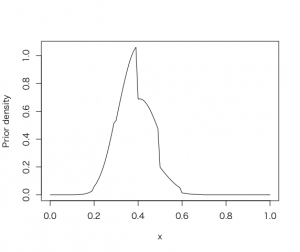
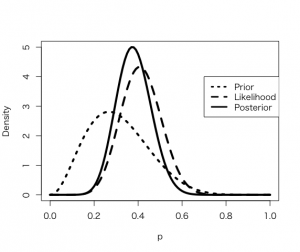
次にベータ事前分布を利用した解析である。ここでは、事前の確信から導かれた分布の中央値と90%分位点の値を利用して、それにフィットする事前ベータ分布のパラメータをbeta.select()関数で決定する。そうなれば、事前ベータ分布の調査によるｓとｆの数値で構成される尤度関数を事前ベータ分布にかけ合わせれば、事後分布もベータ分布となることを利用して、事後のベータ分布のパラメータを決定する。分布はdbeta()関数で求める。要するにこの方法は、ベータ分布の誘導関数はベータ分布であり、事後もベータ分布であることを利用して、算定を極めて簡単にしている点が特徴であろう。

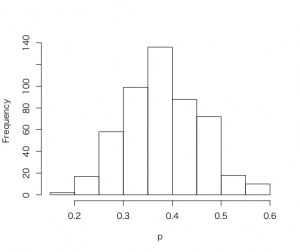
最後の方法は、上記を２方法を合わしたようなものであるが、事前のヒストグラム情報を利用して、まじはhistprio()関数で、事前のヒストグラム分布を事前確率密度に「無理やり＝プロートフォース」に変える。この事前分布に、dbeta()関数を用いてベータ分布の尤度関数を事前のhistprio()関数で得られた事前分布にかけ合わせれば、事後分布が得られるということである。最後に、sample()関数を用いて、復元標本を採取する。