1.
> p = seq(0.0, 1.0, by = 0.125)
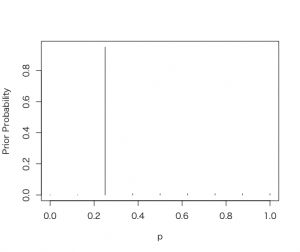
> prior = c(0.001, 0.001, 0.95, 0.008, 0.008, 0.008, 0.008, 0.008, 0.008)
> prior = prior/sum(prior)
> plot(p, prior, type = “h”, ylab=”Prior Probability”)

> data <-c(6, 4) > post <-pdisc(p, prior, data) > round(cbind(p, prior, post), 2)
p prior post
[1,] 0.00 0.00 0.00
[2,] 0.12 0.00 0.00
[3,] 0.25 0.95 0.73
[4,] 0.38 0.01 0.03
[5,] 0.50 0.01 0.08
[6,] 0.62 0.01 0.09
[7,] 0.75 0.01 0.06
[8,] 0.88 0.01 0.01
[9,] 1.00 0.01 0.00
> library(lattice)
> PRIOR=data.frame(“prior”,p,prior)
> POST=data.frame(“posterior”,p,post)
> names(PRIOR)=c(“Type”,”P”,”Probability”)
> names(POST)=c(“Type”,”P”,”Probability”)
> data=rbind(PRIOR,POST)
>
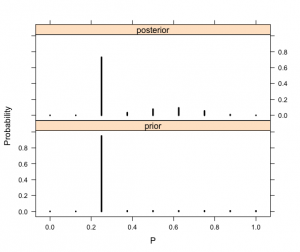
> xyplot(Probability~P|Type,data=data,layout=c(1,2),
+ type=”h”,lwd=3,col=”black”)

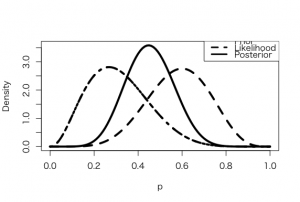
> a <- 3.26 > b <- 7.18 > s <- 6 > f <- 4 > curve(dbeta(x,a+s, b+f), from =0, to = 1, xlab =”p”, ylab = “Density”, lty = 1, lwd =4)
> curve(dbeta(x,s+1, f+1), add=TRUE, lty = 2, lwd =4)
> curve(dbeta(x,a, b), add=TRUE, lty = 4, lwd =4)
> curve(dbeta(x,a, b), add=TRUE, lty = 3, lwd =4)
> legend(.7, 4, c(“Prior”, “Likelihood”, “Posterior”), lty=c(3,2,1), lwd=c(3,3,3))

> 1 – pbeta(0.5, a + s, b + f)
[1] 0.3322116
>
> qbeta(c(0.05, 0.95), a + s, b + f)
[1] 0.2784821 0.6329408
>
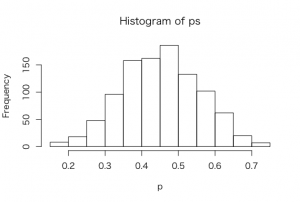
> ps = rbeta(1000, a + s, b + f)
>
> hist(ps,xlab=”p”)
>
> sum(ps >= 0.5)/1000
[1] 0.324
>
> quantile(ps, c(0.05, 0.95))
5% 95%
0.2754209 0.6294736
>

> ab=c(3.26, 7.19)
>
> m=10; ys=0:10
> pred=pbetap(ab, m, ys)
>
> p=rbeta(1000,3.26, 7.19)
>
> y = rbinom(1000, 10, p)
>
> table(y)
y
0 1 2 3 4 5 6 7 8 9 10
62 147 182 182 179 102 80 39 17 8 2
>
> freq=table(y)
> ys=as.integer(names(freq))
> predprob=freq/sum(freq)
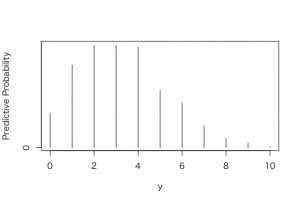
> plot(ys,predprob,type=”h”,xlab=”y”,
+ ylab=”Predictive Probability”)

> dist=cbind(ys,predprob)
>
> covprob=.9
> discint(dist,covprob)
$prob
0
0.934

$set
0 1 2 3 4 5 6
0 1 2 3 4 5 6

2.
> midpt=seq(0.05, 0.95, by=.1)
> midpt
[1] 0.05 0.15 0.25 0.35 0.45 0.55 0.65 0.75 0.85 0.95
> prior = c(1, 2, 3, 4, 5, 5, 4, 3, 2, 1)
> prior=prior/sum(prior)
> curve(histprior(x, midpt, prior), from =0, to =1, ylab = “Prior density”, ylim = c(0,.3))

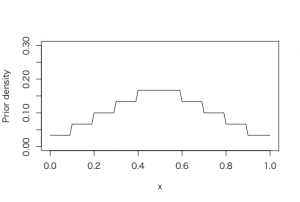
> s = 4
> f = 6
> curve(histprior(x,midpt,prior) * dbeta(x,s+1,f+1),
+ from=0, to=1, ylab=”Posterior density”)

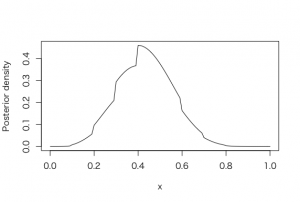
> p = seq(0, 1, length=500)
> post = histprior(p, midpt, prior) *
+ dbeta(p, s+1, f+1)
> post = post/sum(post)
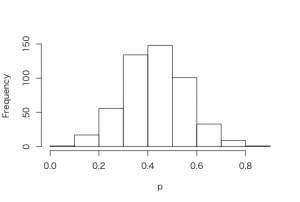
> ps = sample(p, replace = TRUE, prob = post)
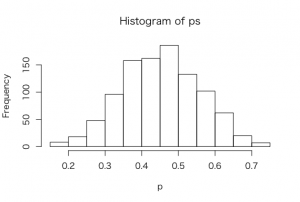
> hist(ps, xlab=”p”, main=””)

3.
a)
> qbeta(c(0.05, 0.95), 1+23, 1+8)
[1] 0.5939430 0.8447224

b)
> 1-pbeta(0.6, 1+23, 1+8)
[1] 0.9425151

c)
> ps <-rbeta(1000, 1+23, 1+8) > hist(ps, xlab = “p”, main =””)

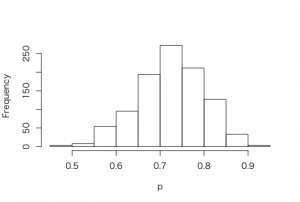
d)
> ps <-rbeta(1000, 1+23, 1+8) > hist(ps, xlab = “p”, main =””)
> y <- rbinom(1000, 10, ps) > table(y)
y
2 3 4 5 6 7 8 9 10
4 16 36 106 149 245 220 163 61
> freq=table(y)
> ys=as.integer(names(freq))
> predprob=freq/sum(freq)
> plot(ys,predprob,type=”h”,xlab=”y”,
+ ylab=”Predictive Probability”)
>
> dist=cbind(ys,predprob)
>
> covprob=.9
> discint(dist,covprob)
$prob
10
0.944

$set
5 6 7 8 9 10
5 6 7 8 9 10

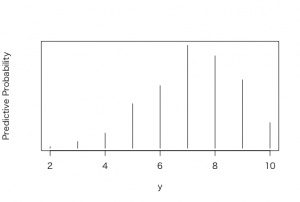
> dist
ys predprob
2 2 0.004
3 3 0.016
4 4 0.036
5 5 0.106
6 6 0.149
7 7 0.245
8 8 0.220
9 9 0.163
10 10 0.061

4.
a)
> p <- c(0.1, 0.2, 0.3, 0.4, 0.5) > prior = c(0.5, 0.2,0.2, 0.05, 0.05)
> prior = prior/sum(prior)
> plot(p, prior, type = “h”, ylab=”Prior Probability”)

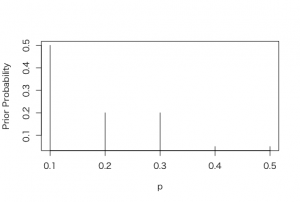
> summary(prior)
Min. 1st Qu. Median Mean 3rd Qu. Max.
0.05 0.05 0.20 0.20 0.20 0.50
> mean(prior)
[1] 0.2
> sd(prior)
[1] 0.1837117

> curve(dbeta(x, s+1, f+1), from =0, to =1, xlab =”p”, ylab =”Density”, lty =1, lwd =4)
> mean <- 3/(3+12) > sigma <- mean*(1-mean)/(3+12+1) > mean
[1] 0.2
> sigma
[1] 0.01
> sd_sum <- sqrt(sigma) > sd_sum
[1] 0.1

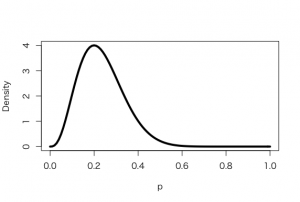
平均値はどちらも0.2だが、ジョーの標準偏差は0.18で、サムは0.1と見積もっている。

b)
まずジョーの事前分布からの分析
>data <- c(3, 12) > post <- pdisc(p, prior, data) > round(cbind(p, prior,post), 2)
p prior post
[1,] 0.1 0.50 0.42
[2,] 0.2 0.20 0.33
[3,] 0.3 0.20 0.22
[4,] 0.4 0.05 0.02
[5,] 0.5 0.05 0.00
> m <-12; ys <-0:12 > pred <-pdiscp(p, prior, m, ys) > round(cbind(0:12, pred), 3)
pred
[1,] 0 0.158
[2,] 1 0.245
[3,] 2 0.209
[4,] 3 0.148
[5,] 4 0.100
[6,] 5 0.065
[7,] 6 0.039
[8,] 7 0.021
[9,] 8 0.010
[10,] 9 0.004
[11,] 10 0.001
[12,] 11 0.000
[13,] 12 0.000
結果は、1か２名。
次にサムのベータ事前分布
> p <-rbeta(1000, 3, 12) > y <-rbinom(1000, 12, p) > table(y)
y
0 1 2 3 4 5 6 7 8 9
148 208 219 171 111 71 44 16 10 2
> freq <-table(y) > ys <- as.integer(names(freq)) > predprob <- freq/sum(freq) > plot(ys, predprob, type =”h”, xlab=”y”, ylab=”Predictive Probability”)

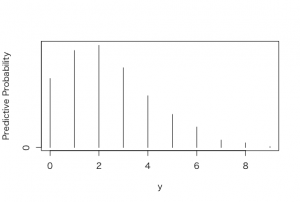
> dist <-cbind(ys, predprob) > dist
ys predprob
0 0 0.148
1 1 0.208
2 2 0.219
3 3 0.171
4 4 0.111
5 5 0.071
6 6 0.044
7 7 0.016
8 8 0.010
9 9 0.002

結果は、１名か２名で、ジョーと同じ結果となった。

5.
a)
> mu <- c(20, 30, 40, 50, 60 , 70) > prior <- c(0.1, 0.15, 0.25, 0.25, 0.15, 0.1) b) > y <- c(38.6, 42.4, 57.5, 40.5, 51.7, 67.1, 33.4, 60.9, 64.1, 40.1, 40.7, 6.4) > ybar <- mean(y) > y
[1] 38.6 42.4 57.5 40.5 51.7 67.1 33.4 60.9 64.1 40.1 40.7 6.4
> ybar
[1] 45.28333

c)
> like <- exp(-12/(2*10^2)*(ybar-mu)^2) > post <- prior * like/sum(prior * like) > plot(post)
> hist(post, xlab =”p”, ylab = “”)
> plot(mu, post, type=”h”, xlab =”y”, ylab = “Predctive Probability”)

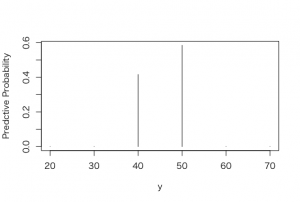
> dist <- cbind(mu, post) > dist
mu post
[1,] 20 1.954479e-17
[2,] 30 1.091063e-06
[3,] 40 4.158078e-01
[4,] 50 5.841881e-01
[5,] 60 3.025731e-06
[6,] 70 1.069871e-16
> covprob <-.8 > discint(dist, covprob)
$prob
[1] 0.9999959

$set
[1] 40 50

80％信頼区間は、40cm-50cmという結果。

6.
a)
p <- cbind(0.5, 1, 1.5, 2, 2.5, 3) > prior <- cbind(0.1, 0.2, 0.3, 0.2, 0.15, 0.05) > prior = prior/sum(prior)
> like <- exp(-6*p)*(6*p)^12 > post <- prior*like > plot(p, post, type=”h”, xlab =”y”, ylab = “Predctive Probability”)
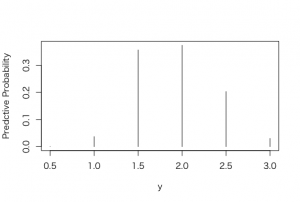
> predprob <- post/sum(post) > plot(p, predprob, type=”h”, xlab =”y”, ylab = “Predctive Probability”)

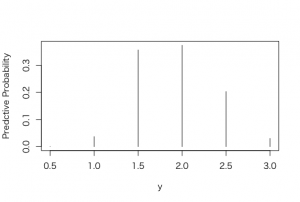
b)
> post2 <- exp(-7*p)*predprob > plot(p, post2, type=”h”, xlab =”y”, ylab = “Predctive Probability”)
> predprob2 <- post2/sum(post2) > plot(p, predprob2, type=”h”, xlab =”y”, ylab = “Predctive Probability”)

> post2 <- exp(-7*p)*predprob > plot(p, post2, type=”h”, xlab =”y”, ylab = “Predctive Probability”)

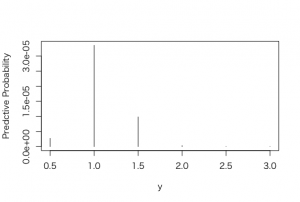
> post2_sum <- sum(post2) > post2_sum
[1] 4.640932e-05
>