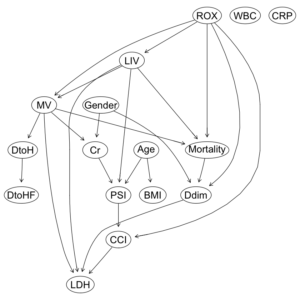
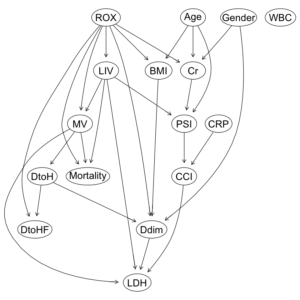
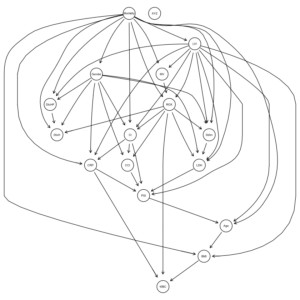
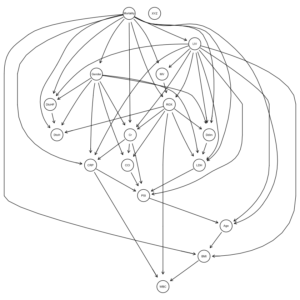
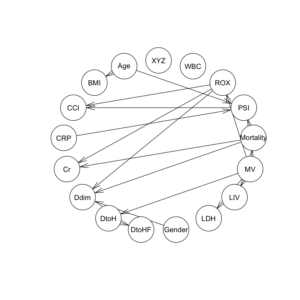
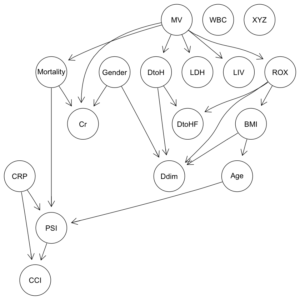
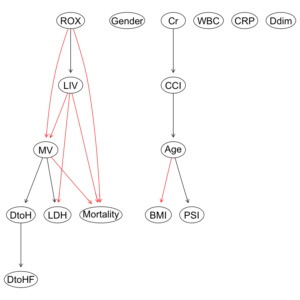
COVID-19重症呼吸不全患者に対するHNFC/MVの治療選択に対する影響因子:因果分析=>ベイジアンネットワーク 有向非巡回グラフ(DAG)の作成
16データでの解析、ROXの閾値6.1と4.88での人工呼吸率&死亡率の比較、推定
by R 4.05 Oct 28, 2022
全59件のデータ:ROX閾値と人工呼吸頻度(率)と死亡頻度(率)の関係
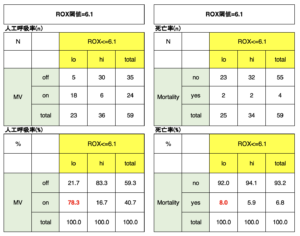
59件のデータから得られた尤度としては、
人工呼吸率は、ROX<=6.1では78.3%、ROX<=4.88では90.0%、
死亡率は、ROX<=6.1では8.0%、ROX<=4.88では10.0%であった。
この値が推測の目安となるであろう。
データは16項目(離散値:3項目と、連続値:13項目の混合)
MV:離散値
ROX:連続値
LIV:連続値
Gender:離散値
Age:連続値
BMI:連続値
WBC:連続値
Cr:連続値
CRP:連続値
LDH:連続値
Ddim:連続値
PSI:連続値
CCI:連続値
DtoH:連続値
DtoHF:連続値
Mortality:離散値
以下、ROXの閾値を6.1としたデータセット#1と、4.88としたデータセット#2と平行して解析を進めて、
比較検討する。
|
1 2 3 4 |
df <- read.csv("data_f16R.csv", header=TRUE, fileEncoding="utf-8") df1 <- df df2 <- df df1 |
A data.frame: 59 × 16
MV ROX LIV Gender Age BMI WBC Cr CRP LDH Ddim PSI CCI DtoH DtoHF Mortality
off 9.9 29.2 male 53 34.8 12600 1.0 9.4 327 0.6 53 1 4 9 no
off 11.4 25.0 female 74 25.9 5500 0.8 14.7 459 1.4 114 4 9 9 no
off 9.3 22.2 female 43 24.9 7600 0.6 12.3 375 1.1 43 0 8 8 no
off 6.7 22.5 female 72 18.5 19500 0.7 4.9 378 0.7 72 1 11 10 no
………
ROXとLIVに関しては、閾値を設定して、High(hi)とLow(lo)の離散値へ変換
ROXの閾値は6.1と4.88, LIVの閾値は35.5とする。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
ROX_threshold_1 = 6.1 LIV_threshold_1 = 35.5 df1$ROX[df1$ROX <= ROX_threshold_1] <- "lo" df1$ROX[df1$ROX != "lo"] <- "hi" df1$LIV[df1$LIV <= LIV_threshold_1] <- "lo" df1$LIV[df1$LIV != "lo"] <- "hi" df1 ROX_threshold_2 = 4.88 LIV_threshold_2 = 35.5 df2$ROX[df2$ROX <= ROX_threshold_2] <- "lo" df2$ROX[df2$ROX != "lo"] <- "hi" df2$LIV[df2$LIV <= LIV_threshold_2] <- "lo" df2$LIV[df2$LIV != "lo"] <- "hi" df2 |
A data.frame: 59 × 16
MV ROX LIV Gender Age BMI WBC Cr CRP LDH Ddim PSI CCI DtoH DtoHF Mortality
off hi lo male 53 34.8 12600 1.0 9.4 327 0.6 53 1 4 9 no
off hi lo female 74 25.9 5500 0.8 14.7 459 1.4 114 4 9 9 no
off hi lo female 43 24.9 7600 0.6 12.3 375 1.1 43 0 8 8 no
off hi lo female 72 18.5 19500 0.7 4.9 378 0.7 72 1 11 10 no
off lo lo male 59 24.8 9500 0.6 14.2 475 36.0 79 1 13 12 no
…………………
tidyverseライブラリを呼んで離散データの文字列データセットをカテゴリカルデータセットに変換する。
|
1 2 |
#install.packages("tidyverse") library("tidyverse") |
データフレームの離散値カテゴリーをカテゴリカル・データへ変換
|
1 2 3 4 5 6 |
df1F <- df1 %>% mutate(MV = factor(MV, levels = c("off", "on"))) df1F <- df1F %>% mutate(Gender = factor(Gender, levels = c("male", "female"))) df1F <- df1F %>% mutate(Mortality = factor(Mortality, levels = c("no", "yes"))) df1F <- df1F %>% mutate(ROX = factor(ROX, levels = c("hi", "lo"))) df1F <- df1F %>% mutate(LIV = factor(LIV, levels = c("hi", "lo"))) df1F |
A data.frame: 59 × 16
MV ROX LIV Gender Age BMI WBC Cr CRP LDH Ddim PSI CCI DtoH DtoHF Mortality
off hi lo male 53 34.8 12600 1.0 9.4 327 0.6 53 1 4 9 no
off hi lo female 74 25.9 5500 0.8 14.7 459 1.4 114 4 9 9 no
off hi lo female 43 24.9 7600 0.6 12.3 375 1.1 43 0 8 8 no
off hi lo female 72 18.5 19500 0.7 4.9 378 0.7 72 1 11 10 no
off lo lo male 59 24.8 9500 0.6 14.2 475 36.0 79 1 13 12 no
…………
|
1 2 3 4 5 6 |
df2F <- df2 %>% mutate(MV = factor(MV, levels = c("off", "on"))) df2F <- df2F %>% mutate(Gender = factor(Gender, levels = c("male", "female"))) df2F <- df2F %>% mutate(Mortality = factor(Mortality, levels = c("no", "yes"))) df2F <- df2F %>% mutate(ROX = factor(ROX, levels = c("hi", "lo"))) df2F <- df2F %>% mutate(LIV = factor(LIV, levels = c("hi", "lo"))) df2F |
A data.frame: 59 × 16
MV ROX LIV Gender Age BMI WBC Cr CRP LDH Ddim PSI CCI DtoH DtoHF Mortality
off hi lo male 53 34.8 12600 1.0 9.4 327 0.6 53 1 4 9 no
off hi lo female 74 25.9 5500 0.8 14.7 459 1.4 114 4 9 9 no
off hi lo female 43 24.9 7600 0.6 12.3 375 1.1 43 0 8 8 no
off hi lo female 72 18.5 19500 0.7 4.9 378 0.7 72 1 11 10 no
……….
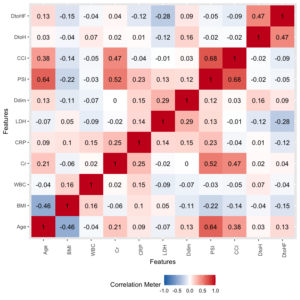
ヒートマップ作成
|
1 2 |
#install.packages("DataExplorer") library("DataExplorer") |
|
1 |
plot_correlation(df, type = "all") |
|
1 |
plot_correlation(df1F, type = "c") |
|
1 |
plot_correlation(df2F, type = "c") |
1. bnlearn解析:その1:Hill-Climb法
|
1 2 3 4 5 6 |
#install.packages("bnlearn") library(bnlearn) #install.packages("BiocManager") #BiocManager::install("Rgraphviz") library(Rgraphviz) |
まずは、空のDAG構造を生成する。
|
1 2 |
dag1 = empty.graph(colnames(df1F)) dag2 = empty.graph(colnames(df2F)) |
|
1 |
graphviz.plot(dag1, layout = "fdp", shape = "ellipse") |
|
1 |
graphviz.plot(dag2, layout = "fdp", shape = "ellipse") |
ブラックリスト作成
|
1 2 3 4 5 6 |
bl2 = tiers2blacklist(list("Gender", "Age")) bl2 = matrix(c("Gender", "Age", "Mortality","PSI", "Mortality", "Cr"), ncol = 2, byrow = TRUE, dimnames = list(NULL, c("from", "to"))) bl2 |
A matrix: 3 × 2 of type chr
from to
Gender Age
Mortality PSI
Mortality Cr
ホワイトリスト作成
|
1 2 3 4 5 6 7 8 9 10 |
wl2 = matrix(c("ROX", "MV", "LIV", "MV", "LIV", "LDH", "Age", "BMI", "MV", "Mortality", "ROX", "Mortality", "LIV", "Mortality"), ncol = 2, byrow = TRUE, dimnames = list(NULL, c("from", "to"))) wl2 |
A matrix: 7 × 2 of type chr
from to
ROX MV
LIV MV
LIV LDH
Age BMI
MV Mortality
ROX Mortality
LIV Mortality
Hill-Climb法の関数hc()で、データセットと、ホワイトリスト、ブラックリストを指定して、dag構造を構築する。
|
1 2 |
dag1 = hc(df1F, whitelist = wl2, blacklist = bl2) dag1 |
Bayesian network learned via Score-based methods
model:
[ROX][Gender][Age][WBC][CRP][LIV|ROX][BMI|Age][MV|ROX:LIV][Cr|MV:Gender]
[DtoH|MV][Mortality|MV:ROX:LIV][Ddim|ROX:Gender:Mortality][PSI|LIV:Age:Cr]
[DtoHF|DtoH][CCI|ROX:PSI][LDH|MV:LIV:Ddim:CCI]
nodes: 16
arcs: 23
undirected arcs: 0
directed arcs: 23
average markov blanket size: 4.38
average neighbourhood size: 2.88
average branching factor: 1.44
learning algorithm: Hill-Climbing
score: BIC (cond. Gauss.)
penalization coefficient: 2.038769
tests used in the learning procedure: 462
optimized: TRUE
|
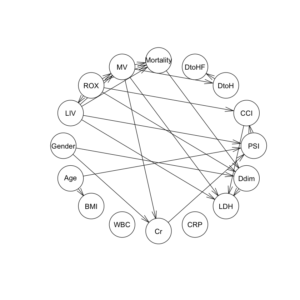
1 |
graphviz.plot(dag1, shape = "ellipse", highlight = list(arcs = wl2)) |
|
1 2 |
dag2 = hc(df2F, whitelist = wl2, blacklist = bl2) dag2 |
Bayesian network learned via Score-based methods
model:
[ROX][Gender][Age][WBC][CRP][LIV|ROX][BMI|ROX:Age][Cr|ROX:Gender:Age]
[MV|ROX:LIV][PSI|LIV:Age:Cr][CCI|CRP:PSI][DtoH|MV][Mortality|MV:ROX:LIV]
[Ddim|ROX:Gender:BMI:DtoH][DtoHF|ROX:DtoH][LDH|MV:LIV:Ddim:CCI]
nodes: 16
arcs: 27
undirected arcs: 0
directed arcs: 27
average markov blanket size: 5.25
average neighbourhood size: 3.38
average branching factor: 1.69
learning algorithm: Hill-Climbing
score: BIC (cond. Gauss.)
penalization coefficient: 2.038769
tests used in the learning procedure: 521
optimized: TRUE
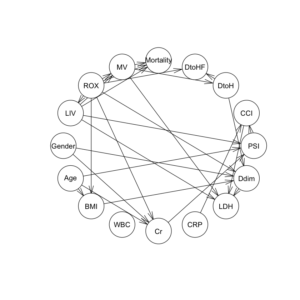
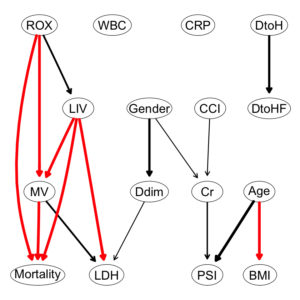
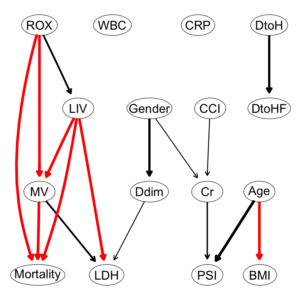
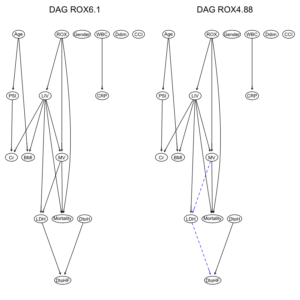
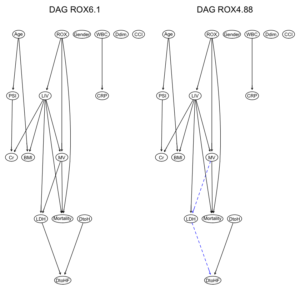
ROXの閾値が6.1と4.88と異なるだけで、ROXの”hi”, “lo”の比率変化が、DAGの構造に影響したことがわかる。
ROX閾値6.1ではarcは23個だが、一方、ROX閾値4.88では、arcは27個に増加している。
|
1 |
graphviz.plot(dag2, shape = "ellipse", highlight = list(arcs = wl2)) |
|
1 |
plot(dag1) |
|
1 |
plot(dag2) |
|
1 |
graphviz.plot(dag1, shape = "ellipse") |
|
1 |
graphviz.plot(dag2, shape = "ellipse") |
2つのデータセット由来のDAG構造を比較してみる。
|
1 2 |
par(mfrow = c(1,2)) graphviz.compare(dag1, dag2, shape = "ellipse", main = c("DAG ROX6.1", "DAG ROX4.88")) |
推定1
|
1 2 3 4 5 |
fitted.simpler1 = bn.fit(dag1, df1F) fitted.simpler1 fitted.simpler2 = bn.fit(dag2, df2F) fitted.simpler2 |
|
1 2 3 4 |
print("P(MV=on, ROX=Low)") round(cpquery(fitted.simpler1, event = (MV == "on"), evidence = (ROX == "lo")), digits = 3) print("P(MV=on, ROX=Low)") round(cpquery(fitted.simpler2, event = (MV == "on"), evidence = (ROX == "lo")), digits = 3) |
[1] “P(MV=on, ROX=Low)”
0.718
[1] “P(MV=on, ROX=Low)”
0.9
尤度は、ROX<=6.1では人工呼吸率は78.3%、ROX<=4.88では人工呼吸率は90.0% であったので、ほぼ近い。
|
1 2 3 4 |
print("P(MV=on, ROX=High)") round(cpquery(fitted.simpler1, event = (MV == "on"), evidence = (ROX == "hi")), digits = 3) print("P(MV=on, ROX=High)") round(cpquery(fitted.simpler2, event = (MV == "on"), evidence = (ROX == "hi")), digits = 3) |
[1] “P(MV=on, ROX=High)”
0.173
[1] “P(MV=on, ROX=High)”
0.304
|
1 2 3 4 |
print("P(Mortality=yes, ROX=Low)") round(cpquery(fitted.simpler1, event = (Mortality == "yes"), evidence = (ROX == "lo")), digits = 3) print("P(Mortality=yes, ROX=Low)") round(cpquery(fitted.simpler2, event = (Mortality == "yes"), evidence = (ROX == "lo")), digits = 3) |
[1] “P(Mortality=yes, ROX=Low)”
0.087
[1] “P(Mortality=yes, ROX=Low)”
0.094
尤度は、ROX<=6.1では死亡率は8.0%、ROX<=4.88では人工呼吸率は10.0% であったのでほぼ近いところ。
|
1 2 3 4 |
print("P(Mortality=yes, ROX=High)") round(cpquery(fitted.simpler1, event = (Mortality == "yes"), evidence = (ROX == "hi")), digits = 3) print("P(Mortality=yes, ROX=High)") round(cpquery(fitted.simpler2, event = (Mortality == "yes"), evidence = (ROX == "hi")), digits = 3) |
[1] “P(Mortality=yes, ROX=High)”
0.059
[1] “P(Mortality=yes, ROX=High)”
0.058
|
1 2 3 4 |
print("P(MV=on, ROX=Low, LIV=High)") round(cpquery(fitted.simpler1, event = (MV == "on"), evidence = ((ROX == "lo") & (LIV == "hi"))), digits = 3) print("P(MV=on, ROX=Low, LIV=High)") round(cpquery(fitted.simpler2, event = (MV == "on"), evidence = ((ROX == "lo") & (LIV == "hi"))), digits = 3) |
[1] “P(MV=on, ROX=Low, LIV=High)”
0.929
[1] “P(MV=on, ROX=Low, LIV=High)”
1
|
1 2 3 4 |
print("P(MV=off, ROX=Low, LIV=High)") round(cpquery(fitted.simpler1, event = (MV == "off"), evidence = ((ROX == "lo") & (LIV == "hi"))), digits = 3) print("P(MV=off, ROX=Low, LIV=High)") round(cpquery(fitted.simpler2, event = (MV == "off"), evidence = ((ROX == "lo") & (LIV == "hi"))), digits = 3) |
[1] “P(MV=off, ROX=Low, LIV=High)”
0.077
[1] “P(MV=off, ROX=Low, LIV=High)”
0
|
1 2 3 4 |
print("P(MV=ON, ROX=Low, LIV=High, LDH=High)") round(cpquery(fitted.simpler1, event = (MV == "on"), evidence = ((ROX == "lo") & (LIV == "hi") & (LDH > mean(df1F$LDH)))), digits = 3) print("P(MV=ON, ROX=Low, LIV=High, LDH=High)") round(cpquery(fitted.simpler2, event = (MV == "on"), evidence = ((ROX == "lo") & (LIV == "hi") & (LDH > mean(df2F$LDH)))), digits = 3) |
[1] “P(MV=ON, ROX=Low, LIV=High, LDH=High)”
0.946
[1] “P(MV=ON, ROX=Low, LIV=High, LDH=High)”
1
|
1 2 3 4 |
print("P(MV=OFF, ROX=Low, LIV=High, LDH=High)") round(cpquery(fitted.simpler1, event = (MV == "off"), evidence = ((ROX == "lo") & (LIV == "hi") & (LDH > mean(df1F$LDH)))), digits = 3) print("P(MV=OFF, ROX=Low, LIV=High, LDH=High)") round(cpquery(fitted.simpler2, event = (MV == "off"), evidence = ((ROX == "lo") & (LIV == "hi") & (LDH > mean(df2F$LDH)))), digits = 3) |
[1] “P(MV=OFF, ROX=Low, LIV=High, LDH=High)”
0.058
[1] “P(MV=OFF, ROX=Low, LIV=High, LDH=High)”
0
|
1 2 3 4 |
print("P(MV=ON, ROX=Low, LIV=High, LDH=High, Age=High)") round(cpquery(fitted.simpler1, event = (MV == "on"), evidence = ((ROX == "lo") & (LIV == "hi") & (LDH > mean(df1F$LDH)) & (Age > mean(df1F$Age)))), digits = 3) print("P(MV=ON, ROX=Low, LIV=High, LDH=High, Age=High)") round(cpquery(fitted.simpler2, event = (MV == "on"), evidence = ((ROX == "lo") & (LIV == "hi") & (LDH > mean(df2F$LDH)) & (Age > mean(df2F$Age)))), digits = 3) |
[1] “P(MV=ON, ROX=Low, LIV=High, LDH=High, Age=High)”
0.92
[1] “P(MV=ON, ROX=Low, LIV=High, LDH=High, Age=High)”
1
|
1 2 3 4 |
print("P(MV=OFF, ROX=Low, LIV=High, LDH=High, Age=High)") round(cpquery(fitted.simpler1, event = (MV == "off"), evidence = ((ROX == "lo") & (LIV == "hi") & (LDH >mean(df1F$LDH)) & (Age> mean(df1F$Age)))), digits = 3) print("P(MV=OFF, ROX=Low, LIV=High, LDH=High, Age=High)") round(cpquery(fitted.simpler2, event = (MV == "off"), evidence = ((ROX == "lo") & (LIV == "hi") & (LDH >mean(df2F$LDH)) & (Age> mean(df2F$Age)))), digits = 3) |
ベイジアン ネットワークの等価クラスと v 構造を見つけ、モラルグラフを構築するか、等価クラスの一貫した拡張を作成。
※グラフ理論では、有向非巡回グラフの同等の無向形式を見つけるためにモラルグラフが使用される。これはジャンクションツリーアルゴリズムの重要なステップであり、グラフィカルモデルでの信頼度の伝播に使用される。
したがって、以cpdagで作成したグラフでは、有向、無向Arcが混在する。
|
1 |
cpdag(dag1) |
Bayesian network learned via Score-based methods
model:
[partially directed graph]
nodes: 16
arcs: 23
undirected arcs: 7
directed arcs: 16
average markov blanket size: 4.38
average neighbourhood size: 2.88
average branching factor: 1.00
learning algorithm: Hill-Climbing
score: BIC (cond. Gauss.)
penalization coefficient: 2.038769
tests used in the learning procedure: 462
optimized: TRUE
|
1 |
graphviz.plot(cpdag(dag1), shape = "ellipse", highlight = list(arcs = wl2)) |
|
1 |
cpdag(dag2) |
Bayesian network learned via Score-based methods
model:
[partially directed graph]
nodes: 16
arcs: 27
undirected arcs: 6
directed arcs: 21
average markov blanket size: 5.25
average neighbourhood size: 3.38
average branching factor: 1.31
learning algorithm: Hill-Climbing
score: BIC (cond. Gauss.)
penalization coefficient: 2.038769
tests used in the learning procedure: 521
optimized: TRUE
|
1 |
graphviz.plot(cpdag(dag2), shape = "ellipse", highlight = list(arcs = wl2)) |
|
1 2 |
par(mfrow = c(1,2)) graphviz.compare(cpdag(dag1), cpdag(dag2), shape = "ellipse", main = c("DAG ROX6.1", "DAG ROX4.88")) |
2. bnlearn解析:その2:続けてブートストラップ法
|
1 2 |
str.raw1_1 = boot.strength(df1F, R = 200, algorithm = "hc", algorithm.args = list(whitelist = wl2, blacklist = bl2)) attr(str.raw1_1, "threshold") |
0.5
|
1 2 |
str.raw1_2 = boot.strength(df2F, R = 200, algorithm = "hc", algorithm.args = list(whitelist = wl2, blacklist = bl2)) attr(str.raw1_2, "threshold") |
0.5
|
1 2 |
avg.df1_1 = averaged.network(str.raw1_1) strength.plot(avg.df1_1, str.raw1_1, shape = "ellipse", highlight = list(arcs = wl2)) |
|
1 2 |
avg.df1_2 = averaged.network(str.raw1_2) strength.plot(avg.df1_2, str.raw1_2, shape = "ellipse", highlight = list(arcs = wl2)) |
2つのDAGを比較する。
|
1 2 |
par(mfrow = c(1,2)) graphviz.compare(avg.df1_1, avg.df1_2, shape = "ellipse", main = c("DAG ROX6.1", "DAG ROX4.88")) |
|
1 2 |
avg.raw.full1_1 = averaged.network(str.raw1_1) avg.raw.full1_2 = averaged.network(str.raw1_2) |
|
1 |
strength.plot(avg.raw.full1_1, str.raw1_1, shape = "ellipse", highlight = list(arcs = wl2)) |
|
1 |
strength.plot(avg.raw.full1_2, str.raw1_2, shape = "ellipse", highlight = list(arcs = wl2)) |
2つのDAGを比較する。
|
1 2 |
par(mfrow = c(1,2)) graphviz.compare(avg.raw.full1_1, avg.raw.full1_2, shape = "ellipse", main = c("DAG ROX6.1", "DAG ROX4.88")) |
推測2
|
1 2 |
fitted_f16_1 = bn.fit(avg.raw.full1_1, data = df1F) fitted_f16_2 = bn.fit(avg.raw.full1_2, data = df2F) |
|
1 2 3 |
# MV:on, ROX:low round(cpquery(fitted_f16_1, event = (MV == "on"), evidence = (ROX == "lo")), digits = 3) round(cpquery(fitted_f16_2, event = (MV == "on"), evidence = (ROX == "lo")), digits = 3) |
0.727
0.91
尤度は、ROX<=6.1では人工呼吸率は78.3%、ROX<=4.88では人工呼吸率は90.0% であったので、ほぼ近い。
|
1 2 3 |
# MV:OFF, ROX:hi round(cpquery(fitted_f16_1, event = (MV == "on"), evidence = (ROX == "hi")), digits = 3) round(cpquery(fitted_f16_2, event = (MV == "on"), evidence = (ROX == "hi")), digits = 3) |
0.181
0.306
|
1 2 3 |
# MV:OFF, ROX:hi round(cpquery(fitted_f16_1, event = (MV == "off"), evidence = (ROX == "hi")), digits = 3) round(cpquery(fitted_f16_2, event = (MV == "off"), evidence = (ROX == "hi")), digits = 3) |
0.82
0.694
|
1 2 3 |
# MV:OFF, ROX:low round(cpquery(fitted_f16_1, event = (MV == "off"), evidence = (ROX == "lo")), digits = 3) round(cpquery(fitted_f16_2, event = (MV == "off"), evidence = (ROX == "lo")), digits = 3) |
0.276
0.1
|
1 2 3 |
# Mortality:yes, MV:on round(cpquery(fitted_f16_1, event = (Mortality == "yes"), evidence = (MV == "on")), digits = 3) round(cpquery(fitted_f16_2, event = (Mortality == "yes"), evidence = (MV == "on")), digits = 3) |
0.159
0.164
|
1 2 3 |
# Mortality:yes, ROX:low round(cpquery(fitted_f16_1, event = (Mortality == "yes"), evidence = (ROX == "lo")), digits = 3) round(cpquery(fitted_f16_2, event = (Mortality == "yes"), evidence = (ROX == "lo")), digits = 3) |
0.077
0.1
尤度は、ROX<=6.1では死亡率は8.0%、ROX<=4.88では人工呼吸率は10.0% であったのでほぼ近いところ。
|
1 2 3 |
# Mortality:yes, LIV:hi round(cpquery(fitted_f16_1, event = (Mortality == "yes"), evidence = (LIV == "hi")), digits = 3) round(cpquery(fitted_f16_2, event = (Mortality == "yes"), evidence = (LIV == "hi")), digits = 3) |
0.135
0.137
3. bnlearn解析:その3:dealライブラリを用いて、データから学習させてモデル構築
|
1 |
library(deal) |
|
1 2 3 4 5 6 7 |
df1FR <- df1F df1FR$XYZ <- factor(rep("xyz", nrow(df1FR))) df2FR <- df2F df2FR$XYZ <- factor(rep("xyz", nrow(df2FR))) #marks |
|
1 2 3 4 |
net1 = network(df1FR) net2 = network(df2FR) net1 net2 |
## 17 ( 6 discrete+ 11 ) nodes;score= ;relscore=
1 MV discrete(2)
2 ROX discrete(2)
3 LIV discrete(2)
4 Gender discrete(2)
5 Age continuous()
6 BMI continuous()
7 WBC continuous()
8 Cr continuous()
9 CRP continuous()
10 LDH continuous()
11 Ddim continuous()
12 PSI continuous()
13 CCI continuous()
14 DtoH continuous()
15 DtoHF continuous()
16 Mortality discrete(2)
17 XYZ discrete(1)
## 17 ( 6 discrete+ 11 ) nodes;score= ;relscore=
1 MV discrete(2)
2 ROX discrete(2)
3 LIV discrete(2)
4 Gender discrete(2)
5 Age continuous()
6 BMI continuous()
7 WBC continuous()
8 Cr continuous()
9 CRP continuous()
10 LDH continuous()
11 Ddim continuous()
12 PSI continuous()
13 CCI continuous()
14 DtoH continuous()
15 DtoHF continuous()
16 Mortality discrete(2)
17 XYZ discrete(1)
|
1 2 |
prior1 = jointprior(net1, N = 64) prior2 = jointprior(net2, N = 64) |
Imaginary sample size: 64
Imaginary sample size: 64
|
1 2 3 4 5 6 7 8 9 |
net1 = learn(net2, df1FR, prior1)$nw best1 = autosearch(net1, df1FR, prior1) mstring1 = deal::modelstring(best$nw) mstring1 net2 = learn(net2, df2FR, prior2)$nw best2 = autosearch(net2, df1FR, prior2) mstring2 = deal::modelstring(best$nw) mstring2 |
|
1 2 3 4 |
bn.deal1 = model2network(mstring1) bn.deal2 = model2network(mstring2) bn.deal1 bn.deal2 |
Random/Generated Bayesian network
model:
[Mortality][XYZ][Gender|Mortality][LIV|Mortality][DtoHF|Gender:LIV:Mortality]
[MV|LIV:Mortality][ROX|LIV:MV:Mortality][Cr|Gender:LIV:Mortality:ROX]
[Ddim|Gender:LIV:Mortality:ROX][DtoH|DtoHF:Gender:Mortality:ROX]
[CCI|Cr:Gender:ROX][CRP|Cr:Gender:LIV:Mortality]
[LDH|Ddim:Gender:LIV:Mortality:ROX][PSI|CCI:CRP:Cr:LDH:LIV]
[Age|LIV:Mortality:PSI][BMI|Age:LIV:Mortality][WBC|BMI:CRP:ROX]
nodes: 17
arcs: 48
undirected arcs: 0
directed arcs: 48
average markov blanket size: 7.06
average neighbourhood size: 5.65
average branching factor: 2.82
generation algorithm: Empty
Random/Generated Bayesian network
model:
[Mortality][XYZ][Gender|Mortality][LIV|Mortality][DtoHF|Gender:LIV:Mortality]
[MV|LIV:Mortality][ROX|LIV:MV:Mortality][Cr|Gender:LIV:Mortality:ROX]
[Ddim|Gender:LIV:Mortality:ROX][DtoH|DtoHF:Gender:Mortality:ROX]
[CCI|Cr:Gender:ROX][CRP|Cr:Gender:LIV:Mortality]
[LDH|Ddim:Gender:LIV:Mortality:ROX][PSI|CCI:CRP:Cr:LDH:LIV]
[Age|LIV:Mortality:PSI][BMI|Age:LIV:Mortality][WBC|BMI:CRP:ROX]
nodes: 17
arcs: 48
undirected arcs: 0
directed arcs: 48
average markov blanket size: 7.06
average neighbourhood size: 5.65
average branching factor: 2.82
generation algorithm: Empty
|
1 |
graphviz.plot(bn.deal1) |
|
1 |
graphviz.plot(bn.deal2) |
|
1 2 3 4 5 |
res1 = hc(df1FR) bnlearn::modelstring(res1) res2 = hc(df2FR) bnlearn::modelstring(res2) |
‘[MV][Gender][Age][WBC][CRP][XYZ][ROX|MV][LIV|MV][BMI|Age][LDH|MV][DtoH|MV][Mortality|MV][Cr|ROX:Mortality][Ddim|ROX:Gender:Mortality][PSI|Age:CRP:Mortality][DtoHF|DtoH][CCI|ROX:PSI]’
‘[MV][Gender][WBC][CRP][XYZ][ROX|MV][LIV|MV][LDH|MV][DtoH|MV][Mortality|MV][BMI|ROX][Cr|MV:Gender:Mortality][DtoHF|ROX:DtoH][Age|BMI][Ddim|ROX:Gender:BMI:DtoH][PSI|Age:CRP:Mortality][CCI|CRP:PSI]’
|
1 2 |
bnlearn::node.ordering(res1) bnlearn::node.ordering(res2) |
‘MV”Gender”Age”WBC”CRP”XYZ”ROX”LIV”BMI”LDH”DtoH”Mortality”Cr”Ddim”PSI”DtoHF”CCI’
‘MV”Gender”WBC”CRP”XYZ”ROX”LIV”LDH”DtoH”Mortality”BMI”Cr”DtoHF”Age”Ddim”PSI”CCI’
|
1 2 3 4 5 6 7 |
net1 = deal::network(df1FR[, node.ordering(res1)]) net1 = deal::as.network(bnlearn::modelstring(res), net1) deal::modelstring(net1) net2 = deal::network(df2FR[, node.ordering(res2)]) net2 = deal::as.network(bnlearn::modelstring(res2), net2) deal::modelstring(net2) |
‘[MV][Gender][Age][WBC][CRP][XYZ][ROX|MV][LIV|MV][BMI|Age][LDH|MV][DtoH|MV][Mortality|MV][Cr|ROX:Mortality][Ddim|Gender:ROX:Mortality][PSI|Age:CRP:Mortality][DtoHF|DtoH][CCI|ROX:PSI]’
‘[MV][Gender][WBC][CRP][XYZ][ROX|MV][LIV|MV][LDH|MV][DtoH|MV][Mortality|MV][BMI|ROX][Cr|MV:Gender:Mortality][DtoHF|ROX:DtoH][Age|BMI][Ddim|Gender:ROX:DtoH:BMI][PSI|CRP:Mortality:Age][CCI|CRP:PSI]’
|
1 2 |
bnlearn::modelstring(res1) bnlearn::modelstring(res2) |
‘[MV][Gender][Age][WBC][CRP][XYZ][ROX|MV][LIV|MV][BMI|Age][LDH|MV][DtoH|MV][Mortality|MV][Cr|ROX:Mortality][Ddim|ROX:Gender:Mortality][PSI|Age:CRP:Mortality][DtoHF|DtoH][CCI|ROX:PSI]’
‘[MV][Gender][WBC][CRP][XYZ][ROX|MV][LIV|MV][LDH|MV][DtoH|MV][Mortality|MV][BMI|ROX][Cr|MV:Gender:Mortality][DtoHF|ROX:DtoH][Age|BMI][Ddim|ROX:Gender:BMI:DtoH][PSI|Age:CRP:Mortality][CCI|CRP:PSI]’
|
1 2 3 4 5 |
res1R = bnlearn::model2network(deal::modelstring(net1)) res1R res2R = bnlearn::model2network(deal::modelstring(net2)) res2R |
Random/Generated Bayesian network
model:
[Age][CRP][Gender][MV][WBC][XYZ][BMI|Age][DtoH|MV][LDH|MV][LIV|MV]
[Mortality|MV][ROX|MV][Cr|Mortality:ROX][Ddim|Gender:Mortality:ROX]
[DtoHF|DtoH][PSI|Age:CRP:Mortality][CCI|PSI:ROX]
nodes: 17
arcs: 17
undirected arcs: 0
directed arcs: 17
average markov blanket size: 2.82
average neighbourhood size: 2.00
average branching factor: 1.00
generation algorithm: Empty
Random/Generated Bayesian network
model:
[CRP][Gender][MV][WBC][XYZ][DtoH|MV][LDH|MV][LIV|MV][Mortality|MV][ROX|MV]
[BMI|ROX][Cr|Gender:MV:Mortality][DtoHF|DtoH:ROX][Age|BMI]
[Ddim|BMI:DtoH:Gender:ROX][PSI|Age:CRP:Mortality][CCI|CRP:PSI]
nodes: 17
arcs: 21
undirected arcs: 0
directed arcs: 21
average markov blanket size: 3.65
average neighbourhood size: 2.47
average branching factor: 1.24
generation algorithm: Empty
|
1 |
plot(res1R) |
|
1 |
graphviz.plot(res2) |
|
1 |
graphviz.plot(res1) |
|
1 |
plot(res2R) |
|
1 |
graphviz.plot(res2R) |
推測3
|
1 2 |
fitted_f16_1 = bn.fit(res1R, data = df1FR) fitted_f16_2 = bn.fit(res2R, data = df2FR) |
|
1 2 3 4 5 6 7 8 9 10 |
print("P(MV=on, ROX=Low)") round(cpquery(fitted_f16_1, event = (MV == "on"), evidence = (ROX == "lo")), digits = 3) print("P(MV=on, ROX=Low)") round(cpquery(fitted_f16_2, event = (MV == "on"), evidence = (ROX == "lo")), digits = 3) print("P(MV=on, ROX=High)") round(cpquery(fitted_f16_1, event = (MV == "on"), evidence = (ROX == "hi")), digits = 3) print("P(MV=on, ROX=High)") round(cpquery(fitted_f16_2, event = (MV == "on"), evidence = (ROX == "hi")), digits = 3) |
[1] “P(MV=on, ROX=Low)”
0.723
[1] “P(MV=on, ROX=Low)”
0.903
尤度は、ROX<=6.1では人工呼吸率は78.3%、ROX<=4.88では人工呼吸率は90.0%
であったので、ほぼ近い。
[1] “P(MV=on, ROX=High)”
0.171
[1] “P(MV=on, ROX=High)”
0.308
|
1 2 3 4 5 6 7 8 9 |
print("P(Mortality=yes, ROX=Low)") round(cpquery(fitted_f16_1, event = (Mortality == "yes"), evidence = (ROX == "lo")), digits = 3) print("P(Mortality=yes, ROX=Low)") round(cpquery(fitted_f16_2, event = (Mortality == "yes"), evidence = (ROX == "lo")), digits = 3) print("P(Mortality=yes, ROX=High)") round(cpquery(fitted_f16_1, event = (Mortality == "yes"), evidence = (ROX == "hi")), digits = 3) print("P(Mortality=yes, ROX=High)") round(cpquery(fitted_f16_2, event = (Mortality == "yes"), evidence = (ROX == "hi")), digits = 3) |
[1] “P(Mortality=yes, ROX=Low)”
0.124
[1] “P(Mortality=yes, ROX=Low)”
0.139
参考までに尤度は、ROX<=6.1では死亡率は8.0%、ROX<=4.88では人工呼吸率は10.0% であった。
[1] “P(Mortality=yes, ROX=High)”
0.028
[1] “P(Mortality=yes, ROX=High)”
0.049
|
1 2 3 4 5 6 7 8 9 10 |
print("P(MV=on, ROX=Low, LIV=High)") round(cpquery(fitted_f16_1, event = (MV == "on"), evidence = ((ROX == "lo") & (LIV == "hi"))), digits = 3) print("P(MV=on, ROX=Low, LIV=High)") round(cpquery(fitted_f16_2, event = (MV == "on"), evidence = ((ROX == "lo") & (LIV == "hi"))), digits = 3) print("P(MV=off, ROX=Low, LIV=High)") round(cpquery(fitted_f16_1, event = (MV == "off"), evidence = ((ROX == "lo") & (LIV == "hi"))), digits = 3) print("P(MV=off, ROX=Low, LIV=High)") round(cpquery(fitted_f16_2, event = (MV == "off"), evidence = ((ROX == "lo") & (LIV == "hi"))), digits = 3) |
[1] “P(MV=on, ROX=Low, LIV=High)”
0.938
[1] “P(MV=on, ROX=Low, LIV=High)”
0.979
[1] “P(MV=off, ROX=Low, LIV=High)”
0.054
[1] “P(MV=off, ROX=Low, LIV=High)”
0.021
|
1 2 3 4 5 6 7 8 9 |
print("P(MV=ON, ROX=Low, LIV=High, LDH=High)") round(cpquery(fitted_f16_1, event = (MV == "on"), evidence = ((ROX == "lo") & (LIV == "hi") & (LDH > mean(df1F$LDH)))), digits = 3) print("P(MV=ON, ROX=Low, LIV=High, LDH=High)") round(cpquery(fitted_f16_2, event = (MV == "on"), evidence = ((ROX == "lo") & (LIV == "hi") & (LDH > mean(df2F$LDH)))), digits = 3) print("P(MV=OFF, ROX=Low, LIV=High, LDH=High)") round(cpquery(fitted_f16_1, event = (MV == "off"), evidence = ((ROX == "lo") & (LIV == "hi") & (LDH > mean(df1F$LDH)))), digits = 3) print("P(MV=OFF, ROX=Low, LIV=High, LDH=High)") round(cpquery(fitted_f16_2, event = (MV == "off"), evidence = ((ROX == "lo") & (LIV == "hi") & (LDH > mean(df2F$LDH)))), digits = 3) |
[1] “P(MV=ON, ROX=Low, LIV=High, LDH=High)”
0.984
[1] “P(MV=ON, ROX=Low, LIV=High, LDH=High)”
0.997
[1] “P(MV=OFF, ROX=Low, LIV=High, LDH=High)”
0.013
[1] “P(MV=OFF, ROX=Low, LIV=High, LDH=High)”
0.004
|
1 2 3 4 5 6 7 8 9 10 |
print("P(MV=ON, ROX=Low, LIV=High, LDH=High, Age=High)") round(cpquery(fitted_f16_1, event = (MV == "on"), evidence = ((ROX == "lo") & (LIV == "hi") & (LDH > mean(df2F$LDH)) & (Age > mean(df2F$Age)))), digits = 3) print("P(MV=ON, ROX=Low, LIV=High, LDH=High, Age=High)") round(cpquery(fitted_f16_2, event = (MV == "on"), evidence = ((ROX == "lo") & (LIV == "hi") & (LDH > mean(df2F$LDH)) & (Age > mean(df2F$Age)))), digits = 3) print("P(MV=OFF, ROX=Low, LIV=High, LDH=High, Age=High)") round(cpquery(fitted_f16_1, event = (MV == "off"), evidence = ((ROX == "lo") & (LIV == "hi") & (LDH >mean(df1F$LDH)) & (Age> mean(df1F$Age)))), digits = 3) print("P(MV=OFF, ROX=Low, LIV=High, LDH=High, Age=High)") round(cpquery(fitted_f16_2, event = (MV == "off"), evidence = ((ROX == "lo") & (LIV == "hi") & (LDH >mean(df2F$LDH)) & (Age> mean(df2F$Age)))), digits = 3) |
[1] “P(MV=ON, ROX=Low, LIV=High, LDH=High, Age=High)”
0.984
[1] “P(MV=ON, ROX=Low, LIV=High, LDH=High, Age=High)”
0.984
[1] “P(MV=OFF, ROX=Low, LIV=High, LDH=High, Age=High)”
0.018
[1] “P(MV=OFF, ROX=Low, LIV=High, LDH=High, Age=High)”
0.007
4. bnlearn解析:その4:すべてをカテゴリカルデータに変換して、Hill-Climb法
|
1 2 3 4 |
library("infotheo") df_f1_dc <- infotheo::discretize(df1F, disc="equalwidth", nbins=2) df_f2_dc <- infotheo::discretize(df2F, disc="equalwidth", nbins=2) |
|
1 |
df_f1_dc |
A data.frame: 59 × 16
MV ROX LIV Gender Age BMI WBC Cr CRP LDH Ddim PSI CCI DtoH DtoHF Mortality
1 2 1 1 1 2 2 2 2 1 1 1 1 1 1 1
1 2 1 2 2 2 1 1 2 2 2 2 2 1 1 1
1 2 1 2 1 2 2 1 2 1 2 1 1 1 1 1
1 2 1 2 2 1 2 1 1 1 1 1 1 2 2 1
………..
|
1 |
df_f2_dc |
A data.frame: 59 × 16
MV ROX LIV Gender Age BMI WBC Cr CRP LDH Ddim PSI CCI DtoH DtoHF Mortality
1 2 1 1 1 2 2 2 2 1 1 1 1 1 1 1
1 2 1 2 2 2 1 1 2 2 2 2 2 1 1 1
1 2 1 2 1 2 2 1 2 1 2 1 1 1 1 1
1 2 1 2 2 1 2 1 1 1 1 1 1 2 2 1
1 2 1 1 1 2 2 1 2 2 2 1 1 2 2 1
……………
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
df_f1_dc <- df_f1_dc %>% mutate(MV = factor(MV, levels = c(1, 2))) df_f1_dc <- df_f1_dc %>% mutate(ROX = factor(ROX, levels = c(1, 2))) df_f1_dc <- df_f1_dc %>% mutate(LIV = factor(LIV, levels = c(1, 2))) df_f1_dc <- df_f1_dc %>% mutate(Gender = factor(Gender, levels = c(1, 2))) df_f1_dc <- df_f1_dc %>% mutate(Age = factor(Age, levels = c(1, 2))) df_f1_dc <- df_f1_dc %>% mutate(BMI = factor(BMI, levels = c(1, 2))) df_f1_dc <- df_f1_dc %>% mutate(WBC = factor(WBC, levels = c(1, 2))) df_f1_dc <- df_f1_dc %>% mutate(Cr = factor(Cr, levels = c(1, 2))) df_f1_dc <- df_f1_dc %>% mutate(CRP = factor(CRP, levels = c(1, 2))) df_f1_dc <- df_f1_dc %>% mutate(LDH = factor(LDH, levels = c(1, 2))) df_f1_dc <- df_f1_dc %>% mutate(Ddim = factor(Ddim, levels = c(1, 2))) df_f1_dc <- df_f1_dc %>% mutate(PSI = factor(PSI, levels = c(1, 2))) df_f1_dc <- df_f1_dc %>% mutate(CCI = factor(CCI, levels = c(1, 2))) df_f1_dc <- df_f1_dc %>% mutate(DtoH = factor(DtoH, levels = c(1, 2))) df_f1_dc <- df_f1_dc %>% mutate(DtoHF = factor(DtoHF, levels = c(1, 2))) df_f1_dc <- df_f1_dc %>% mutate(Mortality = factor(Mortality, levels = c(1, 2))) |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
df_f2_dc <- df_f2_dc %>% mutate(MV = factor(MV, levels = c(1, 2))) df_f2_dc <- df_f2_dc %>% mutate(ROX = factor(ROX, levels = c(1, 2))) df_f2_dc <- df_f2_dc %>% mutate(LIV = factor(LIV, levels = c(1, 2))) df_f2_dc <- df_f2_dc %>% mutate(Gender = factor(Gender, levels = c(1, 2))) df_f2_dc <- df_f2_dc %>% mutate(Age = factor(Age, levels = c(1, 2))) df_f2_dc <- df_f2_dc %>% mutate(BMI = factor(BMI, levels = c(1, 2))) df_f2_dc <- df_f2_dc %>% mutate(WBC = factor(WBC, levels = c(1, 2))) df_f2_dc <- df_f2_dc %>% mutate(Cr = factor(Cr, levels = c(1, 2))) df_f2_dc <- df_f2_dc %>% mutate(CRP = factor(CRP, levels = c(1, 2))) df_f2_dc <- df_f2_dc %>% mutate(LDH = factor(LDH, levels = c(1, 2))) df_f2_dc <- df_f2_dc %>% mutate(Ddim = factor(Ddim, levels = c(1, 2))) df_f2_dc <- df_f2_dc %>% mutate(PSI = factor(PSI, levels = c(1, 2))) df_f2_dc <- df_f2_dc %>% mutate(CCI = factor(CCI, levels = c(1, 2))) df_f2_dc <- df_f2_dc %>% mutate(DtoH = factor(DtoH, levels = c(1, 2))) df_f2_dc <- df_f2_dc %>% mutate(DtoHF = factor(DtoHF, levels = c(1, 2))) df_f2_dc <- df_f2_dc %>% mutate(Mortality = factor(Mortality, levels = c(1, 2))) |
|
1 |
df_f1_dc |
A data.frame: 59 × 16
MV ROX LIV Gender Age BMI WBC Cr CRP LDH Ddim PSI CCI DtoH DtoHF Mortality
1 2 1 1 1 2 2 2 2 1 1 1 1 1 1 1
1 2 1 2 2 2 1 1 2 2 2 2 2 1 1 1
1 2 1 2 1 2 2 1 2 1 2 1 1 1 1 1
1 2 1 2 2 1 2 1 1 1 1 1 1 2 2 1
1 1 1 1 1 2 2 1 2 2 2 1 1 2 2 1
……………
|
1 |
df_f1_dc |
A data.frame: 59 × 16
MV ROX LIV Gender Age BMI WBC Cr CRP LDH Ddim PSI CCI DtoH DtoHF Mortality
1 1 2 1 1 2 1 1 1 1 1 1 1 1 1 1
1 1 2 2 2 1 1 1 1 1 1 1 1 1 1 1
1 1 2 2 1 1 1 1 1 1 1 1 1 1 1 1
1 1 2 2 2 1 2 1 1 1 1 1 1 2 2 1
1 1 2 1 1 1 1 1 1 1 2 1 1 2 2 1
……………
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
#もともとのカテゴリカルデータを、元のカテゴリーにマッチするように戻す。 df_f1_dc$MV[df1$MV == "off"] <- 1 df_f1_dc$MV[df1$MV == "on"] <- 2 df_f1_dc$ROX[df1$ROX == "lo"] <- 1 df_f1_dc$ROX[df1$ROX == "hi"] <- 2 df_f1_dc$LIV[df1$LIV == "lo"] <- 1 df_f1_dc$LIV[df1$LIV == "hi"] <- 2 df_f1_dc$Gender[df1$Gender == "female"] <- 1 df_f1_dc$Gender[df1$Gender == "male"] <- 2 df_f1_dc$Mortality[df1$Mortality == "no"] <- 1 df_f1_dc$Mortality[df1$Mortality == "yes"] <- 2 df_f1_dc df_f2_dc$MV[df2$MV == "off"] <- 1 df_f2_dc$MV[df2$MV == "on"] <- 2 df_f2_dc$ROX[df2$ROX == "lo"] <- 1 df_f2_dc$ROX[df2$ROX == "hi"] <- 2 df_f2_dc$LIV[df2$LIV == "lo"] <- 1 df_f2_dc$LIV[df2$LIV == "hi"] <- 2 df_f2_dc$Gender[df2$Gender == "female"] <- 1 df_f2_dc$Gender[df2$Gender == "male"] <- 2 df_f2_dc$Mortality[df2$Mortality == "no"] <- 1 df_f2_dc$Mortality[df2$Mortality == "yes"] <- 2 df_f2_dc |
|
1 2 3 4 5 |
dag1_dc = hc(df_f1_dc, whitelist = wl2, blacklist = bl2) dag2_dc = hc(df_f2_dc, whitelist = wl2, blacklist = bl2) dag1_dc dag2_dc |
Bayesian network learned via Score-based methods
model:
[Gender][Cr][CRP][Ddim][CCI|Cr][ROX|CCI][Age|CCI][LIV|ROX][BMI|Age][WBC|ROX]
[PSI|Age][MV|ROX:LIV][LDH|MV:LIV][DtoH|MV][Mortality|MV:ROX:LIV][DtoHF|DtoH]
nodes: 16
arcs: 16
undirected arcs: 0
directed arcs: 16
average markov blanket size: 2.00
average neighbourhood size: 2.00
average branching factor: 1.00
learning algorithm: Hill-Climbing
score: BIC (disc.)
penalization coefficient: 2.038769
tests used in the learning procedure: 292
optimized: TRUE
Bayesian network learned via Score-based methods
model:
[ROX][Gender][WBC][Cr][CRP][Ddim][LIV|ROX][CCI|Cr][MV|ROX:LIV][Age|CCI]
[BMI|Age][LDH|MV:LIV][PSI|Age][DtoH|MV][Mortality|MV:ROX:LIV][DtoHF|DtoH]
nodes: 16
arcs: 14
undirected arcs: 0
directed arcs: 14
average markov blanket size: 1.75
average neighbourhood size: 1.75
average branching factor: 0.88
learning algorithm: Hill-Climbing
score: BIC (disc.)
penalization coefficient: 2.038769
tests used in the learning procedure: 264
optimized: TRUE
|
1 |
graphviz.plot(dag1_dc, shape = "ellipse", highlight = list(arcs = wl2)) |
|
1 |
graphviz.plot(dag2_dc, shape = "ellipse", highlight = list(arcs = wl2)) |
|
1 2 |
par(mfrow = c(1,2)) graphviz.compare(dag1_dc, dag2_dc, shape = "ellipse", main = c("DAG ROX6.1", "DAG ROX4.88")) |
推測4
|
1 2 3 4 |
fitted.simpler_dc_1 = bn.fit(dag1_dc, data = df_f1_dc) fitted.simpler_dc_2 = bn.fit(dag2_dc, data = df_f2_dc) fitted.simpler_dc_1 fitted.simpler_dc_2 |
|
1 2 3 4 5 6 7 8 9 10 |
print("P(MV=on, ROX=Low)") round(cpquery(fitted.simpler_dc_1, event = (MV == 2), evidence = (ROX == 1)), digits = 3) print("P(MV=on, ROX=Low)") round(cpquery(fitted.simpler_dc_1, event = (MV == 2), evidence = (ROX == 1)), digits = 3) print("P(MV=on, ROX=High)") round(cpquery(fitted.simpler_dc_2, event = (MV == 2), evidence = (ROX == 2)), digits = 3) print("P(MV=on, ROX=High)") round(cpquery(fitted.simpler_dc_2, event = (MV == 2), evidence = (ROX == 2)), digits = 3) |
[1] “P(MV=on, ROX=Low)”
0.723
[1] “P(MV=on, ROX=Low)”
0.715
[1] “P(MV=on, ROX=High)”
0.306
[1] “P(MV=on, ROX=High)”
0.309
|
1 2 3 4 5 6 7 8 9 |
print("P(Mortality=yes, ROX=Low)") round(cpquery(fitted.simpler_dc_1, event = (Mortality == 2), evidence = (ROX == 1)), digits = 3) print("P(Mortality=yes, ROX=Low)") round(cpquery(fitted.simpler_dc_1, event = (Mortality == 2), evidence = (ROX == 1)), digits = 3) print("P(Mortality=yes, ROX=High)") round(cpquery(fitted.simpler_dc_2, event = (Mortality == 2), evidence = (ROX == 2)), digits = 3) print("P(Mortality=yes, ROX=High)") round(cpquery(fitted.simpler_dc_2, event = (Mortality == 2), evidence = (ROX == 2)), digits = 3) |
[1] “P(Mortality=yes, ROX=Low)”
0.079
[1] “P(Mortality=yes, ROX=Low)”
0.078
[1] “P(Mortality=yes, ROX=High)”
0.063
[1] “P(Mortality=yes, ROX=High)”
0.065
|
1 2 3 4 5 6 7 8 9 10 |
print("P(MV=on, ROX=Low, LIV=High)") round(cpquery(fitted.simpler_dc_1, event = (MV == 2), evidence = ((ROX == 1) & (LIV == 2))), digits = 3) print("P(MV=on, ROX=Low, LIV=High)") round(cpquery(fitted.simpler_dc_1, event = (MV == 2), evidence = ((ROX == 1) & (LIV == 2))), digits = 3) print("P(MV=off, ROX=Low, LIV=High)") round(cpquery(fitted.simpler_dc_2, event = (MV == 1), evidence = ((ROX == 1) & (LIV == 2))), digits = 3) print("P(MV=off, ROX=Low, LIV=High)") round(cpquery(fitted.simpler_dc_2, event = (MV == 1), evidence = ((ROX == 1) & (LIV == 2))), digits = 3) |
[1] “P(MV=on, ROX=Low, LIV=High)”
0.931
[1] “P(MV=on, ROX=Low, LIV=High)”
0.928
[1] “P(MV=off, ROX=Low, LIV=High)”
0
[1] “P(MV=off, ROX=Low, LIV=High)”
0
5. bnlearn解析:その55:カテゴリカルデータを用いて、ブートストラップ法
|
1 2 |
str.raw1.dc = boot.strength(df_f1_dc, R = 200, algorithm = "hc", algorithm.args = list(whitelist = wl2, blacklist = bl2)) attr(str.raw1.dc, "threshold") |
0.48
|
1 2 |
str.raw2.dc = boot.strength(df_f2_dc, R = 200, algorithm = "hc", algorithm.args = list(whitelist = wl2, blacklist = bl2)) attr(str.raw2.dc, "threshold") |
0.495
|
1 2 |
avg.df1_dc = averaged.network(str.raw1.dc) strength.plot(avg.df1_dc, str.raw1.dc, shape = "ellipse", highlight = list(arcs = wl2)) |
|
1 2 |
avg.df2_dc = averaged.network(str.raw2.dc) strength.plot(avg.df2_dc, str.raw2.dc, shape = "ellipse", highlight = list(arcs = wl2)) |
|
1 2 |
par(mfrow = c(1,2)) graphviz.compare(avg.df1_dc, avg.df2_dc, shape = "ellipse", main = c("DAG ROX6.1", "DAG ROX4.88")) |
|
1 2 |
avg.raw.full1_dc = averaged.network(str.raw1.dc) avg.raw.full2_dc = averaged.network(str.raw2.dc) |
|
1 |
strength.plot(avg.raw.full1_dc, str.raw1.dc, shape = "ellipse", highlight = list(arcs = wl2)) |
|
1 |
strength.plot(avg.raw.full2_dc, str.raw2.dc, shape = "ellipse", highlight = list(arcs = wl2)) |
|
1 2 |
par(mfrow = c(1,2)) graphviz.compare(avg.raw.full1_dc, avg.raw.full2_dc, shape = "ellipse", main = c("DAG ROX6.1", "DAG ROX4.88")) |
推測5
|
1 2 |
fitted_f16_1_dc = bn.fit(avg.raw.full1_dc, data = df_f1_dc) fitted_f16_2_dc = bn.fit(avg.raw.full2_dc, data = df_f2_dc) |
|
1 2 3 |
# MV:on, ROX:low round(cpquery(fitted_f16_1_dc, event = (MV == 2), evidence = (ROX == 1)), digits = 3) round(cpquery(fitted_f16_2_dc, event = (MV == 2), evidence = (ROX == 1)), digits = 3) |
0.723
0.893
尤度は、ROX<=6.1では人工呼吸率は78.3%、ROX<=4.88では人工呼吸率は90.0% であったので、ほぼ近い。
|
1 2 3 |
# MV:on, ROX:hi round(cpquery(fitted_f16_1_dc, event = (MV == 2), evidence = (ROX == 2)), digits = 3) round(cpquery(fitted_f16_2_dc, event = (MV == 2), evidence = (ROX == 2)), digits = 3) |
0.178
0.307
|
1 2 3 |
# MV:OFF, ROX:hi round(cpquery(fitted_f16_1_dc, event = (MV == 1), evidence = (ROX == 2)), digits = 3) round(cpquery(fitted_f16_2_dc, event = (MV == 1), evidence = (ROX == 2)), digits = 3) |
0.828
0.692
|
1 2 3 |
# MV:OFF, ROX:low round(cpquery(fitted_f16_1_dc, event = (MV == 1), evidence = (ROX == 1)), digits = 3) round(cpquery(fitted_f16_2_dc, event = (MV == 1), evidence = (ROX == 1)), digits = 3) |
0.292
0.1
|
1 2 3 |
# Mortality:yes, MV:on round(cpquery(fitted_f16_1_dc, event = (Mortality == 2), evidence = (MV == 2)), digits = 3) round(cpquery(fitted_f16_2_dc, event = (Mortality == 2), evidence = (MV == 2)), digits = 3) |
0.17
0.167
|
1 2 3 |
# Mortality:yes, ROX:low round(cpquery(fitted_f16_1_dc, event = (Mortality == 2), evidence = (ROX == 1)), digits = 3) round(cpquery(fitted_f16_2_dc, event = (Mortality == 2), evidence = (ROX == 1)), digits = 3) |
0.088
0.086
参考までに尤度は、ROX<=6.1では死亡率は8.0%、ROX<=4.88では人工呼吸率は10.0% であった。
|
1 2 3 |
# Mortality:yes, LIV:hi round(cpquery(fitted_f16_1_dc, event = (Mortality == 2), evidence = (LIV == 2)), digits = 3) round(cpquery(fitted_f16_2_dc, event = (Mortality == 2), evidence = (LIV == 2)), digits = 3) |
0.139
0.136