????????????
ベイズ推論による機械学習入門 須山 敦志 著 を読む
????????????
Polynomial Regression
????????????
導入する自作モジュール無しで、demo_PolynomialRegression.jlをどんどん入力実行へ:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
################################# ## Bayesian model selection demo ## for polynomial regression using PyPlot, PyCall using Distributions function poly(X_raw, M) N = size(X_raw, 1) X = zeros(M, N) for m in 0 : M - 1 X[m+1,:] = X_raw.^m end return X end |
Out: poly (generic function with 1 method)
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
function learn_bayes(X_raw, Y, M, sig2_y, Sig_w, X_lin) X = poly(X_raw, M) N = size(X_raw, 1) # calc posterior Sig_w_h = inv(X*inv(sig2_y*eye(N))*X' + inv(Sig_w)) mu_w_h = Sig_w_h * (X * inv(sig2_y * eye(N)) * Y) # calc predictive X_test = poly(X_lin, M) Y_est = (mu_w_h'*X_test)' sig2_y_prd = sig2_y + diag(X_test'Sig_w_h*X_test) # calc evidence evidence = -0.5*(sum(Y)*inv(sig2_y) +N*log.(sig2_y) + N*log.(2*pi) + logdet(Sig_w) - (mu_w_h'*inv(Sig_w_h)*mu_w_h)[1] - logdet(Sig_w_h) ) return Y_est, sqrt.(sig2_y_prd), evidence end |
Out: learn_bayes (generic function with 1 method)
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 |
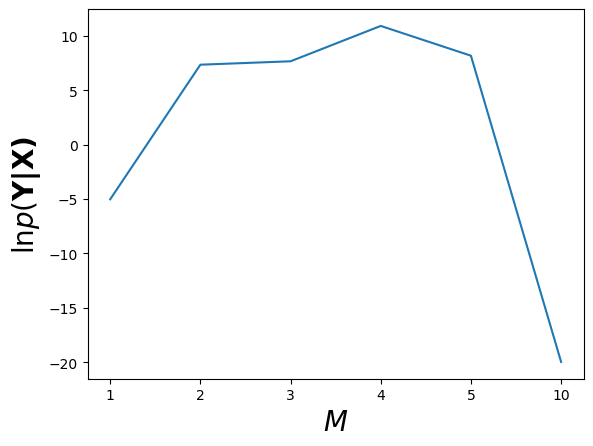
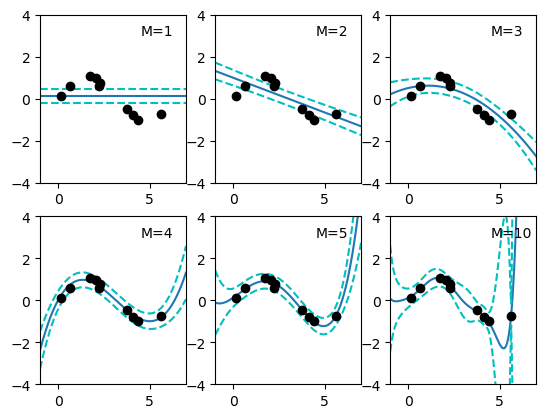
function test() # linspace X_lin = linspace(-1, 7, 200) # generate data N = 10 sig2_y = 0.1 X = 2*pi*rand(N) Y_true = [sin.(x) for x in X_lin] Y_obs = [sin.(x) + sig2_y * randn() for x in X] dims = [1, 2, 3, 4, 5, 10] # learning via Bayes sig2_w = 1.0 Y_bayes = [learn_bayes(X, Y_obs, m, sig2_y, sig2_w*eye(m), X_lin) for m in dims] ############# # compute evidences evidence = [learn_bayes(X, Y_obs, m, sig2_y, sig2_w*eye(m), X_lin)[3] for m in dims] figure("evidence") clf() plot(1:length(dims), evidence) xticks(1:length(dims),dims) ylabel(("\$\\ln p(\\bf{Y}|\\bf{X})\$"), fontsize=20) xlabel(("\$M\$"), fontsize=20) ############# # visualize x_min = X_lin[1] x_max = X_lin[end] y_min = -4 y_max = 4 figure("prediction") clf() for k in 1 : 6 subplot(230 + k) plot(X_lin, Y_bayes[k][1]) plot(X_lin, Y_bayes[k][1] + Y_bayes[k][2], "c--") plot(X_lin, Y_bayes[k][1] - Y_bayes[k][2], "c--") plot(X, Y_obs, "ko") xlim([x_min, x_max]) ylim([y_min, y_max]) text(x_max - 2.5, y_max - 1, @sprintf("M=%d", dims[k])) end show() end |
Out: test (generic function with 1 method)