Julia #1: LogisticRegression – Science To Medicine

Julia を導入
————————————
ベイズ推論による機械学習入門　須山敦志　著　を読む
————————————
内容としては、機械学習とベイズ推論の基礎を復習するのに良かった。
あとは、本書籍のサポートサイト、著者のサポートサイトを参考に進めるが、サンプルプログラムはJuliaで記述されている。というわけで、Juliaで対応してみる。以前にも経験済だが、最新のver1.2では、色々と仕様が変更されており、書籍の執筆された時点での環境との不一致か、なかなか安定した動作が期待できないのと、貼付のDockerファイルもMacではハングして達成できない。仕方無しにJulia ver 0.7にダウングレードしてみた。

https://julialang.org/からMac OX S用をダウンロードすればよいが、現時点での最新版は1.2だが、ver 0.4, 0.7から相当に改変があり、ここでは、学習プログラムを動かすためにあえて、Older Releasesからver0.7をダウンロードしてインストールする。

(注：あとから気がついたが、ver 0.6.4にして、そのままコードをjupyterに落とせば、何の問題もなく作動！）

以下のパスを.bashrc に追記

export PATH=${PATH}:/Applications/Julia-0.7.app/Contents/Resources/julia/bin

1	export PATH=${PATH}:/Applications/Julia-0.7.app/Contents/Resources/julia/bin

$ source .bashrc

以下のエリアスは、.bash_profileに追記

echo "alias julia='/Applications/Julia-0.7.app/Contents/Resources/julia/bin/julia'

1	echo "alias julia='/Applications/Julia-0.7.app/Contents/Resources/julia/bin/julia'

$ source .bash_profile

Jupyter Notebookでの使用は、Juliaを立ち上げ、

using Pkg
Pkg.add("IJulia")
Pkg.build("IJulia")

using IJulia
IJulia.notebook()

using Pkg

Pkg.add("IJulia")

Pkg.build("IJulia")

using IJulia

IJulia.notebook()

Pkg.add("PyPlot")
Pkg.build("PyPlot")

Pkg.add("PyCall")
Pkg.build("PyCall")

Pkg.add(Distributions")
Pkg.build("Distributions")

Pkg.add("PyPlot")

Pkg.build("PyPlot")

Pkg.add("PyCall")

Pkg.build("PyCall")

Pkg.add(Distributions")

Pkg.build("Distributions")

using PyPlot, PyCall
using Distributions

1 2	using PyPlot, PyCall using Distributions

# true param
W = Array([1.0, 0.0, 1.0])

# generate data
sigma = 0.5
N = 20
X = linspace(-0.4,2.4,N)
Y = [W[1] + W[2]*x + W[3]*x^2 + sigma*randn() for x in X]
X_min = minimum(X)
X_max = maximum(X)

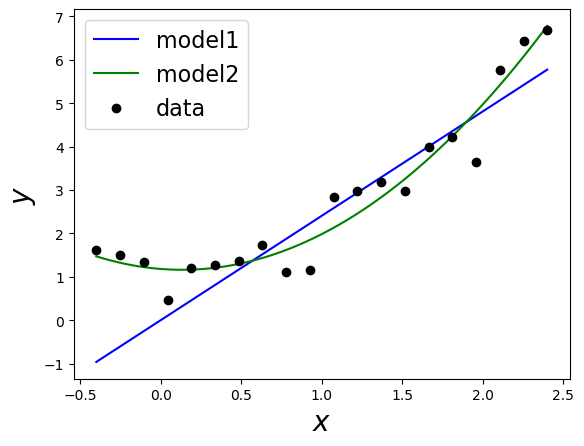
# true param

W = Array([1.0, 0.0, 1.0])

# generate data

sigma = 0.5

N = 20

X = linspace(-0.4,2.4,N)

Y = [W[1] + W[2]*x + W[3]*x^2 + sigma*randn() for x in X]

X_min = minimum(X)

X_max = maximum(X)

Out:2.4

# regression1
X_all = linspace(X_min, X_max, 100)
W1 = sum(Y.*X) / sum(X.^2)
Y1 = [W1*x for x in X_all]

# regression1

X_all = linspace(X_min, X_max, 100)

W1 = sum(Y.*X) / sum(X.^2)

Y1 = [W1*x for x in X_all]

Out: 100-element Array{Float64,1}:
-0.9624213660385834
-0.8943713704600977
-0.826321374881612
-0.7582713793031263
-0.6902213837246407
-0.6221713881461549
-0.5541213925676692
-0.48607139698918356
-0.4180214014106979
-0.34997140583221215
-0.28192141025372647
-0.21387141467524076
-0.14582141909675506
?
5.025978244868158
5.094028240446643
5.162078236025129
5.230128231603614
5.298178227182101
5.366228222760586
5.434278218339072
5.502328213917558
5.570378209496043
5.638428205074529
5.706478200653015
5.7745281962315005

# regression2
X2 = zeros(3, N)
X2[1,:] = 1
X2[2,:] = X
X2[3,:] = X.^2
W2 = inv(X2*X2') * X2*Y
Y2 = [W2[1] + W2[2]*x + W2[3]*x^2 for x in X_all]

# regression2

X2 = zeros(3, N)

X2[1,:] = 1

X2[2,:] = X

X2[3,:] = X.^2

W2 = inv(X2*X2') * X2*Y

Y2 = [W2[1] + W2[2]*x + W2[3]*x^2 for x in X_all]

Out:100-element Array{Float64,1}:
1.4716160624130428
1.4395658262082924
1.4092644768125695
1.3807120142258738
1.3539084384482056
1.3288537494795643
1.3055479473199505
1.2839910319693637
1.2641830034278045
1.2461238616952723
1.2298136067717678
1.2152522386572902
1.2024397573518402
?
5.345933981351435
5.467785784341084
5.591386474139762
5.716736050747467
5.8438345141641985
5.972681864389958
6.103278101424744
6.235623225268559
6.3697172359213985
6.505560133383267
6.643151917654164
6.782492588734086

# show data
figure()
plot(X_all, Y1, "b-")
plot(X_all, Y2, "g-")
plot(X, Y, "ko")
legend(["model1","model2","data"], loc="upper left", fontsize=16)
xlabel("\$x\$", fontsize=20)
ylabel("\$y\$", fontsize=20)
show()

# show data

figure()

plot(X_all, Y1, "b-")

plot(X_all, Y2, "g-")

plot(X, Y, "ko")

legend(["model1","model2","data"], loc="upper left", fontsize=16)

xlabel("\$x\$", fontsize=20)

ylabel("\$y\$", fontsize=20)

show()

次にパッケージLoisticRegressionを追加
Juliaを起動し、]を押してパッケージモードにしてから、

generate LoisticRegression

1	generate LoisticRegression

LogisticRegressionフォルダのsrcの中のLogisticRegression.jlを、ダウンロード済のLogisticRegression.jlに入れ替える。
一度Juliaを終了し、LogisticRegressionディレクトリに入ります。
Juliaを起動して]を押してパッケージモードにして、パッケージの中で利用するパッケージ、ここではDistributionsを以下のようにしてManifest.tomlに登録。

activate .
add Distributions

1 2	activate . add Distributions

delキーを押してパッケージモードを終了した後、

using LogisticRegression

1	using LogisticRegression

ジュピターを立ち上げて、環境OKなる。

notebook(detached=true)

1	notebook(detached=true)

LogisticRegressionのファルダの置かれているPathに要注意して、

using PyPlot, PyCall
using Distributions

push!(LOAD_PATH, "/Users/*****/Desktop/BayesBook-master/src/LogisticRegression")
import LogisticRegression
<pre>
function visualize_surface(mu, rho, X, Y, text)
    N = 100
    R = 100
    xmin = minimum(X[1,:])
    xmax = maximum(X[1,:])
    ymin = minimum(X[2,:])
    ymax = maximum(X[2,:])
    lx = xmax - xmin
    ly = ymax - ymin
    xmin = xmin - 0.25 * lx
    xmax = xmax + 0.25 * lx
    ymin = ymin - 0.25 * ly
    ymax = ymax + 0.25 * ly
    
    x1 = linspace(xmin,xmax,R)
    x2 = linspace(ymin,ymax,R)
    x1grid = repmat(x1, 1, R)
    x2grid = repmat(x2', R, 1)
    val = [x1grid[:] x2grid[:]]'

    z_list = []
    sigma = log.(1 + exp.(rho))
    for n in 1 : N
        W = rand(MvNormal(mu, diagm(sigma.^2)))
        z_tmp = [LogisticRegression.sigmoid(W'*val[:,i]) for i in 1 : size(val, 2)]
        push!(z_list, z_tmp)
    end
    z = mean(z_list)
    zgrid = reshape(z, R, R)

    # 3D plot
    figure("surface")
    clf()
    plot_surface(x1grid, x2grid, zgrid, alpha=0.5)
    scatter3D(X[1,Y.==1], X[2,Y.==1], Y[Y.==1]+0.01, c="r", depthshade=true)
    scatter3D(X[1,Y.==0], X[2,Y.==0], Y[Y.==0], c="b", depthshade=true)
    xlim([xmin, xmax])
    ylim([ymin, ymax])
    zlim([0, 1])
    title(text)
end

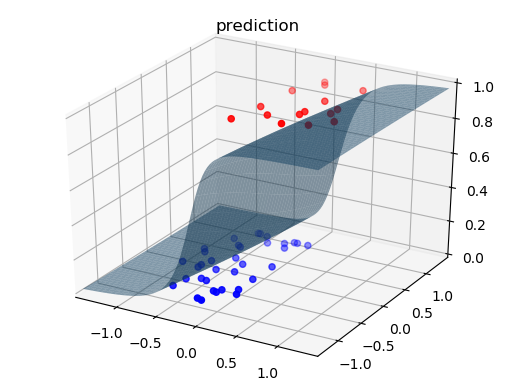
using PyPlot, PyCall

using Distributions

push!(LOAD_PATH, "/Users/*****/Desktop/BayesBook-master/src/LogisticRegression")

import LogisticRegression

<pre>

function visualize_surface(mu, rho, X, Y, text)

N = 100

R = 100

xmin = minimum(X[1,:])

xmax = maximum(X[1,:])

ymin = minimum(X[2,:])

ymax = maximum(X[2,:])

lx = xmax - xmin

ly = ymax - ymin

xmin = xmin - 0.25 * lx

xmax = xmax + 0.25 * lx

ymin = ymin - 0.25 * ly

ymax = ymax + 0.25 * ly

x1 = linspace(xmin,xmax,R)

x2 = linspace(ymin,ymax,R)

x1grid = repmat(x1, 1, R)

x2grid = repmat(x2', R, 1)

val = [x1grid[:] x2grid[:]]'

z_list = []

sigma = log.(1 + exp.(rho))

for n in 1 : N

W = rand(MvNormal(mu, diagm(sigma.^2)))

z_tmp = [LogisticRegression.sigmoid(W'*val[:,i]) for i in 1 : size(val, 2)]

push!(z_list, z_tmp)

end

z = mean(z_list)

zgrid = reshape(z, R, R)

# 3D plot

figure("surface")

clf()

plot_surface(x1grid, x2grid, zgrid, alpha=0.5)

scatter3D(X[1,Y.==1], X[2,Y.==1], Y[Y.==1]+0.01, c="r", depthshade=true)

scatter3D(X[1,Y.==0], X[2,Y.==0], Y[Y.==0], c="b", depthshade=true)

xlim([xmin, xmax])

ylim([ymin, ymax])

zlim([0, 1])

title(text)

end

Out:visualize_surface (generic function with 1 method)

function visualize_contour(mu, rho, X, Y)
    N = 100
    R = 100
    xmin = 2*minimum(X[1,:])
    xmax = 2*maximum(X[1,:])
    ymin = minimum(X[2,:])
    ymax = maximum(X[2,:])

    x1 = linspace(xmin,xmax,R)
    x2 = linspace(ymin,ymax,R)
    x1grid = repmat(x1, 1, R)
    x2grid = repmat(x2', R, 1)
    val = [x1grid[:] x2grid[:]]'

    z_list = []
    W_list = []
    sigma = log.(1 + exp.(rho))
    for n in 1 : N
        W = rand(MvNormal(mu, diagm(sigma.^2)))
        z_tmp = [LogisticRegression.sigmoid(W'*val[:,i]) for i in 1 : size(val, 2)]
        push!(W_list, W)
        push!(z_list, z_tmp)
    end
    z = mean(z_list)
    zgrid = reshape(z, R, R)

    # precition
    figure("contour")
    clf()
    contour(x1grid, x2grid, zgrid, alpha=0.5, cmap=get_cmap("bwr"))
    scatter(X[1,Y.==1], X[2,Y.==1], c="r")
    scatter(X[1,Y.==0], X[2,Y.==0], c="b")
    xlim([xmin, xmax])
    ylim([ymin, ymax])
    title("prediction")

    # parameter samples
    figure("samples")
    clf()
    for n in 1 : 10
        draw_line(W_list[n], xmin, xmax)
    end
    scatter(X[1,Y.==1]', X[2,Y.==1]', c="r")
    scatter(X[1,Y.==0]', X[2,Y.==0]', c="b")
    xlim([xmin, xmax])
    ylim([ymin, ymax])
    title("parameter samples")
end

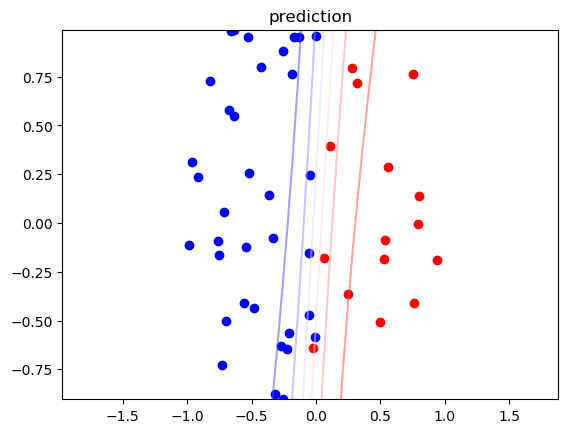
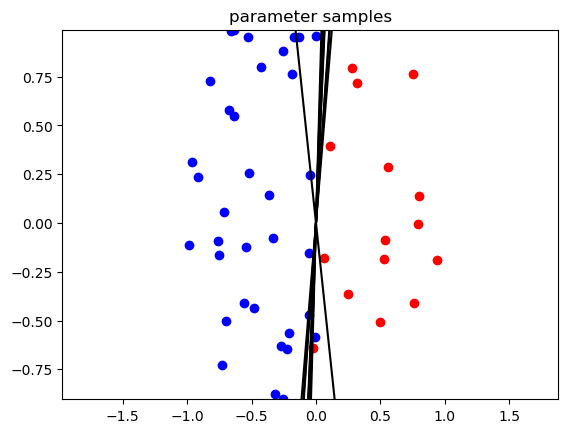
function visualize_contour(mu, rho, X, Y)

N = 100

R = 100

xmin = 2*minimum(X[1,:])

xmax = 2*maximum(X[1,:])

ymin = minimum(X[2,:])

ymax = maximum(X[2,:])

x1 = linspace(xmin,xmax,R)

x2 = linspace(ymin,ymax,R)

x1grid = repmat(x1, 1, R)

x2grid = repmat(x2', R, 1)

val = [x1grid[:] x2grid[:]]'

z_list = []

W_list = []

sigma = log.(1 + exp.(rho))

for n in 1 : N

W = rand(MvNormal(mu, diagm(sigma.^2)))

z_tmp = [LogisticRegression.sigmoid(W'*val[:,i]) for i in 1 : size(val, 2)]

push!(W_list, W)

push!(z_list, z_tmp)

end

z = mean(z_list)

zgrid = reshape(z, R, R)

# precition

figure("contour")

clf()

contour(x1grid, x2grid, zgrid, alpha=0.5, cmap=get_cmap("bwr"))

scatter(X[1,Y.==1], X[2,Y.==1], c="r")

scatter(X[1,Y.==0], X[2,Y.==0], c="b")

xlim([xmin, xmax])

ylim([ymin, ymax])

title("prediction")

# parameter samples

figure("samples")

clf()

for n in 1 : 10

draw_line(W_list[n], xmin, xmax)

end

scatter(X[1,Y.==1]', X[2,Y.==1]', c="r")

scatter(X[1,Y.==0]', X[2,Y.==0]', c="b")

xlim([xmin, xmax])

ylim([ymin, ymax])

title("parameter samples")

end

Out:visualize_contour (generic function with 1 method)

function draw_line(W, xmin, xmax)
    y1 = - xmin*W[1]/W[2]
    y2 = - xmax*W[1]/W[2]
    plot([xmin, xmax], [y1, y2], c="k")
end

function draw_line(W, xmin, xmax)

y1 = - xmin*W[1]/W[2]

y2 = - xmax*W[1]/W[2]

plot([xmin, xmax], [y1, y2], c="k")

end

Out:draw_line (generic function with 1 method)

########################
# create model

M = 2 # input dimension
Sigma_w = 100.0 * eye(M) # prior on W

########################

# create model

M = 2 # input dimension

Sigma_w = 100.0 * eye(M) # prior on W

Out:2×2 Array{Float64,2}:
100.0 0.0
0.0 100.0

########################
# create toy-data using prior model

N = 50 # num of data points
X = 2 * rand(M, N) - 1.0 # input values

# sample observation Y
Y, _ = LogisticRegression.sample_data(X, Sigma_w)

########################

# create toy-data using prior model

N = 50 # num of data points

X = 2 * rand(M, N) - 1.0 # input values

# sample observation Y

Y, _ = LogisticRegression.sample_data(X, Sigma_w)

Out:(Bool[true, false, false, false, false, true, false, false, false, false … false, false, true, true, false, false, true, true, false, false], [23.3394, 0.0910565])

########################
# inference
alpha = 1.0e-4 # learning rate
max_iter = 100000 # VI maximum iterations 

# learn variational parameters (mu & rho)
mu, rho = LogisticRegression.VI(Y, X, M, Sigma_w, alpha, max_iter)

########################

# inference

alpha = 1.0e-4 # learning rate

max_iter = 100000 # VI maximum iterations

# learn variational parameters (mu & rho)

mu, rho = LogisticRegression.VI(Y, X, M, Sigma_w, alpha, max_iter)

Out:([8.90405, -0.76043], [3.98836, -0.616809])

########################
# visualize (only for M=2)
visualize_surface(mu, rho, X, Y, "prediction")
visualize_contour(mu, rho, X, Y)
show()

########################

# visualize (only for M=2)

visualize_surface(mu, rho, X, Y, "prediction")

visualize_contour(mu, rho, X, Y)

show()

Science To Medicine

Just My Daily Study Note by ts.anesth.kpum