Reinforcement Learningについて体系的学習
テキストは「Pythonde学ぶ強化学習、著：久保孝宏」
——————————————-
時刻tにおける状態stの状態価値Vπ(st)を、「状態stを起点に、方策πに従って行動をとり続けて行った時の報酬の合計（すなわち）収益」と定義。

Vπ(st)=rt+1+γVπ(st+1)

つまり、ある時刻における価値関数は、その先の時刻における価値関数の漸化式になっているということ。

しかしながら、ある状態sから方策πにしたがって取る行動a（右に移動、それとも左、上、下？）は一義的に決まらない（確率分布）のである。実際には、確率分布にしたがって複数の行動候補から実際の行動が決定される。
現実の行動はどれか一つをとるが、価値関数は未来の収益を考えるため、枝分かれの全ての選択肢を考慮する必要がある。

状態sの時に戦略πに従って行動aをとったとき、それに対する結果、つまり対応する状態（s′）は一義的に決まらない（確率分布である）ために遷移確率（transition probability）を考える。行動a（右）を取ろうとしたのに、結果的に下に行ってしまうというのは「千鳥足状態！」。
Pass′=Pr{st+1=s′|st=s,at=a}、その際の報酬はRass′
——————————————-
状態価値関数　Vπに対するBellman方程式

価値関数は、直近の報酬に1ステップ先の価値関数を足したものである。ただし、方策および遷移確率で未来のとりうる値は枝分かれするので、その期待値をとる。

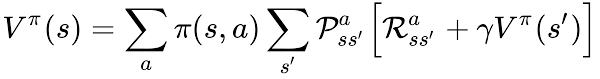
価値が最大になるように常に行動を選択する場合、戦略ではなくて、最大報酬を取ることとなり、

——————————————–
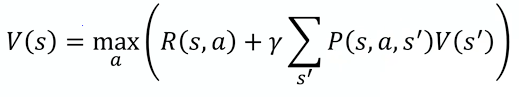
ともかく、bellman_equation.pyを実行してみる。main関数に出力が規程されているように

であれば、その価値は、

なんのこっちゃ、だけど、つまりstate=はじめの状態では、価値は0.7881、up、up選べば、0.9068まで価値が上がるが、down、 downと選ばれれば-.9606まで下がる。5回中、upが４回以上でhappy endの報酬１点がもらえるが、それ未満だとbad endで-1点となる。つまりdownが1回以上含まれていると価値は絶望的に低下し、逆に3回以上upがあればかなお駄賃１を貰えそうということなる。

とすると、価値の結果は以下の通り

——————————————–
実際には、Valueベースの方法では、価値を予め計算して、そのうちから最大のものを選択する必要がある。つまり、価値の計算が済みである必要があり、状態数が多いと非現実的となってくる。そこで動的計画法Dynamic Programming:DPでは適当なV(s’)を選択して、複数回、計算を繰り返す価値反復法Value Iterationで精度を上げる方法を取る。
精度については、更新前後の差（｜V_i+1(s)-V_i(s)｜）が一定値より小さいかで判定する。

Day2の最後は、Dynamic Programming Simulatorを仮想環境で作動させる。