Ref: Baysian Analysis with Python by Osvaldo Martin
?????????????????-
これまでのロジスティック回帰では、0か1かという2クラスを扱ってきたが、3つ以上のクラスを扱うソフトマックス回帰。
機械学習の分類に用いられてるやつだ!
ソフトマックス関数は、
softmax_i(μ) = exp(μ_i)/Σ exp(μ_k)
で、この関数のi番目の要素を和した左辺の合計は1となる(つまりK=1の場合は、ロジステック回帰!)。
ソフトマックス回帰では、ロジスティック回帰におけるベルヌイ分布(コイン投げ)への当てはめを、カテゴリカル分布(サイコロ投げ)に置き換える。
再び、IRISデータを用いる。3つのspecies(setosa, vesicolor, virginica)と、4つの特徴(sepal_length, sepal_width, petal_length, petal_width)を使って分析するが、データを平均値の差をとって標準化しておく。
|
1 2 3 4 5 |
iris = sns.load_dataset('iris') y_s = pd.Categorical(iris['species']).codes x_n = iris.columns[:-1] x_s = iris[x_n].values x_s = (x_s - x_s.mean(axis=0))/x_s.std(axis=0) |
このあと、import theano.tensor as ttで呼び出されているTheanoライブラリのソフトマックス関数を用いる。
αはそれぞれのspecies用に3つ確保。βは、それぞのれspecies3種と4つの特徴で3×4=12個。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
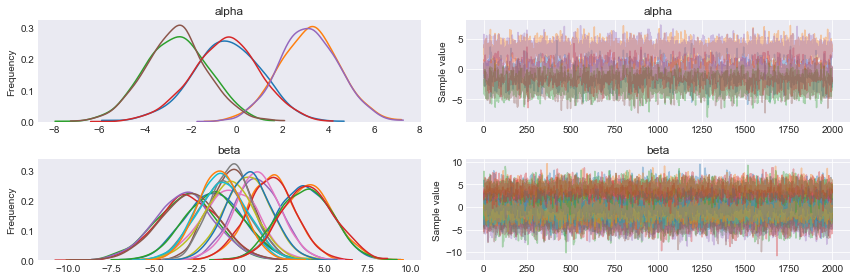
with pm.Model() as model_s: alpha = pm.Normal('alpha', mu=0, sd=2, shape=3) beta = pm.Normal('beta', mu=0, sd=2, shape=(4,3)) mu = alpha + pm.math.dot(x_s, beta) theta = tt.nnet.softmax(mu) yl = pm.Categorical('yl', p=theta, observed=y_s) trace_s = pm.sample(2000, njobs=1) pm.traceplot(trace_s) plt.figure() |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
pm.summary(trace_s, varnames) mean sd mc_error hpd_2.5 hpd_97.5 n_eff Rhat alpha__0 -0.48 1.52 0.03 -3.37 2.45 3799.44 1.0 alpha__1 3.11 1.30 0.03 0.52 5.56 3306.09 1.0 alpha__2 -2.67 1.40 0.03 -5.33 0.13 3566.79 1.0 beta__0_0 -1.49 1.69 0.03 -5.05 1.57 4407.36 1.0 beta__0_1 1.01 1.36 0.02 -1.79 3.54 3863.36 1.0 beta__0_2 0.50 1.37 0.02 -2.32 2.98 3868.32 1.0 beta__1_0 1.78 1.38 0.02 -0.74 4.65 3448.30 1.0 beta__1_1 -0.59 1.22 0.02 -2.91 1.85 3063.05 1.0 beta__1_2 -1.26 1.27 0.02 -3.76 1.16 3165.63 1.0 beta__2_0 -3.21 1.68 0.02 -6.59 0.01 4694.38 1.0 beta__2_1 -0.58 1.50 0.02 -3.47 2.37 4002.47 1.0 beta__2_2 3.80 1.61 0.03 0.64 6.85 4295.79 1.0 beta__3_0 -3.01 1.73 0.02 -6.42 0.33 5138.63 1.0 beta__3_1 -1.03 1.47 0.02 -3.81 1.86 3993.87 1.0 beta__3_2 3.97 1.53 0.02 1.03 6.98 3929.89 1.0 |
データの精度を、結果と観測値の比較において評価してみる。
|
1 2 3 4 5 6 7 |
data_pred = trace_s['alpha'].mean(axis=0) + np.dot(x_s, trace_s['beta'].mean(axis=0)) y_pred = [] for point in data_pred: y_pred.append(np.exp(point)/np.sum(np.exp(point), axis=0)) np.sum(y_s == np.argmax(y_pred, axis=1))/len(y_s) 0.9733333333333334 |
およそ98%の精度で分類できていることが解る。
ソフトマックス回帰モデルで、分類の一つは、他の分類にはまらないものとしてパラメータを固定した場合
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
data_pred = trace_s['alpha'].mean(axis=0) + np.dot(x_s, trace_s['beta'].mean(axis=0)) y_pred = [] for point in data_pred: y_pred.append(np.exp(point)/np.sum(np.exp(point), axis=0)) np.sum(y_s == np.argmax(y_pred, axis=1))/len(y_s) with pm.Model() as model_sf: alpha = pm.Normal('alpha', mu=0, sd=2, shape=2) beta = pm.Normal('beta', mu=0, sd=2, shape=(4,2)) alpha_f = tt.concatenate([[0] , alpha]) beta_f = tt.concatenate([np.zeros((4,1)) , beta], axis=1) mu = alpha_f + pm.math.dot(x_s, beta_f) theta = tt.nnet.softmax(mu) yl = pm.Categorical('yl', p=theta, observed=y_s) trace_sf = pm.sample(5000, njobs=1) pm.traceplot(trace_sf) plt.figure() |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
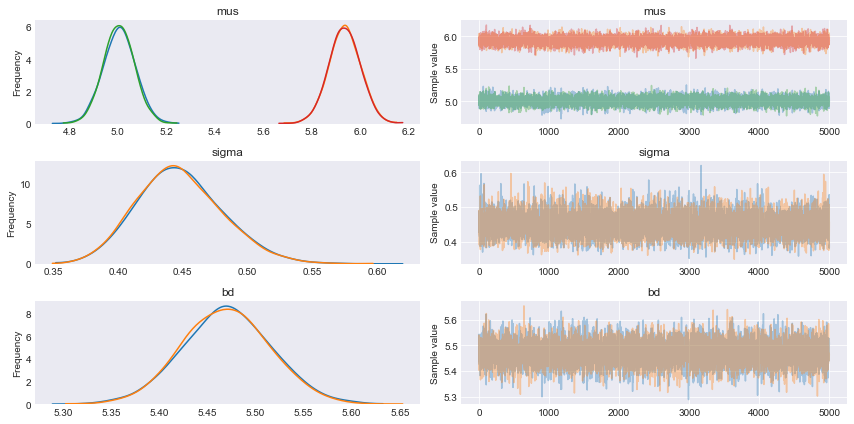
iris = sns.load_dataset("iris") df = iris.query("species == ('setosa', 'versicolor')") y_0 = pd.Categorical(df['species']).codes x_n = 'sepal_length' x_0 = df[x_n].values with pm.Model() as model_lda: mus = pm.Normal('mus', mu=0, sd=10, shape=2) sigma = pm.Uniform('sigma', 0, 10) setosa = pm.Normal('setosa', mu=mus[0], sd=sigma, observed=x_0[:50]) versicolor = pm.Normal('versicolor', mu=mus[1], sd=sigma, observed=x_0[50:]) bd = pm.Deterministic('bd', (mus[0]+mus[1])/2) trace_lda = pm.sample(5200, njobs=1) chain_lda = trace_lda[200:] pm.traceplot(chain_lda) plt.figure() |
|
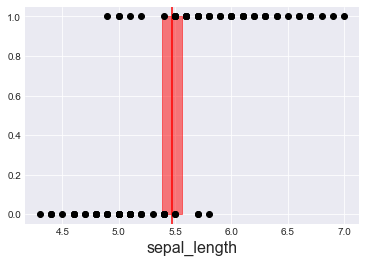
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
x_n = 'sepal_length' plt.axvline(trace_lda['bd'].mean(), ymax=1, color='r') bd_hpd = pm.hpd(trace_lda['bd']) plt.fill_betweenx([0, 1], bd_hpd[0], bd_hpd[1], color='r', alpha=0.5) plt.plot(x_0, y_0, 'o', color='k') plt.xlabel(x_n, fontsize=16) plt.figure() pm.summary(trace_lda) mean sd mc_error hpd_2.5 hpd_97.5 n_eff Rhat mus__0 5.01 0.06 5.68e-04 4.88 5.13 11366.83 1.0 mus__1 5.94 0.06 6.47e-04 5.81 6.06 9108.23 1.0 sigma 0.45 0.03 3.07e-04 0.39 0.51 11000.24 1.0 bd 5.47 0.05 4.66e-04 5.38 5.56 10919.89 1.0 |