Ref: Baysian Analysis with Python by Osvaldo Martin
?????????????????-
混合モデルMixture Model。異なる分布の混合からデータが発生している場合の解析を単純なモデルを組み合わせて行うのが混合モデル。
それぞれが正規分布するカテゴリカルなデータの組み合わせとして考える。最も単純な例では、コイン投げの問題、つまり表か裏かという2カテゴリーの場合は、ベルヌーイ分布をそれぞれの分布に当てはめて、事前分布には、β分布を用いた。このモデルを発展させて、3カテゴリー(例えば3面サイコロ)のそれぞれの目の出やすさの分布を考える。ベルヌーイ分布をkp個のパターンへと一般化したものがカテゴリカル分布であり、β分布を一般化したものがディリクレ分布である。
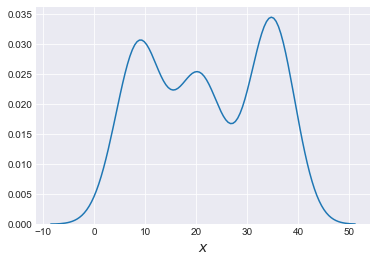
まずは3つの正規分布を混合して混合モデルのデータを作成する。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
import pymc3 as pm import numpy as np import pandas as pd import scipy.stats as stats import matplotlib.pyplot as plt import seaborn as sns plt.style.use('seaborn-darkgrid') np.set_printoptions(precision=2) clusters = 3 n_cluster = [80, 65, 90] n_total = sum(n_cluster) means = [9, 21, 35] std_devs = [2, 2, 2] mix = np.random.normal(np.repeat(means, n_cluster), np.repeat(std_devs, n_cluster)) sns.kdeplot(np.array(mix)) plt.xlabel('$x$', fontsize=14) plt.figure() |
k=3のディリクレ分布については、以下の三角図に描画される。特徴として三角形内に位置する点の3つの座標値の和は、1となることである。

平均と標準偏差が既知の正規分布混合モデルを出力すると、
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
with pm.Model() as model_kg: p = pm.Dirichlet('p', a=np.ones(clusters)) category = pm.Categorical('category', p=p, shape=n_total) means = pm.math.constant([10, 20, 35]) y = pm.Normal('y', mu=means[category], sd=2, observed=mix) trace_kg = pm.sample(10000, njobs=1) chain_kg = trace_kg[1000:] varnames_kg = ['p'] pm.traceplot(chain_kg, varnames_kg) plt.figure() |
次に3つの平均、一つの共有標準偏差の正規分布混合モデルを出力する。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
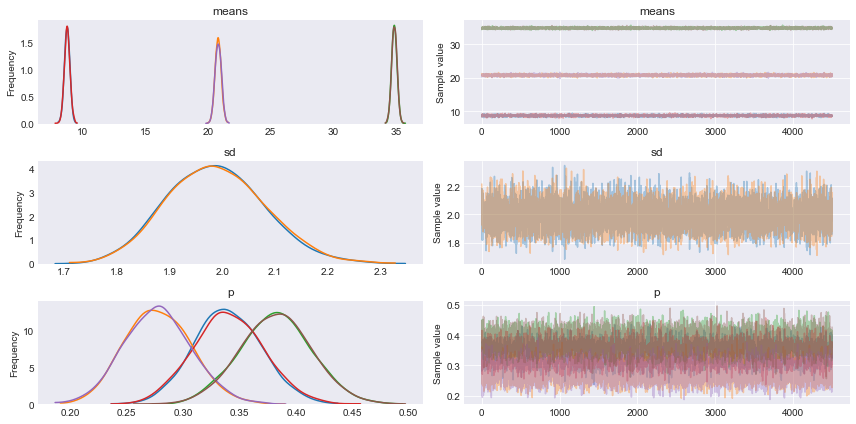
with pm.Model() as model_ug: p = pm.Dirichlet('p', a=np.ones(clusters)) category = pm.Categorical('category', p=p, shape=n_total) means = pm.Normal('means', mu=[10, 20, 35], sd=2, shape=clusters) sd = pm.HalfCauchy('sd', 5) y = pm.Normal('y', mu=means[category], sd=sd, observed=mix) trace_ug = pm.sample(10000, njobs=1) chain_ug = trace_ug[1000:] varnames_ug = ['means', 'sd', 'p'] pm.traceplot(chain_ug, varnames_ug) plt.figure() |
統計の要約量は
|
1 2 3 4 5 6 7 8 9 10 |
pm.summary(chain_ug, varnames_ug) mean sd mc_error hpd_2.5 hpd_97.5 n_eff Rhat means__0 8.759047 0.222475 0.001254 8.335419 9.198001 22859.140945 0.999945 means__1 20.809100 0.243831 0.001484 20.340467 21.295300 22642.766916 1.000163 means__2 34.870334 0.207167 0.001645 34.471929 35.285050 15782.883868 1.000126 sd 1.988366 0.093136 0.000601 1.804096 2.166910 23114.884570 0.999952 p__0 0.340627 0.030837 0.000196 0.281629 0.402447 28036.508484 0.999949 p__1 0.277165 0.029061 0.000201 0.221133 0.334732 21760.903129 0.999944 p__2 0.382208 0.031464 0.000217 0.318735 0.443395 22601.776832 0.999949 |
となる。
この混合モデルを出力すれば、
|
1 2 3 4 5 6 7 8 |
ppc = pm.sample_ppc(chain_ug, 50, model_ug) for i in ppc['y']: sns.kdeplot(i, alpha=0.1, color='b') sns.kdeplot(np.array(mix), lw=2, color='k') plt.xlabel('$x$', fontsize=14) plt.figure() |
離散的な潜在変数zについて、周辺化された混合モデルに変更すると、
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
with pm.Model() as model_mg: p = pm.Dirichlet('p', a=np.ones(clusters)) #category = pm.Categorical('category', p=p, shape=n_total) means = pm.Normal('means', mu=[10, 20, 35], sd=2, shape=clusters) sd = pm.HalfCauchy('sd', 5) y = pm.NormalMixture('y', w=p, mu=means, sd=sd, observed=mix) #y = pm.Normal('y', mu=means[category], sd=sd, observed=mix) trace_mg = pm.sample(5000, njobs=1) chain_mg = trace_mg[500:] varnames_mg = ['means', 'sd', 'p'] pm.traceplot(chain_mg, varnames_mg); plt.figure() |