Ref: Baysian Analysis with Python by Osvaldo Martin
????????
多重ロジスティック回帰で、複数個の独立変数を組み込んで、回帰を行う。
先の菖蒲の学習用分類データを用いて、sepal_length(ガク片の長さ)とsepal_width(ガク片の幅)から、菖蒲の分類を行う。
|
1 2 3 4 5 6 |
sepal_length sepal_width petal_length petal_width species 0 5.1 3.5 1.4 0.2 setosa 1 4.9 3.0 1.4 0.2 setosa 2 4.7 3.2 1.3 0.2 setosa 3 4.6 3.1 1.5 0.2 setosa 4 5.0 3.6 1.4 0.2 setosa |
ロジスティック解析モデルで、境界決定は、
θ = logistic(α + β0x0 + β1x1)
α + β0x0 + β1x1 = 0 のとき、
logistic(α + β0x0 + β1x1)= 0.5
から
x1 = -α/β1 + (-β0/β1 * x0 )
となり、第一項 -α/β1がY切片、第二項係数-β0/β1 が傾き
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
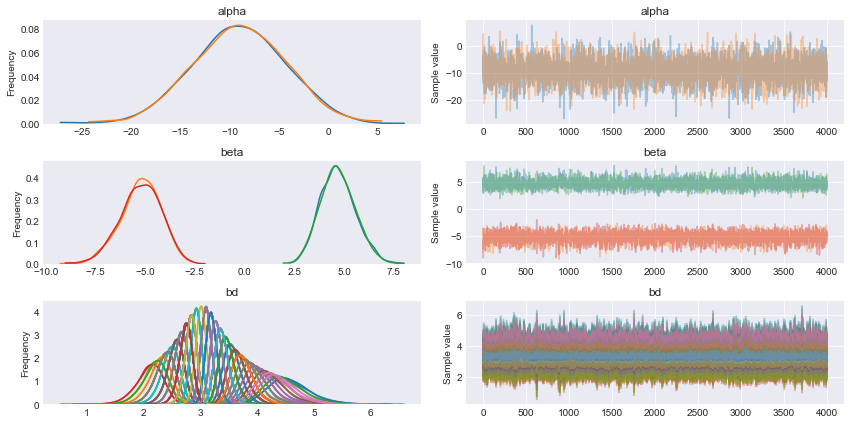
df = iris.query("species == ('setosa', 'versicolor')") y_1 = pd.Categorical(df['species']).codes x_n = ['sepal_length', 'sepal_width'] x_1 = df[x_n].values with pm.Model() as model_1: alpha = pm.Normal('alpha', mu=0, sd=10) beta = pm.Normal('beta', mu=0, sd=2, shape=len(x_n)) mu = alpha + pm.math.dot(x_1, beta) theta = 1 / (1 + pm.math.exp(-mu)) bd = pm.Deterministic('bd', -alpha/beta[1] - beta[0]/beta[1] * x_1[:,0]) yl = pm.Bernoulli('yl', p=theta, observed=y_1) trace_1 = pm.sample(5000, njobs=1) chain_1 = trace_1[1000:] varnames = ['alpha', 'beta', 'bd'] pm.traceplot(chain_1, varnames) plt.figure() |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
idx = np.argsort(x_1[:,0]) ld = chain_1['bd'].mean(0)[idx] plt.scatter(x_1[:,0], x_1[:,1], c=y_0, cmap='viridis') plt.plot(x_1[:,0][idx], ld, color='r'); ld_hpd = pm.hpd(chain_1['bd'])[idx] plt.fill_between(x_1[:,0][idx], ld_hpd[:,0], ld_hpd[:,1], color='r', alpha=0.5); plt.xlabel(x_n[0], fontsize=16) plt.ylabel(x_n[1], fontsize=16) plt.figure() |
|
1 2 3 4 5 |
corr = iris[iris['species'] != 'virginica'].corr() mask = np.tri(*corr.shape).T sns.heatmap(corr.abs(), mask=mask, annot=True, cmap='viridis') plt.figure() |