Ref: Baysian Analysis with Python by Osvaldo Martin
—————————————————-
ロジスティック回帰
ある現象の発生確率p(X)を調べる。その発生原因となりうる要素(因子、独立変数、説明変数)をX=(x1, x2, x3,….,xn)とする。
Xが発生したときの事後確率でp(X)を表現すると、
p(X) = Probability(発生|X)
となり、Fでp(X)をモデル化すると、ロジスティック関数を用いて、
f = 1 / (1 + exp(-r))
Z = α + β1*x1 + β2*x2+……+βn*xn と線形結合で表現すると、
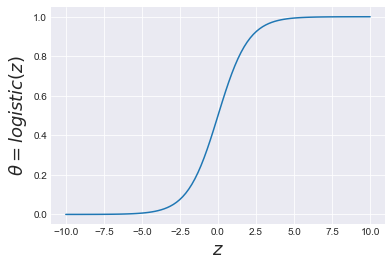
logistic(Z) = 1 / (1 + exp(-Z))
Z = 0 ならば、logistic(Z)=logistic(0) = 1 / (1 + exp(-0)) = 1/2 = 0.5
Z = ∞ならば、logistic(Z)=logistic(∞) = 1 / (1 + exp(-∞)) ≒ 1/1 = 1
Z =-∞ならば、logistic(Z)=logistic(-∞) = 1 / (1 + exp(∞)) ≒ 1/∞ ≒ 0
ロジスティック関数の特徴は、その引数の値Zに関わらず、0〜1の値を返す。
発生する確率 p(X) = 1 / (1 + exp(-Z))
発生しない確率 1- p(X) = 1 – 1 / (1 + exp(-Z)) = (((1 + exp(-Z)) – 1 ) / (1 + exp(-Z))
= exp(-Z) / (1 + exp(-Z))
最後は、起こるか、起こらないかという、ベルヌーイ分布[0,1]に当てはめる。
要するに、線形回帰の結果を[0,1]の範囲内に収めるために、ロジスティック関数を逆連結関数として用いているということ。
発生する確率と発生しない確率の比は、オッズ
p(X)/(1 – p(X)) = [1 / (1 + exp(-Z))] / [exp(-Z) / (1 + exp(-Z))]
= [1 / (1 + exp(-Z))] * [(1 + exp(-Z))/exp(-Z)]
= 1 / exp(-Z)
= exp(Z)
= exp(α + β1*x1 + β2*x2+……+βn*xn)
オッズのログをとると、
log{p(X)/(1- p(X))} = α + β1*x1 + β2*x2+……+βn*xn と、重回帰分析と同じ形になる。
回帰式が直線単回帰の場合、 Z=α+βx となり
logistic (Z) = logistic(α+βx) = θ ー> y〜Bernoulli(θ)
Bayesを用いたロジスティック回帰モデルとしては、
回帰係数αの事前分布はNormal(μα,σα)、βの事前分布は、Normal(0,σβ)
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
import pymc3 as pm import numpy as np import pandas as pd import scipy.stats as stats import matplotlib.pyplot as plt import seaborn as sns import theano.tensor as tt plt.style.use('seaborn-darkgrid') np.set_printoptions(precision=2) pd.set_option('display.precision', 2) z = np.linspace(-10, 10, 100) logistic = 1 / (1 + np.exp(-z)) plt.plot(z, logistic) plt.xlabel('$z$', fontsize=18) plt.ylabel('θ=$logistic(z)$', fontsize=18) plt.figure() |
Iris data setで:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
iris = sns.load_dataset('iris') iris.head() sepal_length sepal_width petal_length petal_width species 0 5.1 3.5 1.4 0.2 setosa 1 4.9 3.0 1.4 0.2 setosa 2 4.7 3.2 1.3 0.2 setosa 3 4.6 3.1 1.5 0.2 setosa 4 5.0 3.6 1.4 0.2 setosa iris.tail() sepal_length sepal_width petal_length petal_width species 145 6.7 3.0 5.2 2.3 virginica 146 6.3 2.5 5.0 1.9 virginica 147 6.5 3.0 5.2 2.0 virginica 148 6.2 3.4 5.4 2.3 virginica 149 5.9 3.0 5.1 1.8 virginica |
Irisデータは、3種類の種、それぞれ50個、全部で150列、一列5データで、全部で750データとなる。
|
1 2 3 |
iris.size 750 |
|
1 2 3 |
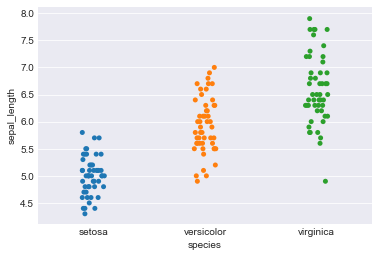
sns.stripplot(x="species", y="sepal_length", data=iris, jitter=True) plt.figure() |
|
1 2 3 |
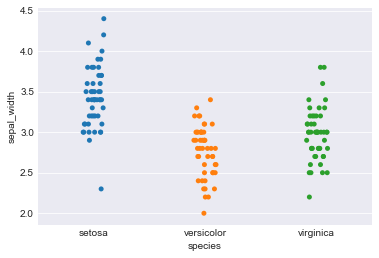
sns.stripplot(x="species", y="sepal_width", data=iris, jitter=True) plt.figure() |
|
1 2 3 |
sns.stripplot(x="species", y="petal_length", data=iris, jitter=True) plt.figure() |
|
1 2 3 |
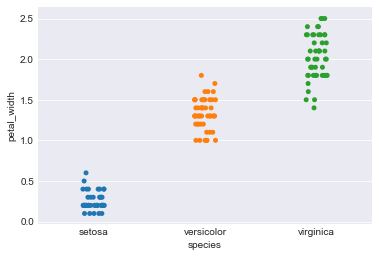
sns.stripplot(x="species", y="petal_width", data=iris, jitter=True) plt.figure() |
|
1 2 3 |
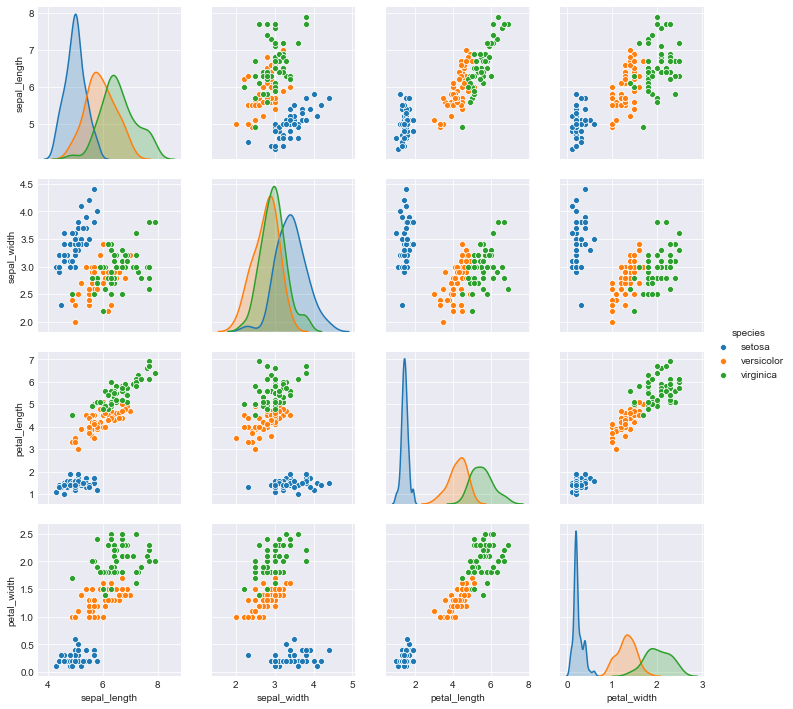
sns.pairplot(iris, hue='species', diag_kind='kde') plt.figure() |
分類の問題として、菖蒲の種’setosa’と’versicolor’をそれぞれ0と1として、sepal_lengthを独立変数としてロジスティックモデルを構築。
|
1 2 3 4 |
df = iris.query("species == ('setosa', 'versicolor')") y_0 = pd.Categorical(df['species']).codes x_n = 'sepal_length' x_0 = df[x_n].values |
αの事前分布を平均値0、標準偏差10、βの事前分布を平均値0、標準偏差10として
μ= α + β * X, θ = 1 / (1 + 1 / exp(μ)), ベルヌイ関数(θ)として事後分布を求めてみる。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
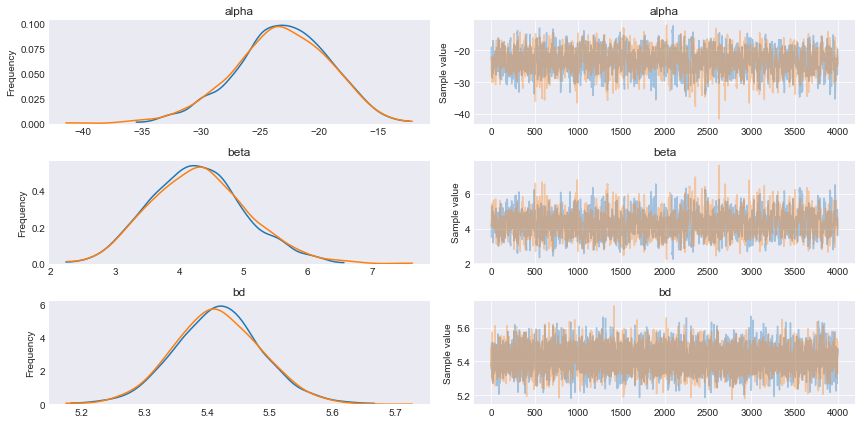
with pm.Model() as model_0: alpha = pm.Normal('alpha', mu=0, sd=10) beta = pm.Normal('beta', mu=0, sd=10) mu = alpha + pm.math.dot(x_0, beta) theta = pm.Deterministic('theta', 1 / (1 + pm.math.exp(-mu))) bd = pm.Deterministic('bd', -alpha/beta) yl = pm.Bernoulli('yl', p=theta, observed=y_0) trace_0 = pm.sample(5000) chain_0 = trace_0[1000:] varnames = ['alpha', 'beta', 'bd'] pm.traceplot(chain_0, varnames) plt.figure() |
|
1 2 3 4 5 6 |
pm.summary(chain_0, varnames) mean sd mc_error hpd_2.5 hpd_97.5 n_eff Rhat alpha -23.24 4.02 1.09e-01 -30.80 -15.31 1265.02 1.0 beta 4.29 0.75 2.02e-02 2.84 5.72 1262.64 1.0 bd 5.42 0.07 8.60e-04 5.28 5.56 6929.13 1.0 |
θ=0.5のときのx1 = -α/βは、5.42。
では、事前分布を少しいじくって、
αの事前分布を平均値0、標準偏差5、βの事前分布を平均値0、標準偏差5として
μ= α + β * X, θ = 1 / (1 + 1 / exp(μ)), ベルヌイ関数(θ)として事後分布を求めてみる。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
with pm.Model() as model_0: alpha = pm.Normal('alpha', mu=0, sd=5) beta = pm.Normal('beta', mu=0, sd=5) mu = alpha + pm.math.dot(x_0, beta) theta = pm.Deterministic('theta', 1 / (1 + pm.math.exp(-mu))) bd = pm.Deterministic('bd', -alpha/beta) yl = pm.Bernoulli('yl', p=theta, observed=y_0) trace_1 = pm.sample(5000) chain_1 = trace_1[1000:] varnames = ['alpha', 'beta', 'bd'] pm.traceplot(chain_1, varnames) plt.figure() |
|
1 2 3 4 5 6 |
pm.summary(chain_1, varnames) mean sd mc_error hpd_2.5 hpd_97.5 n_eff Rhat alpha -16.64 2.76 7.17e-02 -22.25 -11.48 1360.03 1.0 beta 3.07 0.51 1.32e-02 2.15 4.14 1376.66 1.0 bd 5.42 0.09 1.05e-03 5.24 5.58 6625.46 1.0 |
αもβも少し0に近づいた。
一方で、θ=0.5のときのx1 = -α/βは、5.42で変わらない。
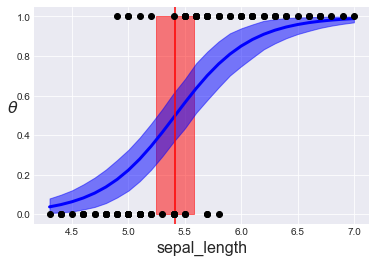
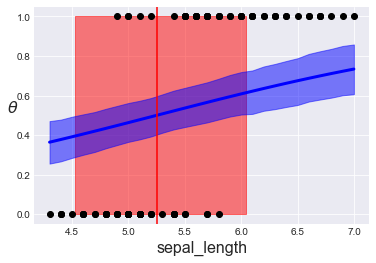
推定されたロジスティック回帰モデルのシグモイド曲線、境界決定、その95%HPDは、α、βの標準偏差10のとき、
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
theta = chain_0['theta'].mean(axis=0) idx = np.argsort(x_0) plt.plot(x_0[idx], theta[idx], color='b', lw=3); plt.axvline(chain_0['bd'].mean(), ymax=1, color='r') bd_hpd = pm.hpd(chain_0['bd']) plt.fill_betweenx([0, 1], bd_hpd[0], bd_hpd[1], color='r', alpha=0.5) plt.plot(x_0, y_0, 'o', color='k') theta_hpd = pm.hpd(chain_0['theta'])[idx] plt.fill_between(x_0[idx], theta_hpd[:,0], theta_hpd[:,1], color='b', alpha=0.5) plt.xlabel(x_n, fontsize=16) plt.ylabel(r'$\theta$', rotation=0, fontsize=16) plt.figure() |
推定されたロジスティック回帰モデルのシグモイド曲線、境界決定、その95%HPDは、α、βの標準偏差5のときは、
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
theta = chain_1['theta'].mean(axis=0) idx = np.argsort(x_0) plt.plot(x_0[idx], theta[idx], color='b', lw=3); plt.axvline(chain_1['bd'].mean(), ymax=1, color='r') bd_hpd = pm.hpd(chain_1['bd']) plt.fill_betweenx([0, 1], bd_hpd[0], bd_hpd[1], color='r', alpha=0.5) plt.plot(x_0, y_0, 'o', color='k') theta_hpd = pm.hpd(chain_1['theta'])[idx] plt.fill_between(x_0[idx], theta_hpd[:,0], theta_hpd[:,1], color='b', alpha=0.5) plt.xlabel(x_n, fontsize=16) plt.ylabel(r'$\theta$', rotation=0, fontsize=16) plt.figure() |
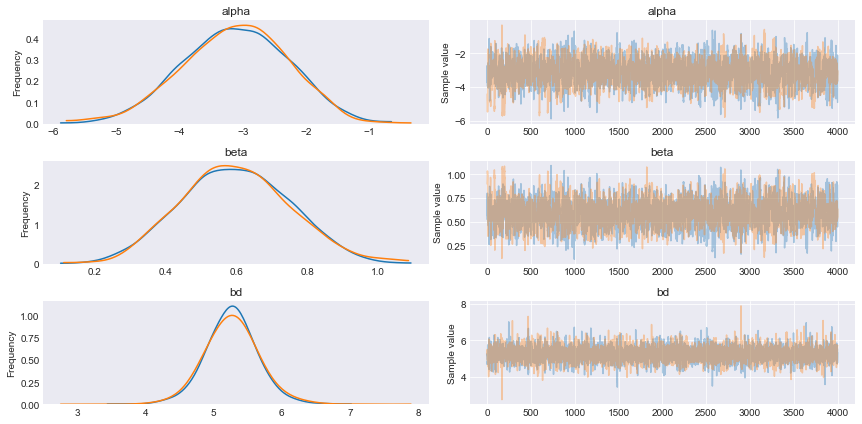
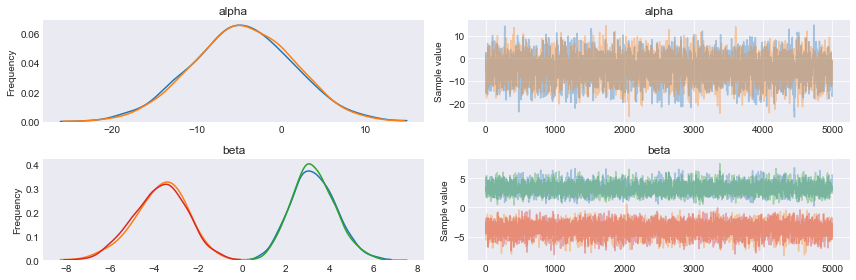
では、ちょっと極端な例として、αの事前分布を平均値0、標準偏差1、βの事前分布を平均値0、標準偏差1として、ほとんどばらつきのない状態で推定されたロジスティック回帰モデルのシグモイド曲線、境界決定、その95%HPDを見てみる、
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
with pm.Model() as model_0: alpha = pm.Normal('alpha', mu=0, sd=1) beta = pm.Normal('beta', mu=0, sd=1) mu = alpha + pm.math.dot(x_0, beta) theta = pm.Deterministic('theta', 1 / (1 + pm.math.exp(-mu))) bd = pm.Deterministic('bd', -alpha/beta) yl = pm.Bernoulli('yl', p=theta, observed=y_0) trace_2 = pm.sample(5000) chain_2 = trace_2[1000:] varnames = ['alpha', 'beta', 'bd'] pm.traceplot(chain_2, varnames) plt.figure() |
|
1 2 3 4 5 6 |
pm.summary(chain_2, varnames) mean sd mc_error hpd_2.5 hpd_97.5 n_eff Rhat alpha -3.13 0.83 2.26e-02 -4.73 -1.56 1543.52 1.0 beta 0.60 0.15 4.16e-03 0.30 0.89 1545.62 1.0 bd 5.26 0.38 4.61e-03 4.53 6.04 6620.96 1.0 |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
theta = chain_2['theta'].mean(axis=0) idx = np.argsort(x_0) plt.plot(x_0[idx], theta[idx], color='b', lw=3); plt.axvline(chain_2['bd'].mean(), ymax=1, color='r') bd_hpd = pm.hpd(chain_2['bd']) plt.fill_betweenx([0, 1], bd_hpd[0], bd_hpd[1], color='r', alpha=0.5) plt.plot(x_0, y_0, 'o', color='k') theta_hpd = pm.hpd(chain_2['theta'])[idx] plt.fill_between(x_0[idx], theta_hpd[:,0], theta_hpd[:,1], color='b', alpha=0.5) plt.xlabel(x_n, fontsize=16) plt.ylabel(r'$\theta$', rotation=0, fontsize=16) plt.figure() |
setosaの45個のデータを削って、アンバランスなクラス設定にしてみると、
|
1 2 3 4 5 6 7 |
df = iris.query("species == ('setosa', 'versicolor')") df = df[45:] # df[22:78] y_3 = pd.Categorical(df['species']).codes x_n = ['sepal_length', 'sepal_width'] x_3 = df[x_n].values df |
以下のように、setosaが5つしか無いが、vesicolorは50個ある。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 |
sepal_length sepal_width petal_length petal_width species 45 4.8 3.0 1.4 0.3 setosa 46 5.1 3.8 1.6 0.2 setosa 47 4.6 3.2 1.4 0.2 setosa 48 5.3 3.7 1.5 0.2 setosa 49 5.0 3.3 1.4 0.2 setosa 50 7.0 3.2 4.7 1.4 versicolor 51 6.4 3.2 4.5 1.5 versicolor 52 6.9 3.1 4.9 1.5 versicolor 53 5.5 2.3 4.0 1.3 versicolor 54 6.5 2.8 4.6 1.5 versicolor 55 5.7 2.8 4.5 1.3 versicolor 56 6.3 3.3 4.7 1.6 versicolor 57 4.9 2.4 3.3 1.0 versicolor 58 6.6 2.9 4.6 1.3 versicolor 59 5.2 2.7 3.9 1.4 versicolor 60 5.0 2.0 3.5 1.0 versicolor 61 5.9 3.0 4.2 1.5 versicolor 62 6.0 2.2 4.0 1.0 versicolor 63 6.1 2.9 4.7 1.4 versicolor 64 5.6 2.9 3.6 1.3 versicolor 65 6.7 3.1 4.4 1.4 versicolor 66 5.6 3.0 4.5 1.5 versicolor 67 5.8 2.7 4.1 1.0 versicolor 68 6.2 2.2 4.5 1.5 versicolor 69 5.6 2.5 3.9 1.1 versicolor 70 5.9 3.2 4.8 1.8 versicolor 71 6.1 2.8 4.0 1.3 versicolor 72 6.3 2.5 4.9 1.5 versicolor 73 6.1 2.8 4.7 1.2 versicolor 74 6.4 2.9 4.3 1.3 versicolor 75 6.6 3.0 4.4 1.4 versicolor 76 6.8 2.8 4.8 1.4 versicolor 77 6.7 3.0 5.0 1.7 versicolor 78 6.0 2.9 4.5 1.5 versicolor 79 5.7 2.6 3.5 1.0 versicolor 80 5.5 2.4 3.8 1.1 versicolor 81 5.5 2.4 3.7 1.0 versicolor 82 5.8 2.7 3.9 1.2 versicolor 83 6.0 2.7 5.1 1.6 versicolor 84 5.4 3.0 4.5 1.5 versicolor 85 6.0 3.4 4.5 1.6 versicolor 86 6.7 3.1 4.7 1.5 versicolor 87 6.3 2.3 4.4 1.3 versicolor 88 5.6 3.0 4.1 1.3 versicolor 89 5.5 2.5 4.0 1.3 versicolor 90 5.5 2.6 4.4 1.2 versicolor 91 6.1 3.0 4.6 1.4 versicolor 92 5.8 2.6 4.0 1.2 versicolor 93 5.0 2.3 3.3 1.0 versicolor 94 5.6 2.7 4.2 1.3 versicolor 95 5.7 3.0 4.2 1.2 versicolor 96 5.7 2.9 4.2 1.3 versicolor 97 6.2 2.9 4.3 1.3 versicolor 98 5.1 2.5 3.0 1.1 versicolor 99 5.7 2.8 4.1 1.3 versicolor |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
with pm.Model() as model_3: alpha = pm.Normal('alpha', mu=0, sd=10) beta = pm.Normal('beta', mu=0, sd=2, shape=len(x_n)) mu = alpha + pm.math.dot(x_3, beta) p = 1 / (1 + pm.math.exp(-mu)) ld = pm.Deterministic('ld', -alpha/beta[1] - beta[0]/beta[1] * x_3[:,0]) yl = pm.Bernoulli('yl', p=p, observed=y_3) trace_4 = pm.sample(5000) cadena_4 = trace_4[:] varnames = ['alpha', 'beta'] pm.traceplot(cadena_4, varnames); plt.figure() |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
df = iris.query("species == ('setosa', 'versicolor')") df = df[45:] # df[22:78] y_3 = pd.Categorical(df['species']).codes x_n = ['sepal_length', 'sepal_width'] x_3 = df[x_n].values with pm.Model() as model_3: alpha = pm.Normal('alpha', mu=0, sd=10) beta = pm.Normal('beta', mu=0, sd=2, shape=len(x_n)) mu = alpha + pm.math.dot(x_3, beta) p = 1 / (1 + pm.math.exp(-mu)) ld = pm.Deterministic('ld', -alpha/beta[1] - beta[0]/beta[1] * x_3[:,0]) yl = pm.Bernoulli('yl', p=p, observed=y_3) trace_4 = pm.sample(5000) cadena_4 = trace_4[:] varnames = ['alpha', 'beta'] pm.traceplot(cadena_4, varnames); plt.figure() <a href="http://anesth-kpum.org/blog_ts/wp-content/uploads/2019/02/image-65.png"><img src="http://anesth-kpum.org/blog_ts/wp-content/uploads/2019/02/image-65.png" alt="" width="377" height="263" class="alignnone size-full wp-image-2656" /></a> |
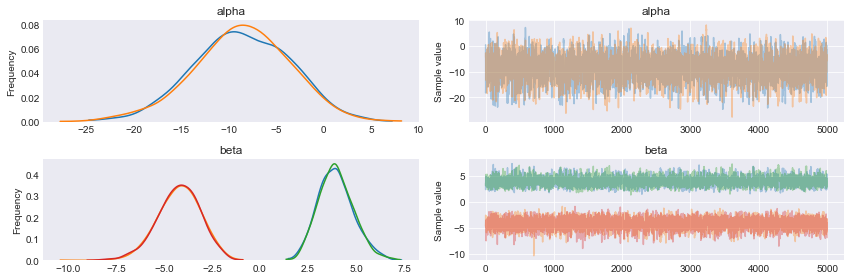
次に、同じ削るにしても、setosaとvesicolorを平等に22ずつ削ってみると、
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
df = iris.query("species == ('setosa', 'versicolor')") df = df[22:78] y_3 = pd.Categorical(df['species']).codes x_n = ['sepal_length', 'sepal_width'] x_3 = df[x_n].values with pm.Model() as model_3: alpha = pm.Normal('alpha', mu=0, sd=10) beta = pm.Normal('beta', mu=0, sd=2, shape=len(x_n)) mu = alpha + pm.math.dot(x_3, beta) p = 1 / (1 + pm.math.exp(-mu)) ld = pm.Deterministic('ld', -alpha/beta[1] - beta[0]/beta[1] * x_3[:,0]) yl = pm.Bernoulli('yl', p=p, observed=y_3) trace_5 = pm.sample(5000) cadena_5 = trace_5[:] varnames = ['alpha', 'beta'] pm.traceplot(cadena_5, varnames); plt.figure() |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 |
df sepal_length sepal_width petal_length petal_width species 22 4.6 3.6 1.0 0.2 setosa 23 5.1 3.3 1.7 0.5 setosa 24 4.8 3.4 1.9 0.2 setosa 25 5.0 3.0 1.6 0.2 setosa 26 5.0 3.4 1.6 0.4 setosa 27 5.2 3.5 1.5 0.2 setosa 28 5.2 3.4 1.4 0.2 setosa 29 4.7 3.2 1.6 0.2 setosa 30 4.8 3.1 1.6 0.2 setosa 31 5.4 3.4 1.5 0.4 setosa 32 5.2 4.1 1.5 0.1 setosa 33 5.5 4.2 1.4 0.2 setosa 34 4.9 3.1 1.5 0.2 setosa 35 5.0 3.2 1.2 0.2 setosa 36 5.5 3.5 1.3 0.2 setosa 37 4.9 3.6 1.4 0.1 setosa 38 4.4 3.0 1.3 0.2 setosa 39 5.1 3.4 1.5 0.2 setosa 40 5.0 3.5 1.3 0.3 setosa 41 4.5 2.3 1.3 0.3 setosa 42 4.4 3.2 1.3 0.2 setosa 43 5.0 3.5 1.6 0.6 setosa 44 5.1 3.8 1.9 0.4 setosa 45 4.8 3.0 1.4 0.3 setosa 46 5.1 3.8 1.6 0.2 setosa 47 4.6 3.2 1.4 0.2 setosa 48 5.3 3.7 1.5 0.2 setosa 49 5.0 3.3 1.4 0.2 setosa 50 7.0 3.2 4.7 1.4 versicolor 51 6.4 3.2 4.5 1.5 versicolor 52 6.9 3.1 4.9 1.5 versicolor 53 5.5 2.3 4.0 1.3 versicolor 54 6.5 2.8 4.6 1.5 versicolor 55 5.7 2.8 4.5 1.3 versicolor 56 6.3 3.3 4.7 1.6 versicolor 57 4.9 2.4 3.3 1.0 versicolor 58 6.6 2.9 4.6 1.3 versicolor 59 5.2 2.7 3.9 1.4 versicolor 60 5.0 2.0 3.5 1.0 versicolor 61 5.9 3.0 4.2 1.5 versicolor 62 6.0 2.2 4.0 1.0 versicolor 63 6.1 2.9 4.7 1.4 versicolor 64 5.6 2.9 3.6 1.3 versicolor 65 6.7 3.1 4.4 1.4 versicolor 66 5.6 3.0 4.5 1.5 versicolor 67 5.8 2.7 4.1 1.0 versicolor 68 6.2 2.2 4.5 1.5 versicolor 69 5.6 2.5 3.9 1.1 versicolor 70 5.9 3.2 4.8 1.8 versicolor 71 6.1 2.8 4.0 1.3 versicolor 72 6.3 2.5 4.9 1.5 versicolor 73 6.1 2.8 4.7 1.2 versicolor 74 6.4 2.9 4.3 1.3 versicolor 75 6.6 3.0 4.4 1.4 versicolor 76 6.8 2.8 4.8 1.4 versicolor 77 6.7 3.0 5.0 1.7 versicolor |
|
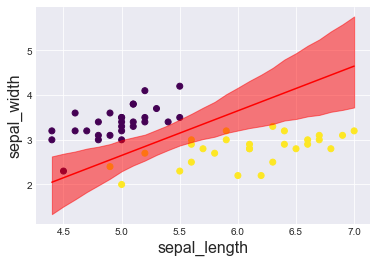
1 2 3 4 5 6 7 8 9 10 11 12 |
idx = np.argsort(x_3[:,0]) ld = trace_5['ld'].mean(0)[idx] plt.scatter(x_3[:,0], x_3[:,1], c=y_3, cmap='viridis') plt.plot(x_3[:,0][idx], ld, color='r'); ld_hpd = pm.hpd(trace_5['ld'])[idx] plt.fill_between(x_3[:,0][idx], ld_hpd[:,0], ld_hpd[:,1], color='r', alpha=0.5); plt.xlabel(x_n[0], fontsize=16) plt.ylabel(x_n[1], fontsize=16) plt.figure() |