Ref: Baysian Analysis with Python by Osvaldo Martin
—————————————————-
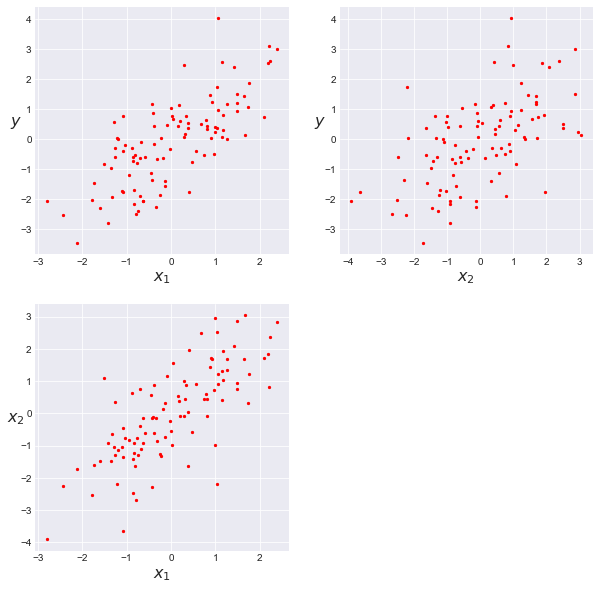
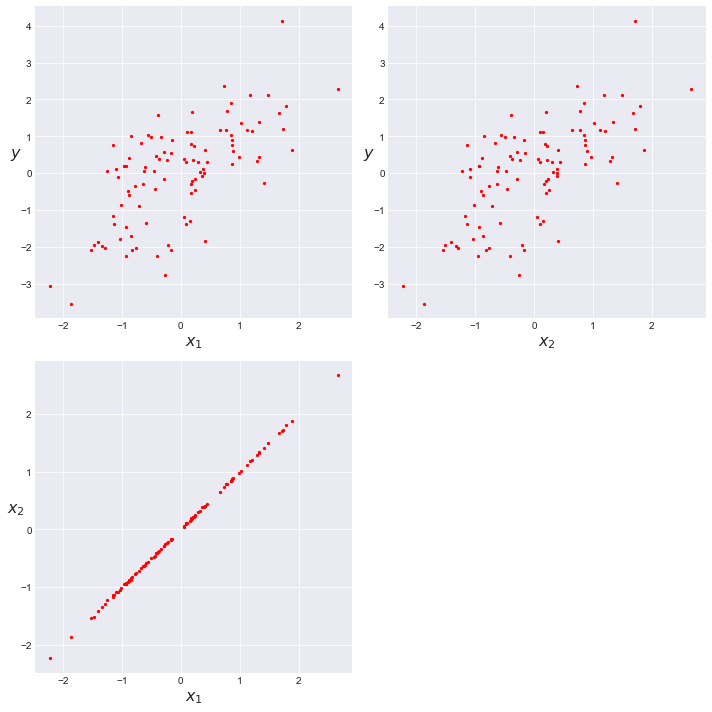
交絡(Confounding)は、統計モデルの中の従属変数と独立変数の両方に相関する外部変数が存在することであり、そのような外部変数を交絡変数(confounding variable)と呼ぶ。
|
1 2 3 4 5 6 7 8 9 |
np.random.seed(123) N = 100 x_1 = np.random.normal(size=N) x_2 = x_1 + np.random.normal(size=N, scale=1) y = x_1 + np.random.normal(size=N) X = np.vstack((x_1, x_2)) scatter_plot(X, y) plt.figure() |
|
1 2 3 4 5 6 7 8 9 10 11 12 |
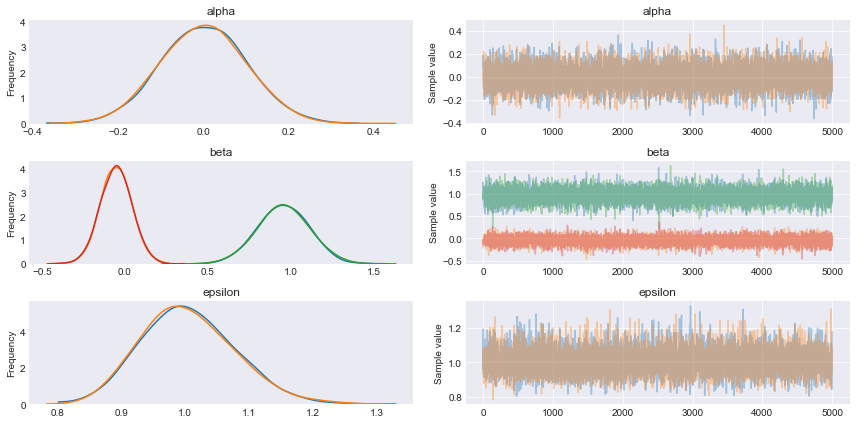
with pm.Model() as model_red: alpha = pm.Normal('alpha', mu=0, sd=1) beta = pm.Normal('beta', mu=0, sd=10, shape=2) epsilon = pm.HalfCauchy('epsilon', 5) mu = alpha + pm.math.dot(beta, X) y_pred = pm.Normal('y_pred', mu=mu, sd=epsilon, observed=y) trace_red = pm.sample(5000, njobs=1) pm.traceplot(trace_red) plt.figure() |
|
1 2 3 4 5 6 7 |
pm.summary(trace_red) mean sd mc_error hpd_2.5 hpd_97.5 n_eff Rhat alpha -0.09 0.10 1.12e-03 -0.29 0.10 8667.38 1.0 beta__0 0.92 0.13 1.33e-03 0.66 1.18 8604.50 1.0 beta__1 0.02 0.10 1.08e-03 -0.17 0.24 8664.55 1.0 epsilon 0.99 0.07 7.66e-04 0.85 1.14 8879.35 1.0 |
with pm.Model() as model_red:
alpha = pm.Normal(‘alpha’, mu=0, sd=1)
#beta = pm.Normal(‘beta’, mu=0, sd=10, shape=2)
beta = pm.Normal(‘beta’, mu=0, sd=10)
epsilon = pm.HalfCauchy(‘epsilon’, 5)
#mu = alpha + pm.math.dot(beta, X)
mu = alpha + beta * X[0]
y_pred = pm.Normal(‘y_pred’, mu=mu, sd=epsilon, observed=y)
trace_red = pm.sample(5000, njobs=1)
pm.traceplot(trace_red)
plt.savefig(‘img428.png’, dpi=300, figsize=(5.5, 5.5))
plt.figure()
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
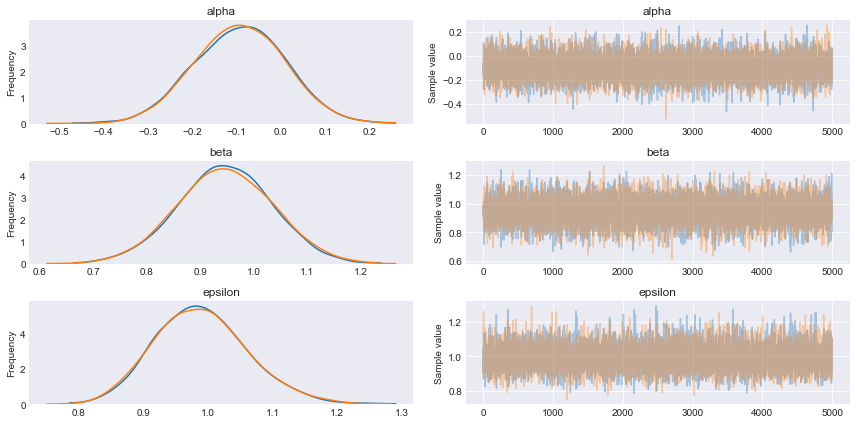
with pm.Model() as model_red: alpha = pm.Normal('alpha', mu=0, sd=1) #beta = pm.Normal('beta', mu=0, sd=10, shape=2) beta = pm.Normal('beta', mu=0, sd=10) epsilon = pm.HalfCauchy('epsilon', 5) #mu = alpha + pm.math.dot(beta, X) mu = alpha + beta * X[0] y_pred = pm.Normal('y_pred', mu=mu, sd=epsilon, observed=y) trace_red = pm.sample(5000, njobs=1) pm.traceplot(trace_red) plt.figure() |
|
1 2 3 4 5 6 |
pm.summary(trace_red) mean sd mc_error hpd_2.5 hpd_97.5 n_eff Rhat alpha -0.09 0.10 8.34e-04 -0.29 0.10 14901.00 1.0 beta 0.95 0.09 7.39e-04 0.77 1.12 14187.41 1.0 epsilon 0.99 0.07 5.71e-04 0.86 1.13 13621.13 1.0 |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
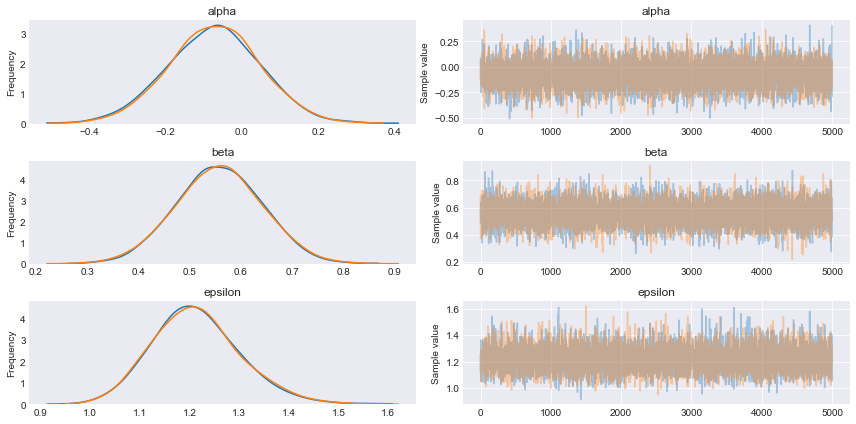
with pm.Model() as model_red: alpha = pm.Normal('alpha', mu=0, sd=1) #beta = pm.Normal('beta', mu=0, sd=10, shape=2) beta = pm.Normal('beta', mu=0, sd=10) epsilon = pm.HalfCauchy('epsilon', 5) #mu = alpha + pm.math.dot(beta, X) mu = alpha + beta * X[1] y_pred = pm.Normal('y_pred', mu=mu, sd=epsilon, observed=y) trace_red = pm.sample(5000, njobs=1) pm.traceplot(trace_red) plt.figure() |
|
1 2 3 4 5 6 |
pm.summary(trace_red) mean sd mc_error hpd_2.5 hpd_97.5 n_eff Rhat alpha -0.07 0.12 8.90e-04 -0.31 0.16 14302.06 1.0 beta 0.56 0.08 7.31e-04 0.40 0.72 14862.81 1.0 epsilon 1.21 0.09 6.83e-04 1.06 1.40 12632.99 1.0 |
|
1 2 3 4 5 6 7 |
x_2 = x_1 + np.random.normal(size=N, scale=0.01) y = x_1 + np.random.normal(size=N) X = np.vstack((x_1, x_2)) scatter_plot(X, y) plt.tight_layout() plt.figure() |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
with pm.Model() as model_red: alpha = pm.Normal('alpha', mu=0, sd=1) beta = pm.Normal('beta', mu=0, sd=10, shape=2) epsilon = pm.HalfCauchy('epsilon', 5) mu = alpha + pm.math.dot(beta, X) y_pred = pm.Normal('y_pred', mu=mu, sd=epsilon, observed=y) trace_red = pm.sample(5000, njobs=1) pm.traceplot(trace_red) plt.tight_layout() plt.figure() |
|
1 2 3 4 5 6 |
pm.summary(trace_red) mean sd mc_error hpd_2.5 hpd_97.5 n_eff Rhat alpha -0.07 0.12 8.90e-04 -0.31 0.16 14302.06 1.0 beta 0.56 0.08 7.31e-04 0.40 0.72 14862.81 1.0 epsilon 1.21 0.09 6.83e-04 1.06 1.40 12632.99 1.0 |
|
1 2 3 4 5 |
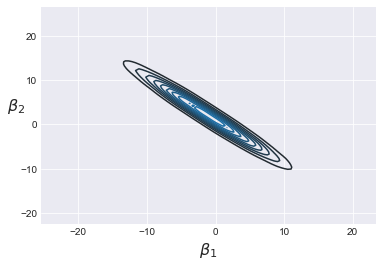
sns.kdeplot(trace_red['beta'][:,0], trace_red['beta'][:,1]) plt.xlabel(r'$\beta_1$', fontsize=16) plt.ylabel(r'$\beta_2$', fontsize=16, rotation=0) plt.figure() |
|
1 2 3 |
pm.forestplot(trace_red, varnames=['beta']) plt.figure() |
|
1 2 3 4 5 6 7 8 9 10 11 12 |
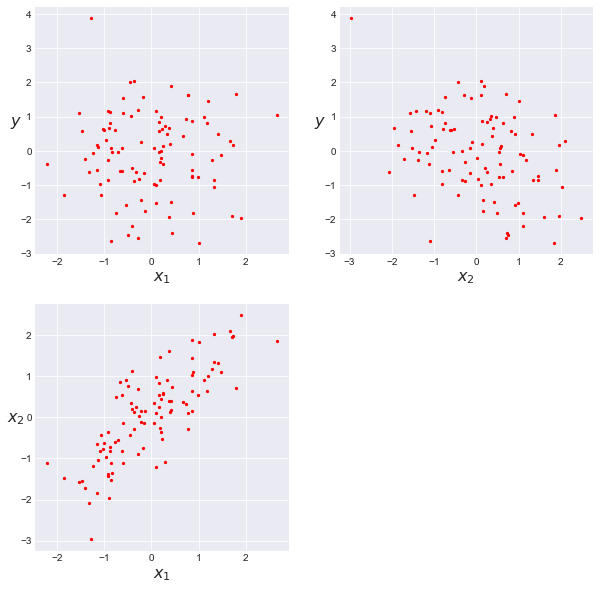
np.random.seed(314) N = 100 r = 0.8 x_1 = np.random.normal(size=N) x_2 = np.random.normal(loc=x_1 * r, scale=(1 - r ** 2) ** 0.5) y = np.random.normal(loc=x_1 - x_2) X = np.vstack((x_1, x_2)) scatter_plot(X, y) plt.figure() |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
with pm.Model() as model_ma: alpha = pm.Normal('alpha', mu=0, sd=10) beta = pm.Normal('beta', mu=0, sd=10, shape=2) epsilon = pm.HalfCauchy('epsilon', 5) mu = alpha + pm.math.dot(beta, X) y_pred = pm.Normal('y_pred', mu=mu, sd=epsilon, observed=y) trace_ma = pm.sample(5000, njobs=1) pm.traceplot(trace_ma) plt.figure() |
|
1 2 3 |
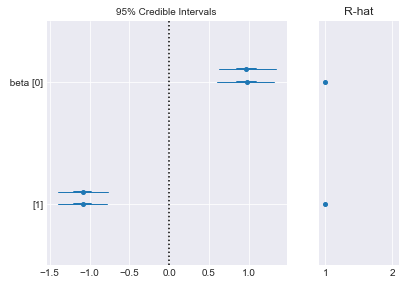
pm.forestplot(trace_ma, varnames=['beta']); plt.figure() |