Ref: Baysian Analysis with Python by Osvaldo Martin
—————————————————-
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 |
import pymc3 as pm import numpy as np import pandas as pd import scipy.stats as stats import matplotlib.pyplot as plt import seaborn as sns plt.style.use('seaborn-darkgrid') np.set_printoptions(precision=2) pd.set_option('display.precision', 2) np.random.seed(123) N = 100 alpha_real = 2.0 beta_real = [0.8, 1.6] eps_real = np.random.normal(0, 0.5, size=N) X = np.array([np.random.normal(i, j, N) for i,j in zip([8, 4], [2, 1])]) X_mean = X.mean(axis=1, keepdims=True) X_centered = X - X_mean y = alpha_real + np.dot(beta_real, X) + eps_real def scatter_plot(x, y): plt.figure(figsize=(10, 10)) for idx, x_i in enumerate(x): plt.subplot(2, 2, idx+1) plt.scatter(x_i, y, s=5, c="r") plt.xlabel('$x_{}$'.format(idx+1), fontsize=16) plt.ylabel('$y$', rotation=0, fontsize=16) plt.subplot(2, 2, idx+2) plt.scatter(x[0], x[1],s=5, c="r") plt.xlabel('$x_{}$'.format(idx), fontsize=16) plt.ylabel('$x_{}$'.format(idx+1), rotation=0, fontsize=16) scatter_plot(X, y) plt.figure() |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
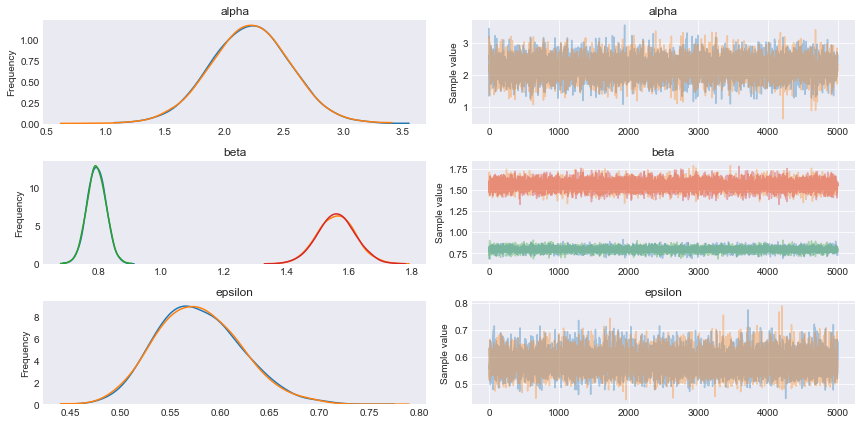
with pm.Model() as model_mlr: alpha_tmp = pm.Normal('alpha_tmp', mu=0, sd=10) beta = pm.Normal('beta', mu=0, sd=1, shape=2) epsilon = pm.HalfCauchy('epsilon', 5) mu = alpha_tmp + pm.math.dot(beta, X_centered) alpha = pm.Deterministic('alpha', alpha_tmp - pm.math.dot(beta, X_mean)) y_pred = pm.Normal('y_pred', mu=mu, sd=epsilon, observed=y) trace_mlr = pm.sample(5000, njobs=1) varnames = ['alpha', 'beta','epsilon'] pm.traceplot(trace_mlr, varnames) plt.figure() |
|
1 2 3 4 5 6 7 |
pm.summary(trace_mlr, varnames) mean sd mc_error hpd_2.5 hpd_97.5 n_eff Rhat alpha__0 2.22 0.33 3.25e-03 1.57 2.88 9801.47 1.0 beta__0 0.79 0.03 2.81e-04 0.74 0.85 10022.44 1.0 beta__1 1.56 0.06 6.41e-04 1.44 1.67 10201.08 1.0 epsilon 0.58 0.04 3.51e-04 0.50 0.67 12321.59 1.0 |