Ref: Baysian Analysis with Python by Osvaldo Martin
?????????????????-
階層ベイズによる直線回帰
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 |
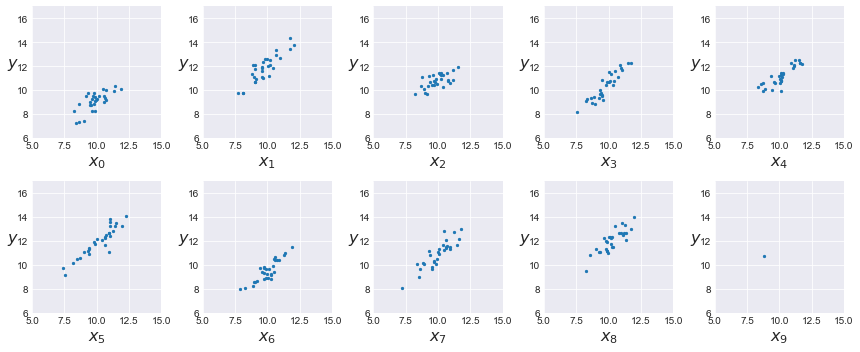
N = 30 M = 10 idx = np.repeat(range(M-1), N) idx = np.append(idx, 9) np.random.seed(123) alpha_real = np.random.normal(2, 0.5, size=M) beta_real = np.random.beta(6, 1, size=M) eps_real = np.random.normal(0, 0.5, size=len(idx)) y_m = np.zeros(len(idx)) x_m = np.random.normal(10, 1, len(idx)) y_m = alpha_real[idx] + beta_real[idx] * x_m + eps_real plt.figure(figsize=(12,5)) j, k = 0, N for i in range(M): plt.subplot(2,5,i+1) plt.scatter(x_m[j:k], y_m[j:k], s=5) plt.xlabel('$x_{}$'.format(i), fontsize=16) plt.ylabel('$y$', fontsize=16, rotation=0) plt.xlim(5, 15) plt.ylim(6, 17) j += N k += N plt.tight_layout() plt.figure() |
|
1 |
x_centered = x_m - x_m.mean() |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
with pm.Model() as unpooled_model: alpha_tmp = pm.Normal('alpha_tmp', mu=0, sd=10, shape=M) beta = pm.Normal('beta', mu=0, sd=10, shape=M) epsilon = pm.HalfCauchy('epsilon', 5) nu = pm.Exponential('nu', 1/30) y_pred = pm.StudentT('y_pred', mu= alpha_tmp[idx] + beta[idx] * x_centered, sd=epsilon, nu=nu, observed=y_m) alpha = pm.Deterministic('alpha', alpha_tmp - beta * x_m.mean()) start = pm.find_MAP() step = pm.NUTS(scaling=start) trace_up = pm.sample(2000, step=step, start=start, njobs=1) varnames=['alpha', 'beta', 'epsilon', 'nu'] pm.traceplot(trace_up, varnames) plt.figure() |
αの平均値μαの事前分布は、正規分布(μ_μα、σ_μα)
αの標準偏差σαの事前分布は、半コーシー分布(σ_σα)
βの平均値μβの事前分布は、正規分布(μ_μβ、σ_μβ)
βの標準偏差σβの事前分布は、半コーシー分布(σ_σβ)
αの事前分布は正規分布(μα,σα)
βの事前分布は正規分布(μβ,σβ)
μ= α + βx、
σの事前分布は、半コーシー分布
自由度λは、指数分布
y〜t分布(μ、σ、v)
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
with pm.Model() as hierarchical_model: alpha_tmp_mu = pm.Normal('alpha_tmp_mu', mu=0, sd=10) alpha_tmp_sd = pm.HalfNormal('alpha_tmp_sd', 10) beta_mu = pm.Normal('beta_mu', mu=0, sd=10) beta_sd = pm.HalfNormal('beta_sd', sd=10) alpha_tmp = pm.Normal('alpha_tmp', mu=alpha_tmp_mu, sd=alpha_tmp_sd, shape=M) beta = pm.Normal('beta', mu=beta_mu, sd=beta_sd, shape=M) epsilon = pm.HalfCauchy('epsilon', 5) nu = pm.Exponential('nu', 1/30) y_pred = pm.StudentT('y_pred', mu=alpha_tmp[idx] + beta[idx] * x_centered, sd=epsilon, nu=nu, observed=y_m) alpha = pm.Deterministic('alpha', alpha_tmp - beta * x_m.mean()) alpha_mu = pm.Deterministic('alpha_mu', alpha_tmp_mu - beta_mu * x_m.mean()) alpha_sd = pm.Deterministic('alpha_sd', alpha_tmp_sd - beta_mu * x_m.mean()) trace_hm = pm.sample(1000, njobs=1) varnames=['alpha', 'alpha_mu', 'alpha_sd', 'beta', 'beta_mu', 'beta_sd', 'epsilon', 'nu'] pm.traceplot(trace_hm, varnames) plt.figure() |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
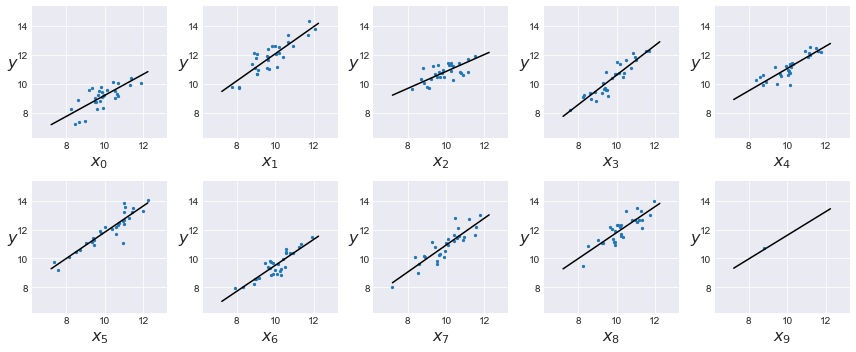
plt.figure(figsize=(12,5)) j, k = 0, N x_range = np.linspace(x_m.min(), x_m.max(), 10) for i in range(M): plt.subplot(2,5,i+1) plt.scatter(x_m[j:k], y_m[j:k], s=5) plt.xlabel('$x_{}$'.format(i), fontsize=16) plt.ylabel('$y$', fontsize=16, rotation=0) alfa_m = trace_hm['alpha'][:,i].mean() beta_m = trace_hm['beta'][:,i].mean() plt.plot(x_range, alfa_m + beta_m * x_range, c='k', label='y = {:.2f} + {:.2f} * x'.format(alfa_m, beta_m)) plt.xlim(x_m.min()-1, x_m.max()+1) plt.ylim(y_m.min()-1, y_m.max()+1) j += N k += N plt.tight_layout() plt.savefig('img421.png', dpi=300, figsize=(5.5, 5.5)) plt.figure() |