Ref: Baysian Analysis with Python by Osvaldo Martin
—————————————————-
正規分布から逸脱する外れ値が存在するときにt分布を用いたロバスト回帰推論:
アンスコムのquartetデータをIII(y3)を使用:
https://ja.wikipedia.org/wiki/アンスコムの例
アンスコムの数値例
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
I II III IV x y x y x y x y 10.0 8.04 10.0 9.14 10.0 7.46 8.0 6.58 8.0 6.95 8.0 8.14 8.0 6.77 8.0 5.76 13.0 7.58 13.0 8.74 13.0 12.74 8.0 7.71 9.0 8.81 9.0 8.77 9.0 7.11 8.0 8.84 11.0 8.33 11.0 9.26 11.0 7.81 8.0 8.47 14.0 9.96 14.0 8.10 14.0 8.84 8.0 7.04 6.0 7.24 6.0 6.13 6.0 6.08 8.0 5.25 4.0 4.26 4.0 3.10 4.0 5.39 19.0 12.50 12.0 10.84 12.0 9.13 12.0 8.15 8.0 5.56 7.0 4.82 7.0 7.26 7.0 6.42 8.0 7.91 5.0 5.68 5.0 4.74 5.0 5.73 8.0 6.89 |

Wikipediaには:
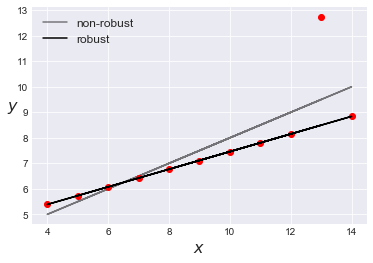
3番目のグラフ(左下)では、分布は線形であるが、回帰直線はその分布と異なっている。その違いは外れ値の存在に起因している。この外れ値の影響で回帰直線が変わり、相関係数は1から0.816に下がってしまっている。この場合はロバスト回帰が必要となる。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
ans = sns.load_dataset('anscombe') x_3 = ans[ans.dataset == 'III']['x'].values y_3 = ans[ans.dataset == 'III']['y'].values plt.figure(figsize=(10,5)) plt.subplot(1,2,1) beta_c, alpha_c = stats.linregress(x_3, y_3)[:2] plt.plot(x_3, (alpha_c + beta_c* x_3), 'k', label='y ={:.2f} + {:.2f} * x'.format(alpha_c, beta_c)) plt.plot(x_3, y_3, 'ro') plt.xlabel('$x$', fontsize=16) plt.ylabel('$y$', rotation=0, fontsize=16) plt.legend(loc=0, fontsize=14) plt.subplot(1,2,2) sns.kdeplot(y_3); plt.xlabel('$y$', fontsize=16) plt.tight_layout() plt.figure() |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 |
with pm.Model() as model_t: alpha = pm.Normal('alpha', mu=0, sd=100) beta = pm.Normal('beta', mu=0, sd=1) epsilon = pm.HalfCauchy('epsilon', 5) nu = pm.Deterministic('nu', pm.Exponential('nu_', 1/29) + 1) mu=alpha + beta * x_3 y_pred = pm.StudentT('y_pred', mu=mu, sd=epsilon, nu=nu, observed=y_3) rb = pm.Deterministic('rb', (beta * x_3.std() / y_3.std()) ** 2) y_mean = y_3.mean() ss_reg = pm.math.sum((mu - y_mean) ** 2) ss_tot = pm.math.sum((y_3 - y_mean) ** 2) rss = pm.Deterministic('rss', ss_reg/ss_tot) start = pm.find_MAP() step = pm.NUTS(scaling=start) trace_t = pm.sample(2000, step=step, start=start, njobs=1) beta_c, alpha_c = stats.linregress(x_3, y_3)[:2] plt.plot(x_3, (alpha_c + beta_c * x_3), 'k', label='non-robust', alpha=0.5) plt.plot(x_3, y_3, 'bo') alpha_m = trace_t['alpha'].mean() beta_m = trace_t['beta'].mean() plt.plot(x_3, alpha_m + beta_m * x_3, c='k', label='robust') plt.xlabel('$x$', fontsize=16) plt.ylabel('$y$', rotation=0, fontsize=16) plt.legend(loc=2, fontsize=12) plt.figure() |
|
1 |
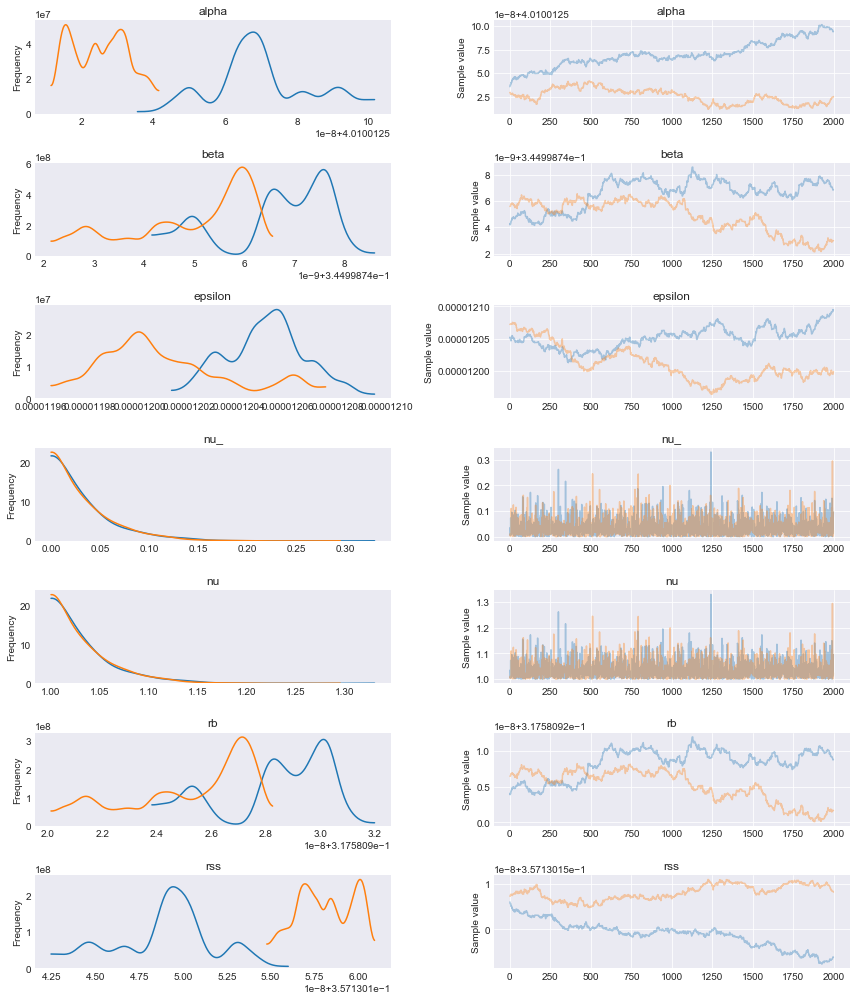
pm.traceplot(trace_t) |
|
1 2 |
varnames = ['alpha', 'beta', 'epsilon', 'nu_', 'nu', 'rb', 'rss'] pm.summary(trace_t, varnames) |
|
1 2 3 4 5 6 7 8 |
mean sd mc_error hpd_2.5 hpd_97.5 n_eff Rhat alpha 4.01e+00 2.50e-08 2.49e-09 4.01e+00 4.01e+00 1.21 2.99 beta 3.45e-01 1.45e-09 1.44e-10 3.45e-01 3.45e-01 2.73 1.45 epsilon 1.20e-05 2.98e-08 2.96e-09 1.20e-05 1.21e-05 2.01 1.64 nu_ 3.38e-02 3.35e-02 4.95e-04 9.04e-06 1.02e-01 3733.89 1.00 nu 1.03e+00 3.35e-02 4.95e-04 1.00e+00 1.10e+00 3733.89 1.00 rb 3.18e-01 2.67e-09 2.65e-10 3.18e-01 3.18e-01 2.73 1.45 rss 3.57e-01 5.14e-09 5.13e-10 3.57e-01 3.57e-01 1.22 2.99 |
|
1 2 3 4 5 6 7 |
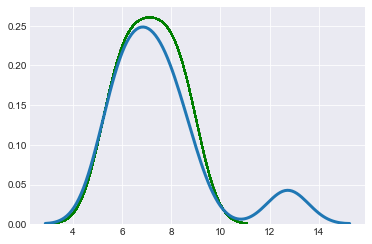
ppc = pm.sample_ppc(trace_t, samples=200, model=model_t, random_seed=2) for y_tilde in ppc['y_pred']: sns.kdeplot(y_tilde, alpha=0.5, c='g') sns.kdeplot(y_3, linewidth=3) plt.figure() |