Ref: Baysian Analysis with Python by Osvaldo Martin
—————————————————
ピアソンの総関係数の二乗である決定係数を2通りの方法で求める。
1つ目は、
rb = β*σ(x)/σ(y)
2つ目の方法は、最小二乗法
rss = ss_rss/ss_tot: ss_rss: フィットした直線とデータ平均値との分散
ss_tot: 予測変数の分散
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 |
np.random.seed(314) N = 100 alfa_real = 2.0 beta_real = 1.0 eps_real = np.random.normal(0, 0.5, size=N) x = np.random.normal(10, 1, N) y_real = alfa_real + beta_real * x y = y_real + eps_real with pm.Model() as model_n: alpha = pm.Normal('alpha', mu=0, sd=10) beta = pm.Normal('beta', mu=0, sd=1) epsilon = pm.HalfCauchy('epsilon', 5) mu = alpha + beta * x y_pred = pm.Normal('y_pred', mu=mu, sd=epsilon, observed=y) rb = pm.Deterministic('rb', (beta * x.std() / y.std()) ** 2) y_mean = y.mean() ss_reg = pm.math.sum((mu - y_mean) ** 2) ss_tot = pm.math.sum((y - y_mean) ** 2) rss = pm.Deterministic('rss', ss_reg/ss_tot) start = pm.find_MAP() step = pm.NUTS() trace_n = pm.sample(2000, step=step, start=start) pm.traceplot(trace_n) plt.figure() |
|
1 2 3 4 5 6 7 8 9 |
varnames = ['alpha', 'beta', 'epsilon', 'rb', 'rss'] pm.summary(trace_n, varnames) mean sd mc_error hpd_2.5 hpd_97.5 n_eff Rhat alpha 1.26 0.44 1.21e-02 0.43 2.11 1185.17 1.0 beta 1.07 0.04 1.19e-03 0.99 1.15 1169.39 1.0 epsilon 0.47 0.03 6.93e-04 0.41 0.54 1858.94 1.0 rb 0.86 0.07 1.90e-03 0.73 0.99 1186.37 1.0 rss 0.86 0.07 1.90e-03 0.73 0.99 1183.43 1.0 |
σ_x1を2、σ_x2を1か3として、相関係数-0.8. -0.5, 0, 0.5, 0.8の5つにおいて、2変量正規分布を描く:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
sigma_x1 = 2 sigmas_x2 = [1, 3] rhos = [-0.8, -0.5, 0, 0.5, 0.8] x, y = np.mgrid[-6:6:.1, -6:6:.1] pos = np.empty(x.shape + (2,)) pos[:, :, 0] = x; pos[:, :, 1] = y f, ax = plt.subplots(len(sigmas_x2), len(rhos), sharex=True, sharey=True) for i in range(2): for j in range(5): sigma_x2 = sigmas_x2[i] rho = rhos[j] cov = [[sigma_x1**2, sigma_x1*sigma_x2*rho], [sigma_x1*sigma_x2*rho, sigma_x2**2]] rv = stats.multivariate_normal([0, 0], cov) ax[i,j].contour(x, y, rv.pdf(pos)) ax[i,j].plot(0, 0, label="$\\sigma_{{x2}}$ = {:3.2f}\n$\\rho$ = {:3.2f}".format(sigma_x2, rho), alpha=0) ax[i,j].legend() ax[1,2].set_xlabel('$x_1$') ax[1,0].set_ylabel('$x_2$') plt.figure() |
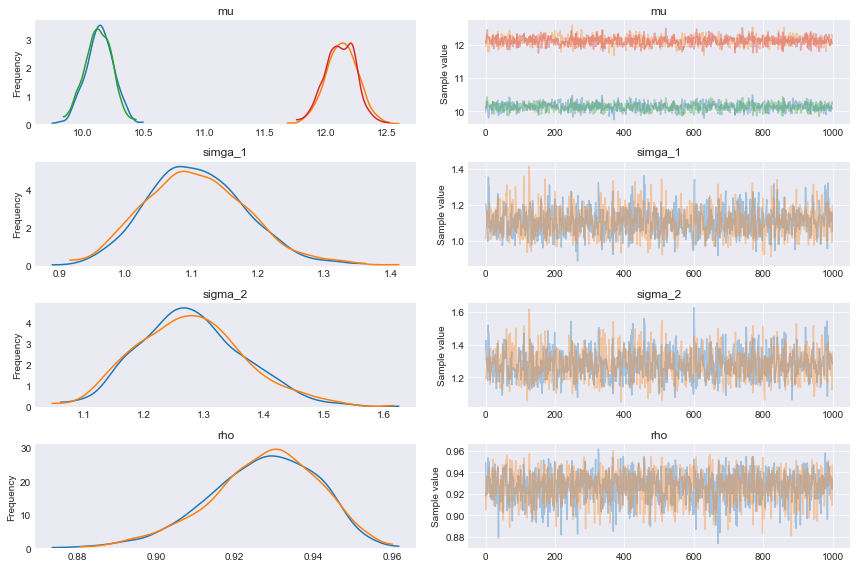
2つの分布、平均、偏差に対する相関係数KDEを求める。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 |
np.random.seed(314) N = 100 alfa_real = 2.0 beta_real = 1.0 eps_real = np.random.normal(0, 0.5, size=N) x = np.random.normal(10, 1, N) y_real = alfa_real + beta_real * x y = y_real + eps_real data = np.stack((x, y)).T with pm.Model() as pearson_model: mu = pm.Normal('mu', mu=data.mean(0), sd=10, shape=2) sigma_1 = pm.HalfNormal('simga_1', 10) sigma_2 = pm.HalfNormal('sigma_2', 10) rho = pm.Uniform('rho', -1, 1) cov = pm.math.stack(([sigma_1**2, sigma_1*sigma_2*rho], [sigma_1*sigma_2*rho, sigma_2**2])) y_pred = pm.MvNormal('y_pred', mu=mu, cov=cov, observed=data) start = pm.find_MAP() step = pm.NUTS(scaling=start) trace_p = pm.sample(1000, step=step, start=start, njobs=1) pm.traceplot(trace_p) plt.figure() |