Ref: Baysian Analysis with Python by Osvaldo Martin
—————————
線形回帰モデルを、最小二乗法と比較して、Baysianによるものを比較して理解すれば、ベイズの特徴がよく分かる。
—————————
一次線形回帰式:y = α + βx
—————————
と表されるが、確率論では、
—————————
y 〜 N(μ=α + βx, σ=ε):つまりデータyは、平均値μ=α + βx, 標準偏差σ=εの正規分布に従うとする。
—————————
なるほど、実際のデータでは、誤差によるばらつきが発生するわけで、ばらつきを含めて平均値μは、正規分布であろうと置くわけだ。
まずは、既知の正規分布に基づく誤差εのデータを作成して、それをサンプルデータの誤差変動として加えたほぼ正規分布する人工サンプルデータを作成し、それをモデルに当てはめ、既知の分布に近いものがモデルから得られるか確かめてみる。αを2.0、βを1.0、正規分布は平均値0,標準偏差0.5、サンプル数N=100、乱数はseed()で固定すると、以下のように記述できる。
|
1 2 3 4 5 |
np.random.seed(314) N = 100 alfa_real = 2.0 beta_real = 1.0 eps_real = np.random.normal(0, 0.5, size=N) |
次に、平均値10、標準偏差1、サンプル数N=100で正規分布乱数を発生させて、誤差εをデータばらつきとして加えて、人工サンプルデータとする。
|
1 2 3 |
x = np.random.normal(10, 1, N) y_real = alfa_real + beta_real * x y = y_real + eps_real |
生成したデータの性状と、誤差を含まない場合の一次線形回帰式:y = α + βxをグラフ表示する。
|
1 2 3 4 5 6 7 8 9 10 11 |
plt.figure(figsize=(5, 7.5)) plt.subplot(2, 1, 1) plt.plot(x, y, 'r.') plt.xlabel('$x$', fontsize=12) plt.ylabel('$y$', fontsize=12, rotation=0) plt.plot(x, y_real, 'b') plt.subplot(2, 1, 2) sns.kdeplot(y) plt.xlabel('$y$', fontsize=12) plt.figure() |
次に一次線形回帰式:y = α + βxのベイズモデルy 〜 N(μ=α + βx, σ=ε)を作成する。
ベイズモデルとして各パラメータの事前分布として、αは平均値0、標準偏差10の正規分布、βは平均値0、標準偏差1の正規分布、誤差εは半コーシー分布とする。
※コーシー分布の関数の基本形は次式のようにあらわされる.

ここで, α(>0)、μはそれぞれ定数であり, とくにμはコーシー分布の最頻値(確率密度関数f(x)が最大になるxの値)である。
コーシー分布の特徴
? 時々とんでもない外れ値を出すことがある分布
? 実現値の場合,裾の方に必ず出現度数がある=裾が重い分布。
? べき分布の一種 ? 大数の法則が成立しない
らしい。
|
1 2 3 4 5 6 7 8 9 10 11 |
with pm.Model() as model: alpha = pm.Normal('alpha', mu=0, sd=10) beta = pm.Normal('beta', mu=0, sd=1) epsilon = pm.HalfCauchy('epsilon', 5) mu = pm.Deterministic('mu', alpha + beta * x) y_pred = pm.Normal('y_pred', mu=mu, sd=epsilon, observed=y) start = pm.find_MAP() step = pm.Metropolis() trace = pm.sample(11000, step, start, njobs=1) |
各パラメータをメトロポリス法でトレースすると
|
1 2 3 4 |
trace_n = trace[1000:] pm.traceplot(trace_n) plt.figure() |

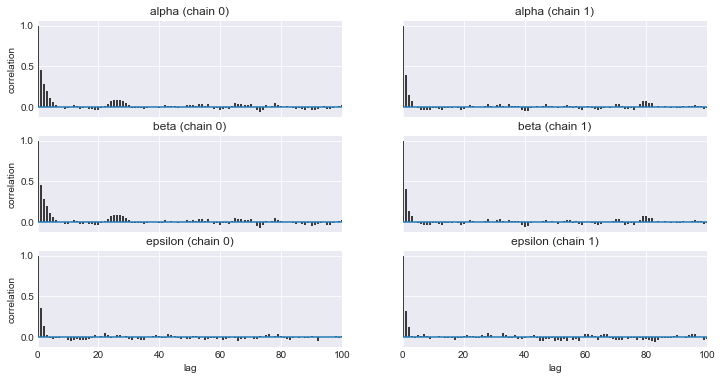
αとβは、トレースプロットでは、上下変動して収束していない。εは良さそうで、μは、α、βから決定されるので、Deterministicとなっているが、分布図は小さな分布の集合体として描かれることが面白い。
α、βが収束しないので、自己相関プロットをとる。
|
1 2 3 4 5 6 7 8 9 10 11 |
varnames = ['alpha', 'beta', 'epsilon'] pm.autocorrplot(trace_n, varnames) plt.savefig('img405.png', dpi=300, figsize=(5.5, 5.5)) plt.figure() sns.kdeplot(trace_n['alpha'], trace_n['beta']) plt.xlabel(r'$\alpha$', fontsize=16) plt.ylabel(r'$\beta$', fontsize=16, rotation=0) plt.figure() |
|
1 2 3 4 5 6 7 8 9 10 11 |
varnames = ['alpha', 'beta', 'epsilon'] pm.autocorrplot(trace_n, varnames) plt.savefig('img405.png', dpi=300, figsize=(5.5, 5.5)) plt.figure() sns.kdeplot(trace_n['alpha'], trace_n['epsilon']) plt.xlabel(r'$\alpha$', fontsize=16) plt.ylabel(r'$\epsilon$', fontsize=16, rotation=0) plt.figure() |
|
1 2 3 4 5 6 7 8 9 10 |
varnames = ['alpha', 'beta', 'epsilon'] pm.autocorrplot(trace_n, varnames) plt.savefig('img405.png', dpi=300, figsize=(5.5, 5.5)) plt.figure() sns.kdeplot(trace_n['beta'], trace_n['epsilon']) plt.xlabel(r'$\beta$', fontsize=16) plt.ylabel(r'$\epsilon$', fontsize=16, rotation=0) plt.figure() |
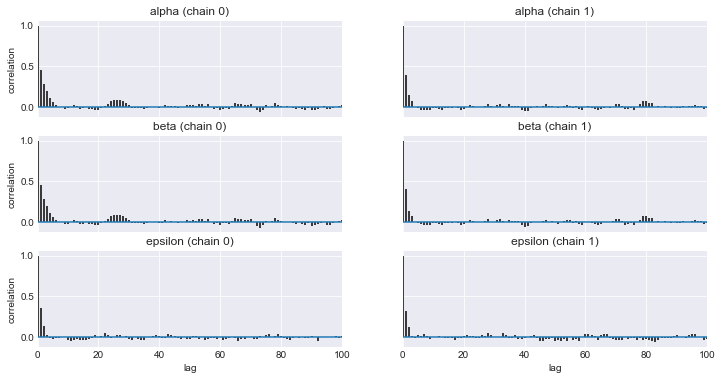

なるほど、αとβだけが、直線関係の相関があることが理解できた。
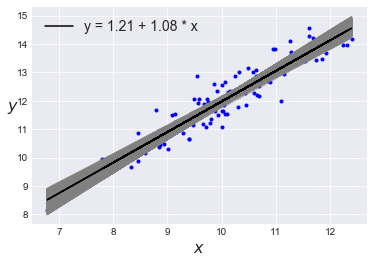
次にα、βの分布の平均値を用いて、モデルから当てはめられたy = α_m + β_m*xを、人工サンプルデータのx値と描いてみると、
|
1 2 3 4 5 6 7 8 9 |
plt.plot(x, y, 'b.'); alpha_m = trace_n['alpha'].mean() beta_m = trace_n['beta'].mean() plt.plot(x, alpha_m + beta_m * x, c='k', label='y = {:.2f} + {:.2f} * x'.format(alpha_m, beta_m)) plt.xlabel('$x$', fontsize=16) plt.ylabel('$y$', fontsize=16, rotation=0) plt.legend(loc=2, fontsize=14) plt.figure() |
y= 1.21 + 1.08 * x となった。もともとの人工サンプルデータはy = 2.0 + 1.0 * xで作成したので、α値は少し低めとなった。
分布の不確実性を考慮して、図を描くと、
|
1 2 3 |
len(trace_n['alpha']) 20000 |
で、
|
1 2 3 4 5 6 7 8 9 10 |
plt.plot(x, y, 'b.'); idx = range(0, len(trace_n['alpha']), 10) plt.plot(x, trace_n['alpha'][idx] + trace_n['beta'][idx] * x[:,np.newaxis], c='gray', alpha=0.5); plt.plot(x, alpha_m + beta_m * x, c='k', label='y = {:.2f} + {:.2f} * x'.format(alpha_m, beta_m)) plt.xlabel('$x$', fontsize=16) plt.ylabel('$y$', fontsize=16, rotation=0) plt.legend(loc=2, fontsize=14) plt.figure() |
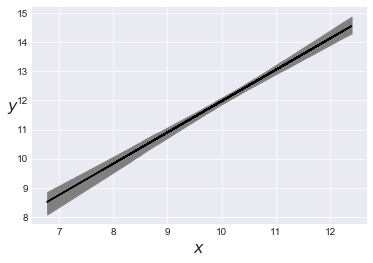
最高事後密度信用区間(HPD区間)を加えると、
|
1 2 3 4 5 6 7 8 9 10 11 |
plt.plot(x, alpha_m + beta_m * x, c='k', label='y = {:.2f} + {:.2f} * x'.format(alpha_m, beta_m)) idx = np.argsort(x) x_ord = x[idx] sig = pm.hpd(trace_n['mu'], alpha=.02)[idx] plt.fill_between(x_ord, sig[:,0], sig[:,1], color='gray') plt.xlabel('$x$', fontsize=16) plt.ylabel('$y$', fontsize=16, rotation=0) plt.figure() |
argsort(): np.argsortは、ソート結果の配列のインデックスを返す。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
ppc = pm.sample_ppc(trace_n, samples=1000, model=model) plt.plot(x, y, 'b.') plt.plot(x, alpha_m + beta_m * x, c='k', label='y = {:.2f} + {:.2f} * x'.format(alpha_m, beta_m)) sig0 = pm.hpd(ppc['y_pred'], alpha=0.5)[idx] sig1 = pm.hpd(ppc['y_pred'], alpha=0.05)[idx] plt.fill_between(x_ord, sig0[:,0], sig0[:,1], color='gray', alpha=1) plt.fill_between(x_ord, sig1[:,0], sig1[:,1], color='gray', alpha=0.5) plt.xlabel('$x$', fontsize=16) plt.ylabel('$y$', fontsize=16, rotation=0) plt.figure() |