Ref: Baysian Analysis with Python by Osvaldo Martin
—————————————————–
Matlibplotのグラフの見栄えを良くするSeabornをインポート。
NumpyとPandasの小数点以下表示を2桁に指定しておく。
|
1 2 3 4 5 6 7 8 9 |
import matplotlib.pyplot as plt import numpy as np from scipy import stats import seaborn as sns import pymc3 as pm import pandas as pd plt.style.use('seaborn-darkgrid') np.set_printoptions(precision=2) pd.set_option('display.precision', 2) |
正規分布に基づいたBaysian Model：
事前分布として、平均値μには、区間[l, h]を持つ一様分布
μ〜Uniform(l, h)
標準偏差σについては、半正規分布
σ〜HalfNormal(σσ)
尤度は正規分布を用いる。
y〜Normal(μ, σ)
平均値40, 標準偏差5で、正規分布するランダム値を48個含む配列を作成する。
|
1 2 3 4 5 6 |
from numpy.random import * list = [] for i in range(48): list.append(normal(40,5)) list |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 |
[38.00378924619505, 42.06013750097147, 49.226279915590176, 40.420736068494584, 36.21510258802349, 38.10801326130363, 40.248259948871905, 35.491474634814516, 39.76009281135123, 37.327747745690225, 40.2309735769475, 37.84870980048326, 46.40237862124653, 50.20752284041242, 43.08270051638168, 46.272586543790965, 37.86430869950899, 34.16777444255556, 44.51368036654519, 47.529092878933156, 39.17104730241858, 42.52921885463609, 45.61446676135757, 39.71851853940985, 27.498524060331622, 35.93441323260724, 38.372754611614695, 37.19973151414081, 42.35586608308128, 40.26704464461231, 31.031374744583765, 37.923176800648314, 38.726626661988945, 43.35041456670035, 45.34847276004376, 40.37064193521784, 51.03064132861753, 40.15363260173313, 46.15177898309288, 31.660307609511158, 38.215200860686394, 37.80333387683497, 36.80683937128298, 39.779440116720764, 33.3740398683643, 38.66316846720863, 46.66476025455213, 37.2674879958202] |
上記のモデルに沿って、事前分布が、平均値が一様分布、標準偏差が正規分布、尤度がランダム作成した正規分布値、
事後分布が正規分布であるベイズモデルを作成する
|
1 2 3 4 5 6 7 8 9 10 11 |
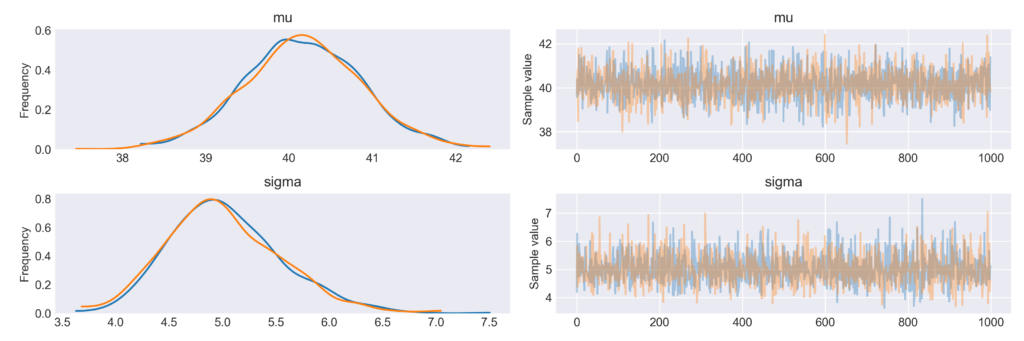
with pm.Model() as model_g: mu = pm.Uniform('mu', 20, 60) sigma = pm.HalfNormal('sigma', sd=5) y = pm.Normal('y', mu=mu, sd=sigma, observed=list) trace_g = pm.sample(1100, njobs=1) chain_g = trace_g[100:] pm.traceplot(chain_g) plt.savefig('img_list.png', dpi=300, figsize=(5.5, 5.5)) plt.figure() |
で、M−H法で事後分布のサンプリングを行うと：
|
1 2 3 4 5 6 |
Auto-assigning NUTS sampler... Initializing NUTS using jitter+adapt_diag... Sequential sampling (2 chains in 1 job) NUTS: [sigma, mu] 100%|??????????| 1600/1600 [00:01<00:00, 1506.61it/s] 100%|??????????| 1600/1600 [00:01<00:00, 1247.52it/s] |
|
1 2 |
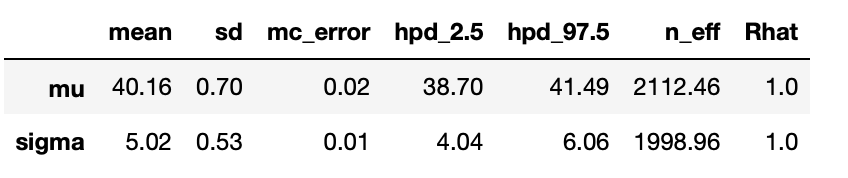
df = pm.summary(chain_g) df |
事後分布から48ｘ20個の予測データ・セットを生成する。
|
1 2 3 4 5 6 7 8 9 10 |
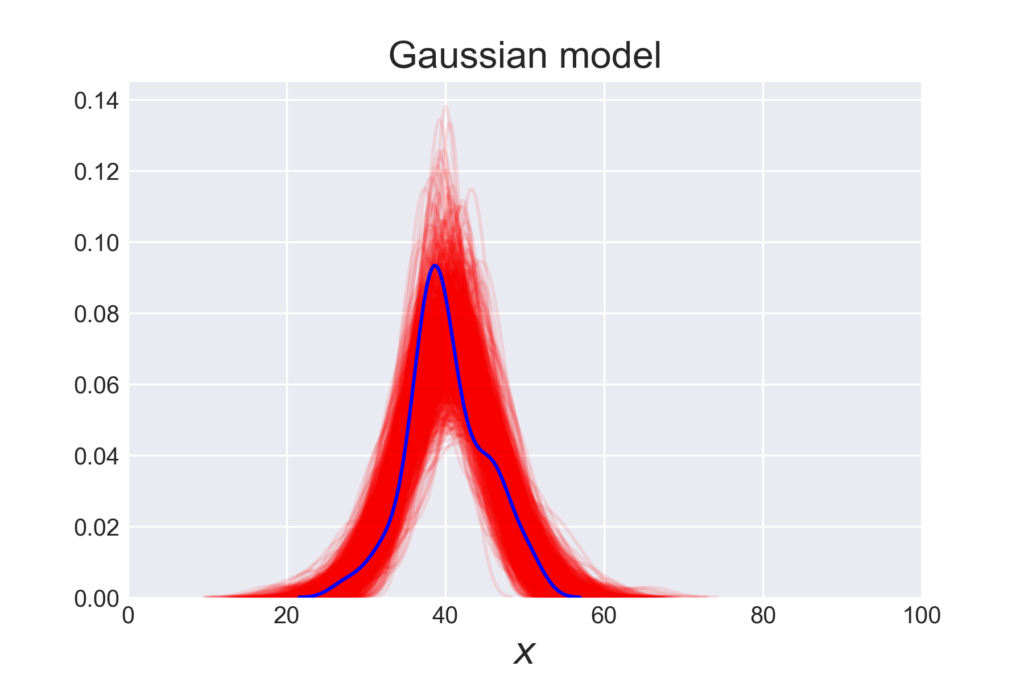
y_pred = pm.sample_posterior_predictive(chain_g, 20, model_g, size=len(data)) for i in y_pred['y'].reshape(960,48): sns.kdeplot(i, color='r', alpha=0.1) sns.kdeplot(list, color='b') plt.xlim(0, 100) plt.title('Gaussian model', fontsize=16) plt.xlabel('$x$', fontsize=16) plt.savefig('img_list3.png', dpi=300, figsize=(5.5, 5.5)) plt.figure() |
ブルーの線はKDE、赤色線は、事後予測サンプル
