Ref: Baysian Analysis with Python by Osvaldo Martin
———————————-
Bernoulli trial:Coin-flipping 5回の施行でコインの表が出る確率を40%としたとき、Scipyをimportして、
|
1 2 3 4 5 6 |
import scipy.stats as stats n_experiments = 5 theta_real = 0.4 data = stats.bernoulli.rvs(p=theta_real, size=n_experiments) print(data) |
outputの一例は、
|
1 |
[1 0 0 1 0] |
outputを繰り返すと、
|
1 |
[1 0 1 1 0] |
となったりもする。そこで乱数を固定して、出力も一定とする。
|
1 2 3 4 5 6 7 8 9 |
import scipy.stats as stats np.random.seed(123) n_experiments = 5 theta_real = 0.4 data = stats.bernoulli.rvs(p=theta_real, size=n_experiments) print(data) [1 0 0 0 1] |
Bernoulli trialのBayes Modelは、
事前分布をβ関数:
θ 〜 Beta(α, β)
尤度を二項分布:
y 〜 Bin(n=5, p=θ)
とすれば、事後分布〜y・θ
PyMC3をインポートして、
|
1 2 3 4 5 |
import pymc3 as pm with pm.Model() as bernoulli_model: theta = pm.Beta('theta', alpha=1, beta=1) y = pm.Bernoulli('y', p=theta, observed=data) |
と表せる。PyMC3は、Theanoを利用して、PythonコードをC++に変換するため、高速演算が可能である。
次に、最大事後確率を初期値、find_MAP()で求めて、Metropolis-Hesting法をサンプリング法として指定し、サンプル数1000を指定して、トレース変数へ収める。
|
1 2 3 4 5 6 7 8 9 |
import pymc3 as pm with pm.Model() as bernoulli_model: theta = pm.Beta('theta', alpha=1, beta=1) y = pm.Bernoulli('y', p=theta, observed=data) start = pm.find_MAP() step = pm.Metropolis() trace = pm.sample(1000, step=step, start=start) |
Burn-inを100として、θをトレースする。
|
1 2 3 4 |
burnin = 100 chain = trace[burnin:] pm.traceplot(chain, lines={'theta':theta_real}); plt.savefig('img_Bernoulli.png', dpi=300, figsize=(5.5, 5.5)) |
|
1 2 3 4 5 |
logp = -3.4657, ||grad|| = 0.5: 100%|??????????| 6/6 [00:00<00:00, 690.53it/s] Multiprocess sampling (2 chains in 2 jobs) Metropolis: [theta] Sampling 2 chains: 100%|??????????| 3000/3000 [00:00<00:00, 6317.60draws/s] The number of effective samples is smaller than 25% for some parameters. |
2 chain実行されたようで、
左 KDE:カーネル密度推定(実際のθ=0.4をライン表示)と、右:M−H法でのサンプリングの過程は以下の通り。

|
1 2 3 4 5 6 7 8 |
with bernoulli_model: step = pm.Metropolis() multi_trace = pm.sample(1000, step=step, njobs=4) burnin = 100 multi_chain = multi_trace[burnin:] pm.traceplot(multi_chain, lines={'theta':theta_real}); plt.savefig('img_Bernoulli2.png', dpi=300, figsize=(5.5, 5.5)) |
|
1 2 3 |
Multiprocess sampling (4 chains in 4 jobs) Metropolis: [theta] Sampling 4 chains: 100%|??????????| 6000/6000 [00:01<00:00, 4096.80draws/s] |
|
1 |
pm.summary(multi_chain) |
|
1 |
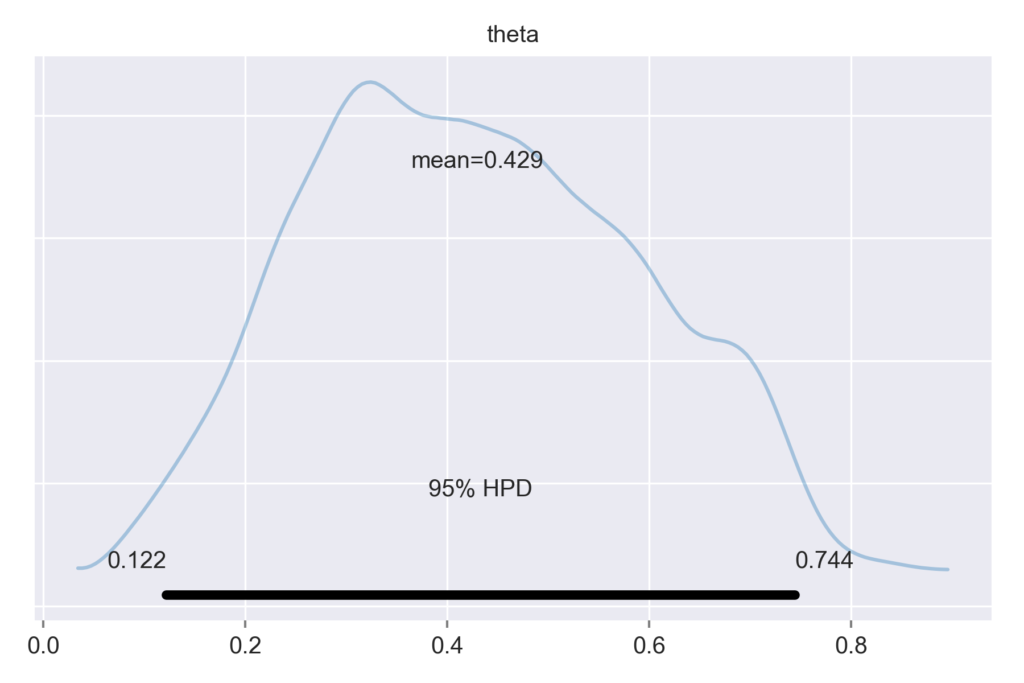
pm.plot_posterior(chain, kde_plot=True) |
|
1 |
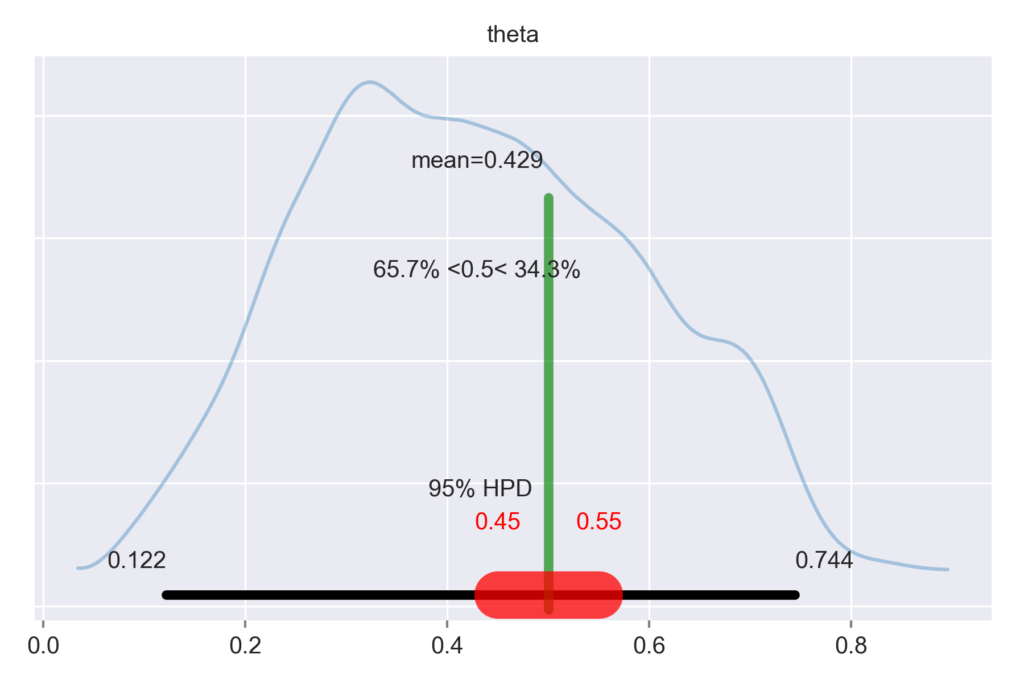
pm.plot_posterior(chain, kde_plot=True, rope=[0.45,.55], ref_val=0.5) |