Bayesian Biostatistics by E Lesaffre & AB Lawson, Chapter 4 学習ノート
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
何箇所か意識を失いながら、前半部分を読んで概略を理解した。もう一度、振り返ってみる。
胆石を有する患者における総胆管結石の発生を予測する後ろ向き研究65名の血清アルカリフォスファターゼ(alkaline phosphatase, alp)のデータ65個と、前向きに行った健常人250名分の血清アルカリフォスファターゼ(alkaline phosphatase, alp)のデータ250個が、ALP.txtのデータ構造 315個のデータが収納されている。
テキストデータファイルALP.txtをベクトル変数ALPにロードして、attach()関数で、データアクセス時にいちいち”ALP$”を付けなくても、データアクセスできるようにする。
|
1 2 |
> ALP = read.delim("ALP.txt", header=TRUE) > attach(ALP) |
artikel=0が250個、artikel=1が65個。はじめのプログラムでは、alkfos[artikel==0]で前向き研究のデータartikel=0の250件を取り出している。残りのartikel=1の65個のデータは事前に行った後ろ向き研究のデータであり、後のプログラムで事前情報として使用する。
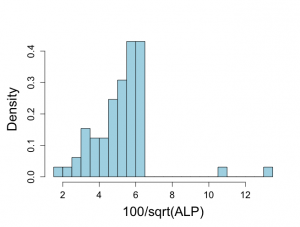
始めのプログラムでは、250個のalpデータを事前情報なしに分析することを試みている。
結果として3次元プロットが描かれる。
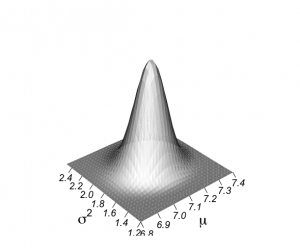
この3次元プロットwireframe()関数の実行には、以下の命令でlatticeパッケージを取り込んで使用している。
|
1 2 |
install.packages("lattice") library(lattice) |
lattice には S 用に開発されたグラフィックスパラダイム Trellis の R への移植関数が入っている.例えば,三次元散布図は,関数 cloud() や関数 wireframe() で描くことが出来る。
http://cse.naro.affrc.go.jp/takezawa/r-tips/r/58.html
|
1 2 |
> data(volcano) > wireframe(volcano, shade = TRUE, aspect = c(61/87, 0.4), light.source = c(10,0,10)) |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 |
> objects(2) [1] "alkfos" "artikel" > > alp <- alkfos[artikel==0] > talp <- 100*alp^(-1/2) > nalp <- length(alp) > > mtalp <- mean(talp) > vartalp <- var(talp) > sdtalp <- sqrt(var(talp)) > ntalp <- length(talp) > > mtalp;sdtalp [1] 7.108724 [1] 1.365344 > > par(mfrow=c(1,1)) > par(pty="m") > par(mar=c(5,5,4,2)+0.1) > > # histogram of transformed response, graph is not included in book > > hist(talp,xlab="100/sqrt(ALP)",nclas=30,col="light blue", + cex.lab=1.8,cex.axis=1.3,prob=T,main="") > > # graph of 2-dimensional normal posterior distribution > > unl.mu <- 6.8 > upl.mu <- 7.4 > > unl.sigma2 <- 1.2 > upl.sigma2 <- 2.5 > > # log posterior of mu and sigma2 given y: graph! > > # choice of 200 for calculations, 50 for plotting > > nmu <- 30 > nsigma2 <- 30 > > mugrid <- expand.grid(mu=do.breaks(c(unl.mu,upl.mu),nmu), + sigma2=do.breaks(c(unl.sigma2,upl.sigma2),nsigma2)) > > mugrid$mu [1] 6.80 6.82 6.84 6.86 6.88 6.90 6.92 6.94 6.96 6.98 7.00 7.02 7.04 7.06 7.08 7.10 [17] 7.12 7.14 7.16 7.18 7.20 7.22 7.24 7.26 7.28 7.30 7.32 7.34 7.36 7.38 7.40 6.80 ....... [945] 7.08 7.10 7.12 7.14 7.16 7.18 7.20 7.22 7.24 7.26 7.28 7.30 7.32 7.34 7.36 7.38 [961] 7.40 > mugrid$sigma2 [1] 1.200000 1.200000 1.200000 1.200000 1.200000 1.200000 1.200000 1.200000 1.200000 [10] 1.200000 1.200000 1.200000 1.200000 1.200000 1.200000 1.200000 1.200000 1.200000 [19] 1.200000 1.200000 1.200000 1.200000 1.200000 1.200000 1.200000 1.200000 1.200000 ....... [955] 2.500000 2.500000 2.500000 2.500000 2.500000 2.500000 2.500000 > > logpropposter <- -(ntalp+2)*log(mugrid$sigma2)/2 > logpropposter <- logpropposter -0.5*mugrid$sigma2^(-1)*((ntalp-1)*vartalp+ntalp*(mtalp-mugrid$mu)^2) > propposter <- exp(logpropposter-max(logpropposter)) > > par(mfrow=c(1,1)) > par(pty="m") > par(mar=c(6,4,4,2)) > trellis.par.set("axis.line",list(col="transparent")) > wireframe(propposter ~ mugrid$mu*mugrid$sigma2,outer=TRUE, + shade=TRUE,bty="l",zlab="", + xlab=list(label=expression(paste(mu)),font=1,cex=1.8), + ylab=list(label=expression(paste(sigma^{2})),font=1,cex=1.8), + scales = list(arrows=FALSE, cex= 1.2, col = "black",font = 3, + z = list(draw = FALSE)), + par.box = list(col=NA), + shade.colors = function(irr, ref, height, w = 1) + grey(w * irr + (1 - w) * (1 - (1 - ref)^0.4)),zoom=1) |
サンプルデータの作成に関数 expand.grid()を以下のように使用している。
|
1 2 |
> mugrid <- expand.grid(mu=do.breaks(c(unl.mu,upl.mu),nmu), + sigma2=do.breaks(c(unl.sigma2,upl.sigma2),nsigma2)) |
expand.grid()の中身を見てみる。
mu=do.breaks(c(unl.mu,upl.mu),nmu),
sigma2=do.breaks(c(unl.sigma2,upl.sigma2),nsigma2)
変数を実際の数字に置き換えてみると、
mu=do.breaks(c(6.8,7.4),30),
sigma2=do.breaks(c(1.2,2.5),30)
|
1 2 3 4 5 6 7 8 9 10 |
> mu=do.breaks(c(6.8,7.4),30) > mu [1] 6.80 6.82 6.84 6.86 6.88 6.90 6.92 6.94 6.96 6.98 7.00 7.02 7.04 7.06 7.08 7.10 [17] 7.12 7.14 7.16 7.18 7.20 7.22 7.24 7.26 7.28 7.30 7.32 7.34 7.36 7.38 7.40 > sigma2=do.breaks(c(1.2,2.5),30) > sigma2 [1] 1.200000 1.243333 1.286667 1.330000 1.373333 1.416667 1.460000 1.503333 1.546667 [10] 1.590000 1.633333 1.676667 1.720000 1.763333 1.806667 1.850000 1.893333 1.936667 [19] 1.980000 2.023333 2.066667 2.110000 2.153333 2.196667 2.240000 2.283333 2.326667 [28] 2.370000 2.413333 2.456667 2.500000 |
つまり、平均値μと、分散σ^2を30分割して、それぞれ31個の数値を作成し、
それをもとにexpand.grid(mu, sigma2)で31?31=961個の組み合わせデータを発生させて変数mugridに収めている。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
> mugrid mu sigma2 1 6.80 1.200000 2 6.82 1.200000 3 6.84 1.200000 .... 31 7.40 1.200000 32 6.80 1.243333 33 6.82 1.243333 .... 62 7.40 1.243333 63 6.80 1.286667 64 6.82 1.286667 65 6.84 1.286667 66 6.86 1.286667 .... 500 6.86 1.893333 [ reached getOption("max.print") -- 461 行を無視しました ] |
生成した961個の組み合わせは、μとσ^2に関する事前の知識が無い場合、無情報同時事前分布を
p(μ,σ^2) ∝ σ^-2
として、これを正規分布N(μ,σ^2)からのデータとしての尤度L(μ,σ^2|y)
L(μ,σ^2|y)= 1/(2πσ^2)^(2/n) * exp(-1/2σ^2 * [[(n – 1)*s^2 + n*(y_mean – μ)^2]]
をかけ合わせて、解析的に求められる事後分布関数
p(μ,σ^2|y)∝ 1/(σ^(n+2) * exp(-1/2σ^2 * [(n – 1)*s^2 + n*(y_mean – μ)^2])
に以下の命令ではめ込んでいく。
ただし計算にはlogを利用して、
log(p(μ,σ^2|y)) ∝ log [1/(σ^(n+2) * exp(-1/2σ^2 * [(n – 1)*s^2 + n*(y_mean – μ)^2])]
= log [1/(σ^(n+2))] + log[exp(-1/2σ^2 * [(n – 1)*s^2 + n*(y_mean – μ)^2])]]
= log [1/(σ^(n+2))] + [-1/2σ^2 * [(n – 1)*s^2 + n*(y_mean – μ)^2]]
= -(n+2)*log[σ] + [0.5 * σ^-2 * [(n – 1)*s^2 + n(y_mean – μ)^2]
ここでσ^2 = mugrid$sigma2、n = ntalp、s = vartalpなので、
log(p(μ,σ^2|y)) ∝ -(ntalp+2)*log(mugrid$sigma2)/2 – 0.5*mugrid$sigma2^(-1)*((ntalp-1)*vartalp+ntalp*(mtalp-mugrid$mu)^2)
最後にlogをexp()で元に戻すと、
propposter = exp(log(p(μ,σ^2|y))) = exp(-(ntalp+2)*log(mugrid$sigma2)/2 – 0.5*mugrid$sigma2^(-1)*((ntalp-1)*vartalp+ntalp*(mtalp-mugrid$mu)^2))
と事後分布が解析的に求まる。
|
1 2 3 |
> logpropposter <- -(ntalp+2)*log(mugrid$sigma2)/2 > logpropposter <- logpropposter -0.5*mugrid$sigma2^(-1)*((ntalp-1)*vartalp+ntalp*(mtalp-mugrid$mu)^2) > propposter <- exp(logpropposter-max(logpropposter)) |
これによりベクトル変数propposterには、μとσ^2の組み合わせ931個に対応する931個の事後分布予測観測値データp(y|μ, σ^2)が、無情報事前分布σ^-2と尤度関数L(μ,σ^2|y)との積として収められる。
|
1 2 3 4 5 6 |
> propposter [1] 7.333516e-11 2.546073e-10 8.132766e-10 2.390091e-09 6.462484e-09 1.607657e-08 [7] 3.679560e-08 7.748315e-08 1.501162e-07 2.675817e-07 4.388279e-07 6.621261e-07 ....... [955] 1.132830e-03 7.883342e-04 5.270891e-04 3.385992e-04 2.089854e-04 1.239294e-04 [961] 7.060913e-05 |
3次元立体図の作成にはwireframe()関数を用いて作成される。
wireframe()関数のパラメータの骨格は、
wireframe(z ~ x * y)
であり、ここでは、
wireframe(propposter ~ mu * sigma2)
として作図されている。
|
1 2 3 4 5 6 7 8 9 |
> wireframe(propposter ~ mugrid$mu*mugrid$sigma2,outer=TRUE, + shade=TRUE,bty="l",zlab="", + xlab=list(label=expression(paste(mu)),font=1,cex=1.8), + ylab=list(label=expression(paste(sigma^{2})),font=1,cex=1.8), + scales = list(arrows=FALSE, cex= 1.2, col = "black",font = 3, + z = list(draw = FALSE)), + par.box = list(col=NA), + shade.colors = function(irr, ref, height, w = 1) + grey(w * irr + (1 - w) * (1 - (1 - ref)^0.4)),zoom=1) |
以上が、μとσ^2に関する事前情報がない場合、無情報事前分布としてσ^-2を用いた場合に、正規分布にとして解析的に計算できる尤度関数L(μ,σ^2|y)をかけ合わせた
p(μ,σ^2|y) ∝ L(μ,σ^2|y) * σ^-2
を用いて事後分布を推測したベイズ流の解析が示された。
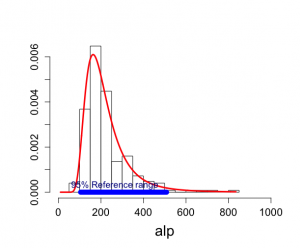
古典的頻度流アプローチでは、alpの250のデータに対して、生データに対しては、平均223.9、分散11049、標準偏差105
95%参照区間はy_mean±1.96σ√(1+1/n)を用いて [104.33, 510.18]となった。
|
1 2 3 4 5 6 7 |
> hist(alp) > mean(alp) [1] 223.852 > var(alp) [1] 11049.13 > sd(alp) [1] 105.1148 |
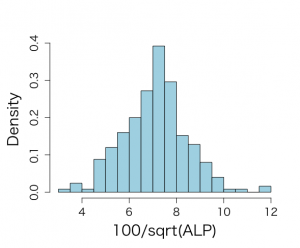
あるいは、100*√alpとすると、その平均7.11、分散1.86、標準偏差1.37
95%参照区間はy_mean±1.96σ√(1+1/n)を用いて [4.43, 9.79]となった。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
> talp <- 100*alp^(-1/2) > nalp <- length(alp) > > mtalp <- mean(talp) > vartalp <- var(talp) > sdtalp <- sqrt(var(talp)) > ntalp <- length(talp) > > mtalp;sdtalp [1] 7.108724 [1] 1.365344 > nalp [1] 250 > ntalp [1] 250 > vartalp [1] 1.864165 > hist(alp) > hist(alp, breaks=100) |
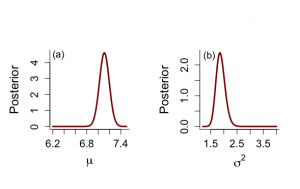
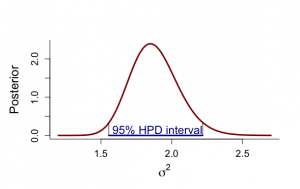
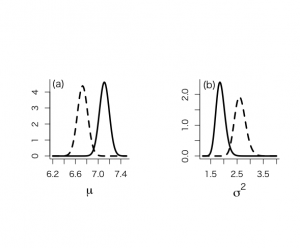
一方、ベイズ流では、μの事後分布は7.11と変わらないが、μ自身の分散は0.0075、標準偏差0.087で、μ自身の95%HPD信用区間は[6.94, 7.28]で、σ^2の平均値は1.88であり、その分散は0.029、標準偏差0.17で、95%HPD信用区間は[1.56, 2.22]で、これらの結果から得られる観測値の事後分布は解析的にはt249(7.11, 1.37)分布となり、予測観測値の95%信用区間(健常人正常値)は[104.1, 513.2]となる。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 |
> alp <- alkfos[artikel==0] > talp <- 100*alp^(-1/2) > nalp <- length(alp) > > mtalp <- mean(talp) > vartalp <- var(talp) > sdtalp <- sqrt(var(talp)) > ntalp <- length(talp) > > mtalp;sdtalp [1] 7.108724 [1] 1.365344 > > par(mfrow=c(1,1)) > par(pty="m") > par(mar=c(5,5,4,2)+0.1) > > > # marginal posterior distribution of MEAN & SIGMAイ > # Figure 4.2 but only part of ninf prior > > > unl.mu <- 6.2 > upl.mu <- 7.5 > > unl.sigma2 <- 1.2 > upl.sigma2 <- 4 > > nmu <- 100 > nsigma2 <- 100 > > # values using ni prior > > mu <- seq(unl.mu,upl.mu,length=nmu) > mus <- (mu-mtalp)/(sdtalp/sqrt(ntalp)) > pmu <- dt(mus,ntalp-1)*sqrt(ntalp)/sdtalp > sigma2 <- seq(unl.sigma2,upl.sigma2,length=nsigma2) > sigma2s <- (ntalp-1)*vartalp/sigma2 > psigma2 <- dchisq(sigma2s,ntalp-1)*(ntalp-1)*vartalp/(sigma2^2) > > > par(mfrow=c(1,2)) > par(pty="s") > > plot(mu,pmu,type="n",xlab=expression(paste(mu)),ylab="Posterior", + ylim=c(0,max(pmu)),bty="l",main="",cex.lab=1.5,cex.axis=1.3) > lines(mu,pmu,lwd=3,col="dark red") > text(6.3,4.5,"(a)",cex=1.2) > > plot(sigma2,psigma2,type="n",xlab=expression(paste(sigma^{2})), + ylab="Posterior",ylim=c(0,max(psigma2)),bty="l",main="",cex.lab=1.5, + cex.axis=1.3) > lines(sigma2,psigma2,lwd=3,col="dark red") > text(1.45,2.3,"(b)",cex=1.2) > > # summary statistics from ninf prior > > # for mu > > mupostmean <- mtalp > mupostvar <- (ntalp-1)*vartalp/(ntalp*(ntalp-3)) > mu.post.unl <- mupostmean - qt(0.975,ntalp-1)*sdtalp/sqrt(ntalp) > mu.post.upl <- mupostmean + qt(0.975,ntalp-1)*sdtalp/sqrt(ntalp) > mupostmean;mupostvar;mu.post.unl;mu.post.upl [1] 7.108724 [1] 0.007517036 [1] 6.93865 [1] 7.278797 > > # for sigma^2 > > sigma2postmean <- vartalp*(ntalp-1)/(ntalp-3) > sigma2postmode <- vartalp*(ntalp-1)/(ntalp+1) > sigma2postmedian <- vartalp*(ntalp-1)/qchisq(0.5,ntalp-1) > sigma2postvar <- vartalp^2*2*(ntalp-1)^2/((ntalp-3)^2*(ntalp-5)) > sigma2.post.unl <- (ntalp-1)*vartalp/qchisq(0.975,ntalp-1) > sigma2.post.upl <- (ntalp-1)*vartalp/qchisq(0.025,ntalp-1) > sigma2postmean;sigma2postmode;sigma2postmedian;sigma2postvar;sigma2.post.unl;sigma2.post.upl [1] 1.879259 [1] 1.849311 [1] 1.869167 [1] 0.02882951 [1] 1.575613 [1] 2.240392 > > > # function to calculate hpd for sigmaイ > > unl.sigma2 <- 1.2 > upl.sigma2 <- 2.7 > nsigma2 <- 300 > sigma2 <- seq(unl.sigma2,upl.sigma2,length=nsigma2) > sigma2s <- (ntalp-1)*vartalp/sigma2 > psigma2 <- dchisq(sigma2s,ntalp-1)*(ntalp-1)*vartalp/(sigma2^2) > > a <- 1 > #h <- 20 > min <- 1 > max <- 1 > minimum <- 9999 > eps <- 0.001 > > for (a in 1:(nsigma2-1)){ + begin <- sigma2[a] + for (h in (a+1):nsigma2){ + #print(a);print(h) + end <- sigma2[h] + diffunction <- abs(psigma2[a]-psigma2[h]) + cumprobbegin <- pchisq(vartalp*(ntalp-1)/sigma2[a], ntalp-1) + cumprobend <- pchisq(vartalp*(ntalp-1)/sigma2[h], ntalp-1) + difcum <- cumprobbegin-cumprobend + if((abs(difcum-0.95) < eps) && (diffunction < minimum)) {minimum <- diffunction; min <- a; max <- h} + } + } > > min;max;minimum [1] 72 [1] 204 [1] 0.007943811 > sigma2[min];sigma2[max] [1] 1.556187 [1] 2.218395 > > par(mfrow=c(1,1)) > par(pty="m") > > plot(sigma2,psigma2,type="n",xlab=expression(paste(sigma^{2})), + ylab="Posterior",ylim=c(0,max(psigma2)),bty="l",main="",cex.lab=1.5, + cex.axis=1.2) > lines(sigma2,psigma2,lwd=3,col="dark red") > segments(sigma2[min],0,sigma2[min],psigma2[min]) > segments(sigma2[max],0,sigma2[max],psigma2[max]) > segments(sigma2[min],0,sigma2[max],0,col="dark blue",lwd=3) > text(1.9,0.15,"95% HPD interval",col="dark blue",cex=1.4) > > # PPD > > sdppd <- sdtalp*sqrt(1+1/ntalp) > ppd.unl <- mtalp-qt(0.975,ntalp-1)*sdppd > ppd.upl <- mtalp+qt(0.975,ntalp-1)*sdppd > ppd.unl;ppd.upl;100^2/ppd.unl^2;100^2/ppd.upl^2 [1] 4.414255 [1] 9.803192 [1] 513.1982 [1] 104.0555 |
頻度統計流とベイズ統計流(無情報事前分布)を比較すると、
|
1 2 3 4 5 |
平均値μ 分散σ^2 標準偏差σ 95%参照区間 alp値 頻度統計流 7.11 1.86 1.37 [4.43, 9.79] [104.33, 510.18] ベイズ統計流 7.11±0.0087 1.88±0.17 1.37±0.41 * [104.1, 513.2] 95%HPD信用区間 [6.94, 7.28] [1.56, 2.22] |
次のプロジェクトでは、ALP.txtに含まれている65件の後ろ向き研究のデータを事前分布情報として利用することを示している。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
# SAMPLING FROM PRODUCT OF INFORMATIVE PRIORS, using Method of Composition attach(ALP) objects(2) # historical data calculate Ninvchイ alphis <- alkfos[artikel==1] talp0 <- 100*alphis^(-1/2) mtalp0 <- mean(talp0) vartalp0 <- var(talp0) sdtalp0 <- sqrt(var(talp0)) ntalp0 <- length(talp0) mtalp0;sdtalp0;ntalp0 par(mfrow=c(1,1)) par(pty="m") # histogram of transformed response, graph is not included in book hist(talp0,xlab="100/sqrt(ALP)",nclas=30,col="light blue", cex.lab=1.8,cex.axis=1.3,prob=T,main="") |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 |
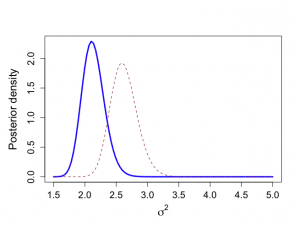
> # We use historical data to calculate prior values > > mu0 <- mtalp0 > sigma20 <- vartalp0/ntalp0 > nu0 <- ntalp0-1 > tau20 <- vartalp0 > kappa0 <- ntalp0 > > > mu0;sigma20;nu0;tau20 [1] 5.24849 [1] 0.0423147 [1] 64 [1] 2.750455 > > # Data from prospective study with 250 individuals (current study) > > alp <- alkfos[artikel==0] > talp <- 100*alp^(-1/2) > > mtalp <- mean(talp) > vartalp <- var(talp) > sdtalp <- sqrt(var(talp)) > ntalp <- length(talp) > > mtalp;vartalp;sdtalp;ntalp [1] 7.108724 [1] 1.864165 [1] 1.365344 [1] 250 > > # Start the sampling procedure via Method of Composition > # First sample sigma^2, then mu > # For sigma^2 we need a trick since posterior is known up to a constant > # We use here SIR based on an approximating scale inv-chisqd distribution > > unl.mu <- 6.2 > upl.mu <- 7.4 > > unl.sigma2 <- 1.5 > upl.sigma2 <- 5 > > > nmu <- 100 > nsigma2 <- 100 > ntilde <- 100 > > sigma2 <- seq(unl.sigma2,upl.sigma2,length=nsigma2) > gridsize <- sigma2[2]-sigma2[1] > mubar <- (mu0/sigma20+ntalp*mtalp/sigma2)/(1/sigma20+ntalp/sigma2) > taubar2 <- 1/(1/sigma20+ntalp/sigma2) > > sigma2s <- nu0*tau20/sigma2 > psigma2 <- dchisq(sigma2s,nu0)*nu0*tau20/(sigma2^2) > > loglastfact <- rep(0,nsigma2) > > for (i in 1:ntalp){ + loglastfact <- loglastfact + log(dnorm(talp[i],mean=mubar,sd=sqrt(sigma2))) + } > loglastfact <- loglastfact - min(loglastfact) > lastfact <- exp(loglastfact) > > psigma2bar <- sqrt(taubar2)*dnorm(mubar,mean=mu0,sd=sqrt(sigma20))*psigma2*lastfact > totalarea <- sum(psigma2bar)*gridsize > spsigma2bar <- psigma2bar/totalarea > > > # Distribution from joint conjugate prior, serves as a comparison > > mubarj <- (kappa0*mu0+ntalp*mtalp)/(kappa0+ntalp) > kappabarj <- kappa0+ntalp > nubarj <- nu0 + ntalp > taubarp1j <- nu0*tau20 > taubarp2j <- (ntalp-1)*vartalp > taubarp3j <- (mtalp-mu0)^2*kappa0*ntalp/(kappa0+ntalp) > taubar2j <- (taubarp1j+taubarp2j+taubarp3j)/nubarj > > sigma2sj <- nubarj*taubar2j/sigma2 > psigma2conjugate <- dchisq(sigma2sj,nubarj)*nubarj*taubar2j/(sigma2^2) > > > # Approximating inv chisq distribution, to be used in SIR sampling later on > > moment1sigma2bar <- spsigma2bar%*%sigma2*gridsize > moment2sigma2bar <- spsigma2bar%*%sigma2^2*gridsize > varsigma2bar <- moment2sigma2bar-moment1sigma2bar^2 > a <- moment1sigma2bar > b <- varsigma2bar > df <- 2*a^2/b+4 > s2 <- (df-2)*a/df > > sigma2s <- df*s2/sigma2 > psigma2approx <- dchisq(sigma2s,df)*df*s2/(sigma2^2) > > # Graphs not shown in book to compare > # p(sigma^2| y) as given by expression (4.19) in book: spsigma2bar > # Conjugate prior based on equivalent information: psigma2conjugate > # Approximate scaled inverse chi^2 distribution: psigma2approx > > par(mar=c(5,5,4,2)+0.1) > > > plot(sigma2,spsigma2bar,xlab=expression(sigma^{2}),ylab="Posterior density", + type="n", main="",cex.lab=1.5,cex.axis=1.3) > lines(sigma2,spsigma2bar,lwd=3,col="blue") > lines(sigma2,psigma2conjugate,lty=2,col="dark red") > lines(sigma2,psigma2approx,lty=4,col="purple") |
|
1 2 3 4 5 6 7 8 9 |
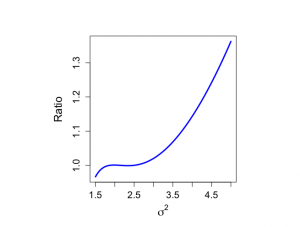
> # Evaluate (4.19) with approximation > > par(pty="s") > > plot(sigma2,spsigma2bar/psigma2approx,xlab=expression(sigma^{2}), + ylab="Ratio", + type="n", main="",cex.lab=1.5,cex.axis=1.3) > lines(sigma2,spsigma2bar/psigma2approx,lwd=3,col="blue") > |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 |
> # Weighted resampling (SIR) method > # We sample from approximating scaled inv-chisqd distribution, then resample > > NSIMUL <- 10000 > nsimul <- 1000 > > set.seed(777) > > phi.u <- rchisq(NSIMUL,df) > theta.u <- 1/phi.u > sigma2.1 <- df*s2*theta.u > nsigma2 <- 100 > sigma2 <- seq(unl.sigma2,upl.sigma2,length=nsigma2) > sigma2s <- df*s2/sigma2 > psigma2approx <- dchisq(sigma2s,df)*df*s2/(sigma2^2) > > # Histogram of sample of sigma^2 from approximate scaled inverse-chi^2 distribution > > hist(sigma2.1,prob=T,xlab=expression(sigma^{2}), + ylab="",main="",cex.lab=1.5,col="light blue", + cex.axis=1.3) > lines(sigma2,psigma2approx,lwd=3) > > > mubar.u <- (mu0/sigma20+ntalp*mtalp/sigma2.1)/(1/sigma20+ntalp/sigma2.1) > taubar2.u <- 1/(1/sigma20+ntalp/sigma2.1) > > sigma2s.u <- nu0*tau20/sigma2.1 > psigma2.u <- dchisq(sigma2s.u,nu0)*nu0*tau20/(sigma2.1^2) > > loglastfact.u <- rep(0, NSIMUL) > > for (i in 1:ntalp){ + loglastfact.u <- loglastfact.u + log(dnorm(talp[i],mean=mubar.u,sd=sqrt(sigma2.1))) + } > loglastfact.u <- loglastfact.u - min(loglastfact.u) > lastfact.u <- exp(loglastfact.u) > > post2 <- sqrt(taubar2.u)*dnorm(mubar.u,mean=mu0,sd=sqrt(sigma20))*psigma2.u*lastfact.u > > sigma2sappr.u <- df*s2/sigma2.1 > post1 <- dchisq(sigma2sappr.u,df)*df*s2/(sigma2.1^2) > v <- post2/post1 > w <- v/sum(v) |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 |
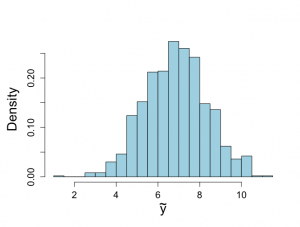
> # Now resample > > sigma2.2 <- sample(sigma2.1, size=nsimul, replace=F, prob=w) > > # Figure 4.4, obtained from Method of Composition > > par(mfrow=c(1,2)) > par(pty="s") > > > hist(sigma2.2,prob=T,xlab=expression(sigma^{2}), + ylab="",main="",cex.lab=1.5,col="light blue",ylim=c(0,2.2),xlim=c(1.5,3), + cex.axis=1.3) > lines(sigma2,spsigma2bar,lwd=3) > lines(sigma2,psigma2conjugate,lty=4) > text(1.6,2.2,"(a)",cex=1.2) > > > pmean <- mean(sigma2.2) > pmedian <- median(sigma2.2) > pvar <- var(sigma2.2) > quantile(sigma2.2,c(0.025,0.975)) 2.5% 97.5% 1.814895 2.530581 > unl.conf <- pmean -1.96*sqrt(pvar)/sqrt(length(sigma2.2)) > upl.conf <- pmean +1.96*sqrt(pvar)/sqrt(length(sigma2.2)) > pmean;pmedian;pvar;unl.conf;upl.conf [1] 2.13937 [1] 2.128304 [1] 0.03331027 [1] 2.128058 [1] 2.150682 > > > #Now sample mu > > > mubar.2 <- (mu0/sigma20+ntalp*mtalp/sigma2.2)/(1/sigma20+ntalp/sigma2.2) > sigma2bar.2 <- 1/(1/sigma20+ntalp/sigma2.2) > > mu.2 <- rnorm(nsimul,mean=mubar.2, sd=sqrt(sigma2bar.2)) > > hist(mu.2,xlab=expression(mu),prob=T, + ylab="",main="",cex.lab=1.5,col="light blue",ylim=c(0,4.5),xlim=c(6.5,7.1), + cex.axis=1.3) > text(6.53,4.5,"(b)",cex=1.2) > > # Compare with posterior obtained from conjugate > > muj <- seq(unl.mu,upl.mu,length=nmu) > musj <- (muj-mubarj)/(sqrt(taubar2j)/sqrt(kappabarj)) > pmuj <- dt(musj,nubarj)*sqrt(kappabarj)/sqrt(taubar2j) > > lines(muj,pmuj,lty=4) > > pmean <- mean(mu.2) > pmedian <- median(mu.2) > pvar <- var(mu.2) > quantile(mu.2,c(0.025,0.975)) 2.5% 97.5% 6.625876 6.965635 > unl.conf <- pmean -1.96*sqrt(pvar)/sqrt(length(mu.2)) > upl.conf <- pmean +1.96*sqrt(pvar)/sqrt(length(mu.2)) > pmean;pmedian;pvar;unl.conf;upl.conf [1] 6.799245 [1] 6.797344 [1] 0.00753436 [1] 6.793865 [1] 6.804625 > > > # Sample from ppd, figure not shown in book > > par(mfrow=c(1,1)) > par(pty="m") > > future.u <- rnorm(nsimul,mu.2,sqrt(sigma2.2)) > > hist(future.u,xlab=expression(tilde(y)),nclas=30,col="light blue", + cex.lab=1.8,cex.axis=1.3,prob=T,main="") > > > mean(future.u) [1] 6.859368 > > qfuturey <- quantile(future.u,c(0.025,0.975)) > qfutureALT <- 100^2/qfuturey^2 > > qfuturey;qfutureALT 2.5% 97.5% 4.047415 9.790413 2.5% 97.5% 610.4420 104.3273 |
過去のデータは、解析的に事前分布N−Inv−χ^2(μ0:事前平均,k0:事前情報サンプルサイズ,v0:σ^2の事前平均,σ0^2)を、尤度関数L(μ,σ^2|y)をかけ合わせて、事後分布N−Inv−χ^2(μ_bar, k_bar, v_bar, σ_bar^2)となり、
解析的に、
μ_bar = (k0*μ0 + n* y_bar) / (k0 + n)
k_bar = k0 + n
v_bar = v0 + n
vσ_bar^2 = v0σ0^2 + (n-1)s^2 + k0n/(k0 + n)*(y_bar – μ0)^2
で求まる。
周辺事後分布の導出も以下のように決定される。
p(μ|σ^2, y) = N(μ|μ_bar, σ^2/k_bar)
p(μ|y) = tv_bar(μ|μ_bar, σ_bar^2/k_bar)
p(σ^2|y) = Inv-χ2(σ^2|v_bar, σ_bar^2)
共役事前分布はN-Inv-χ^2(5.25, 65, 64, 2.76)
事後分布はN-Inv-χ^2(6.72, 315, 314, 2.61)
事後平均6.72は、事前平均5.25と標本平均7.11の重み付き平均である。μの事後分散は0.0083、標準偏差0.0083であり、以前の無情報事前分布から求めた事後分散0.0075より大きい。
μの95%信用区間は[6.54, 6.90]
σ^2の事後平均は2.62で、事後分散は0.044、標準偏差0.21、95%信用区間は[2.24, 3.07]で、95%HPD区間[2.23, 3.04]
将来の観測値の分布はt314(6.72, 1.62)分布であり、yの95%信用区間は[3.54, 9.91]で、対応するalp 95%正常範囲は[101.9, 796.7]である。
|
1 2 3 4 5 6 7 8 |
平均値μ 分散σ^2 標準偏差σ 95%参照区間 alp値 頻度統計流 7.11 1.86 1.37 [4.43, 9.79] [104.33, 510.18] ベイズ統計流[無情報] 7.11±0.0087 1.88±0.17 1.37±0.41 [4.41,9.80] [104.1, 513.2] 95%HPD信用区間 [6.94, 7.28] [1.56, 2.22] ベイズ統計流[事前情報] 6.72±0.0091 2.62±0.21 1.50±0.46 [3.54, 9.91] [101.9, 796.7] 95%HPD信用区間 [6.54, 6.90] [2.23, 3.04] |
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
ベイズ流とは何か?
古典的な頻度統計では、現在のデータ(例えば健常人250名のアルカリフォスファターゼのデータ)から、95%の健常人が含まれるであろう正常値範囲を推測する場合、母分散は正規分布に従うという極限定理(あるいは信念)に基いて、平均値および分散からN(平均値,分散)をモデルとして、95%参照区間をμ±1.96σ√(1+1/n)で求める。
ベイズ統計流では、例えば正規分布の要素である平均値や分散自体が、推定上は一定の分布範囲を持ち、平均値の平均±√分散、分散の平均±√分散となる。従って、それらパラメータ自体の分布を考慮にいれた観測予測値は、頻度統計論で固定化された平均や分散で算出された95%参照区間よりも広い幅を持ったものとなる。
加えて、ベイズ流では、得られた観測データは、何らかの事前分布に乗じられる尤度として用いられ、観測後の予測事後分布データは、事後分布=観測データ尤度?事前分布となる。
事前分布として何も情報がない場合、無情報事前分布として、一様分布等が選択される。正規分布では観測データの[分散^-2]等、一様分布が一般的に用いられ、その場合、事後分布は尤度関数がそのまま反映されることとなる。何らかの事前情報がデータとして利用できる場合、解析的に尤度関数、事前分布、事後分布を求めるためには、共役分布を利用して求める。事前情報が利用できると、観測データから得られる尤度関数の分布密度は、事前分布に引っ張られて、新たな事後分布を生む。
しかしながら、この方法では、共役性のある関数モデルに当てはめないと、解析的に求めることはできないので、複雑なモデルでは不可能となる。
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
この章の言いたいことは、ベイズ的な得られたデータの位置付け、モデルとしてのパラメータや、事後分布から推測される信用区間に対する考え方が主で、加えて解析的に共役関数を利用して求める方法には限界があるということを理解するということであろう。
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー