Bayesian Biostatistics by E Lesaffre & AB Lawson, Chapter 5 学習ノート
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
とにかく一旦、理解できるかどうかにかかわらず全体を走り読みして、次にRプログラム動かして、その詳細部分の理解から入るようにする。
本章は、ベイズの根幹に関わる事前分布について、深い考察を記述している。
ベイズに歴史的に敵対的な統計学者が、この事前分布情報の取扱に含まれる主観情報の問題点を攻撃し続けたようだ。そこで、ベイズ論者は、以下に事前分布を正論化するかについて、たいへんな努力を積み重ねてきたようである。とくに、事前情報が「ほとんど無い」場合、無情報事前分布なる考えから、フィッシャーの統計情報量の平方根から算出されるjeffreysの事前分布の考え方、弱情報/漠然事前分布等への考え、情報がある場合にも、専門家による知識を取り入れる方法や、圧倒的な事前情報を元に設計する場合など、事前分布の選択一つに相当なうんちくがあることが理解できる(ただし、詳しい内容は難解でわからない)。面白いのは、第?相臨床試験において、通常、事前情報たる第一相や第二相のデータを組み込むことは、頻度論では認められてこなかったが、ベイズ流では当然、利用できる情報があるのならば、それらを適正に加味することが当然であろうとの考えであるが、一方で、どのように組み込むかについては、懐疑的な立場や熱狂的な立場など、それはそれで複雑そうであるということがなんとなく感じられた。
5.1 はじめに
三種類の事前分布
1) 共役事前分布
2) 無情報事前分布
3) 情報あり事前分布
5.2 ベイズの定理の逐次利用
5.3 共役事前分布
5.3.1 1変量分布
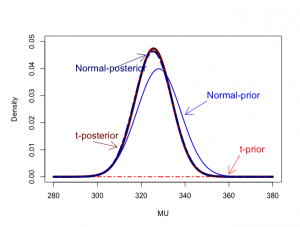
例V.2:食事研究:正規事前分布とt事前分布
食事研究がどういうものであったか振り返ると、IBBENS調査がベルギー銀行員に対して行われた事前調査で371名の男性と192名の女性、合わせて563名のコレステロール値で、その後のIBBENS-2調査はベルギーで行われた仮想のコレステロール値調査。
|
1 2 3 4 5 6 7 |
> #NORMAL versus t-prior > > mumin <-280 > mumax <-380 > priormu <-328 > priorvar <- 100 > mu <- seq(mumin,mumax,(mumax-mumin)/200) |
IBBENS調査では、563名の標本平均は328 mg/dayで、標本標準偏差は120.3 mg/day
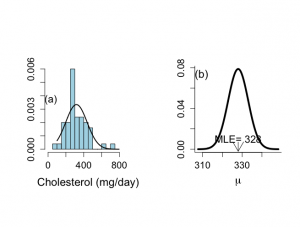
muには、280〜380までの範囲において200刻みで数値が収められた。
事前分布として、正規分布を選択の場合は、N(328,100)を選択できる
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
> mu [1] 280.0 280.5 281.0 281.5 282.0 282.5 283.0 283.5 284.0 284.5 285.0 285.5 [13] 286.0 286.5 287.0 287.5 288.0 288.5 289.0 289.5 290.0 290.5 291.0 291.5 [25] 292.0 292.5 293.0 293.5 294.0 294.5 295.0 295.5 296.0 296.5 297.0 297.5 [37] 298.0 298.5 299.0 299.5 300.0 300.5 301.0 301.5 302.0 302.5 303.0 303.5 [49] 304.0 304.5 305.0 305.5 306.0 306.5 307.0 307.5 308.0 308.5 309.0 309.5 [61] 310.0 310.5 311.0 311.5 312.0 312.5 313.0 313.5 314.0 314.5 315.0 315.5 [73] 316.0 316.5 317.0 317.5 318.0 318.5 319.0 319.5 320.0 320.5 321.0 321.5 [85] 322.0 322.5 323.0 323.5 324.0 324.5 325.0 325.5 326.0 326.5 327.0 327.5 [97] 328.0 328.5 329.0 329.5 330.0 330.5 331.0 331.5 332.0 332.5 333.0 333.5 [109] 334.0 334.5 335.0 335.5 336.0 336.5 337.0 337.5 338.0 338.5 339.0 339.5 [121] 340.0 340.5 341.0 341.5 342.0 342.5 343.0 343.5 344.0 344.5 345.0 345.5 [133] 346.0 346.5 347.0 347.5 348.0 348.5 349.0 349.5 350.0 350.5 351.0 351.5 [145] 352.0 352.5 353.0 353.5 354.0 354.5 355.0 355.5 356.0 356.5 357.0 357.5 [157] 358.0 358.5 359.0 359.5 360.0 360.5 361.0 361.5 362.0 362.5 363.0 363.5 [169] 364.0 364.5 365.0 365.5 366.0 366.5 367.0 367.5 368.0 368.5 369.0 369.5 [181] 370.0 370.5 371.0 371.5 372.0 372.5 373.0 373.5 374.0 374.5 375.0 375.5 [193] 376.0 376.5 377.0 377.5 378.0 378.5 379.0 379.5 380.0 |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
> #combination of t prior with normal likelihood > > > chol <- c(274.8501,208.6479,286.7656,413.5640,344.2833,292.2896,296.8147, + 198.4725, 466.3404, 422.0513, 158.3340, 252.9971, 316.3647, 237.2512, + 381.1431, 131.5190, 300.1888, 341.7261, 487.6174, 200.7114, 216.6859, + 466.1822, 455.6942, 449.0033, 290.7924, 275.1898, 292.9542, 328.8997, + 99.7303, 275.1126, 366.7504, 272.8722, 436.3839, 160.2993, 269.5784, + 394.8876, 234.3379, 449.0895, 153.6546, 301.6407, 376.8302, 381.5326, + 378.2189, 607.6112, 162.4040, 251.7461, 274.9384, 272.1369, 712.3612, + 283.9782) > > length(chol) [1] 50 |
IBBENS-2調査では50名、標本平均318.07、標本分散285.57
|
1 2 3 4 5 6 7 8 |
> > samplemu <- mean(chol) > samplevar <- var(chol)/length(chol) > > samplemu [1] 318.0686 > samplevar [1] 285.5715 |
事前分布をt分布を選択するなら、
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 |
> # Prior = t-distribution > > # df = degrees of freedom of t-distribution > > df.tdist <- 30 > > > poster <- function(x) + { + #xbar <- 318.07 + #var <- 14278.6/50 + xbar <- mean(chol) #コレステロール標本平均をxbar + var <- var(chol)/length(chol) #コレステロール標本分散をvar + pmu <- priormu #事前分布(IBBENS調査1)の平均 + pvar <- priorvar #事前分布(IBBENS調査1)の分散 + df <- df.tdist #t=30 + vdf <- df/(df-2) #自由度 + + part1 <- dnorm(x,xbar,sqrt(var)) #標本正規分布 + part2 <- dt((x-pmu)/sqrt(pvar/vdf),df)/sqrt(pvar/vdf) #事前t分布 + + poster <- part1*part2 #尤度*事前分布=事後分布 + poster + } > > constant <- integrate(poster,lower=mumin,upper=mumax)$value #積分 > > print(constant) [1] 0.01789462 > > relpost <- poster(mu)/constant #積分値で事後分布の正規化 |
|
1 2 3 4 5 6 |
> relpost [1] 3.881143e-07 4.797221e-07 5.923358e-07 7.306119e-07 9.001981e-07 [6] 1.107934e-06 1.362091e-06 1.672653e-06 2.051657e-06 2.513587e-06 ..... [196] 6.530931e-09 5.082851e-09 3.952060e-09 3.069941e-09 2.382503e-09 [201] 1.847310e-09 |
事前分布に正規分布を選択するなら、解析的に公式を使って事後分布を求める。
|
1 2 3 4 5 6 7 8 9 10 11 12 |
> #Prior = normal distribution > > > weight0 <- 1/priorvar #事前精度 > weight1 <- 1/samplevar #サンプル標本精度 > postvar <- 1/(weight0+weight1) #事後分散 > weight0 <- weight0*postvar > weight1 <- weight1*postvar > postmu <- weight0*priormu+weight1*samplemu #事後平均 > > > vdf <- df.tdist/(df.tdist-2) |
|
1 2 3 4 5 6 |
> #PLOT posterior distributions > > > par(mfrow=c(1,1)) > par(pty="m") > par(mar=c(5,5,4,2)+0.1) |
まずはグラフの枠を作成し、
|
1 |
> plot(mu,relpost,xlab="MU",ylab="Density",type="n",ylim=c(0,0.05)) |
|
1 2 3 4 |
> lines(mu,dt((mu-pmu)/sqrt(priorvar/vdf),df)/sqrt(priorvar/vdf),lty=4, + lwd=2,col="red") > text(365,0.01,"t-prior",adj=0,col="red",cex=1.3) > arrows(365,0.008,360,0.001,col="red",length=0.2) |
|
1 2 3 4 |
> lines(mu,relpost,lwd=5,col="dark red") > text(290,0.015,"t-posterior",adj=0,col="dark red",cex=1.3) > arrows(298,0.013,309,0.011,col="dark red",length=0.2) > |
|
1 2 3 |
> lines(mu,dnorm(mu,priormu,sqrt(priorvar)),lty=1,lwd=2,col="blue") > text(350,0.03,"Normal-prior",adj=0,col="blue",cex=1.3) > arrows(350,0.028,340,0.023,col="blue",length=0.2) |

その場合の事後分布は、N(325.4242, 8.606072)
|
1 2 3 |
> lines(mu,dnorm(mu,postmu,sqrt(postvar)),lty=6,lwd=4,col="dark blue") > text(290,0.04,"Normal-posterior",adj=0,col="dark blue",cex=1.3) > arrows(307,0.04,322,0.045,col="dark blue",length=0.2) |
事前分布に正規分布N(328, 100)を選んでも、T分布t30(328, 100)を選んでも、事後分布は実質的には変わらない。しかし、t分布を選んだ場合は、
1)事後分布は解析的には求められない
2)事後分布が事前分布と同じ分布族には属さない
3)事後要約量が事前分布や標本要約量の簡単な関数ではない。
5.3.2 正規分布ー平均と分散が未知
5.3.3 多変量分布
5.3.4 条件付き共役と準共役事前分布
5.3.5 超事前分布
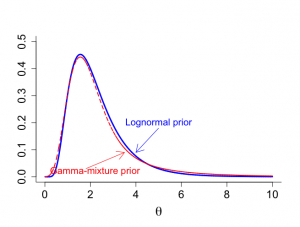
例V.3 虫歯研究:対数正規事前分布の近似
dmft指数の平均を表すθに対して、対数正規事前分布を仮定した。この事前分布の欠点は、事後分布の要約量がサンプリングによってのみ可能であることである。そこで、うまく選択された3つのガンマ分布の混合で対数政治事前分布を近似する。
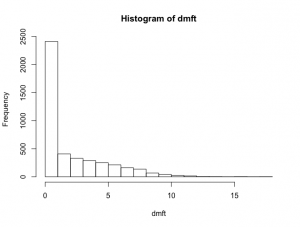
dmftのデータがどんなデータだったか、もう一度分析するところから始める。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
> dmft =read.delim("dmft.txt", header=TRUE) > objects(2) [1] "Y" > dmft <- Y > table(dmft)/4351 dmft 0 1 2 3 4 5 0.4396690416 0.1144564468 0.0937715468 0.0756148012 0.0666513445 0.0574580556 6 7 8 9 10 11 0.0489542634 0.0367731556 0.0314870145 0.0153987589 0.0091932889 0.0052861411 12 13 14 16 18 0.0034474833 0.0006894967 0.0004596644 0.0004596644 0.0002298322 > mdmft <- mean(dmft) > length(dmft) [1] 4351 > hist(dmft) |
混合分布と対数正規事前分布の間の距離を最小にするグリッド検索によって、次の混合分布の構成が与えられた。
(1) π1=0.15, α1=2.5, β1=1.75
(2) π2=0.3, α2=3.8, β2=0.67
(3) π3=0.55, α3=6, β3=0.3
これが、どうやって選ばれたのか、チンプンカンプン!
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 |
> # advanced sampling from combination log-normal & Poisson > > gridsize <- 0.001 > gtheta <- seq(0.01,10,gridsize) > ntheta <- length(gtheta) > > # prior = log-normal > > sigma0 <- 0.5 > mu0 <- log(2) > pi <- 3.14159 > > fact1 <- 1/(gtheta*sigma0*sqrt(2*pi)) > fact2 <- exp(-0.5*(log(gtheta)-mu0)^2/sigma0^2) > priortheta <- fact1*fact2 > > sum(priortheta)*gridsize [1] 0.9993572 > > # after a grid search these are the 'best gamma parameters' > > pip.f <-c(0.15, 0.30, 0.55) > shape.f <- c(2.5, 3.8, 6) > scale.f <- c(1.75,0.667,0.3) > > gtheta.begin <- gtheta[1:ntheta/1] > mixturemin <- pip.f[1]*dgamma(gtheta.begin,shape.f[1],scale=scale.f[1])+ + pip.f[2]*dgamma(gtheta.begin,shape.f[2],scale=scale.f[2])+ + pip.f[3]*dgamma(gtheta.begin,shape.f[3],scale=scale.f[3]) > > fact1.begin <- 1/(gtheta.begin*sigma0*sqrt(2*pi)) > fact2.begin <- exp(-0.5*(log(gtheta.begin)-mu0)^2/sigma0^2) > priortheta.begin <- fact1.begin*fact2.begin > > > maxy <- max(c(dgamma(gtheta.begin,shape.f[1],scale=scale.f[1]), + dgamma(gtheta.begin,shape.f[2],scale=scale.f[2]), + dgamma(gtheta.begin,shape.f[3],scale=scale.f[3]))) > > par(mar=c(5,4,4,2)+0.1) > > par(mfrow=c(1,1)) > par(pty="m") > > plot(gtheta.begin,priortheta.begin,xlab=expression(paste(theta)), + ylab="",type="n",bty="l",ylim=c(0,0.5),cex.lab=1.8,cex=1.2,cex.axis=1.5) > lines(gtheta.begin,priortheta.begin,lwd=3,col="blue") > lines(gtheta.begin,mixturemin,lty="dashed",lwd=2,col="red") > text(5,0.2,"Lognormal prior",col="blue",cex=1.3) > arrows(5,0.18,4,0.09,,col="blue",length=0.2) > text(2.2,0.02,"Gamma-mixture prior",col="red",cex=1.3) > arrows(1.8,0.03,3.5,0.09,col="red",length=0.2) > > # posterior mean & posterior variance > > sumy <- 26 > ny <- 10 > > alphaprior1 <- shape.f[1] > betaprior1 <- scale.f[1] > alphaprior2 <- shape.f[2] > betaprior2 <- scale.f[2] > alphaprior3 <- shape.f[3] > betaprior3 <- scale.f[3] > > alphapost1 <- alphaprior1+sumy > betapost1 <- betaprior1+ny > alphapost2 <- alphaprior2+sumy > betapost2 <- betaprior2+ny > alphapost3 <- alphaprior3+sumy > betapost3 <- betaprior3+ny > > #posterior weights > > pop.f <- rep(NA,3) > temp1 <- exp(alphaprior1*log(betaprior1) - alphapost1*log(betapost1) -lgamma(alphaprior1) + lgamma(alphapost1)) > temp2 <- exp(alphaprior2*log(betaprior2) - alphapost2*log(betapost2) -lgamma(alphaprior2) + lgamma(alphapost2)) > temp3 <- exp(alphaprior3*log(betaprior3) - alphapost3*log(betapost3) -lgamma(alphaprior3) + lgamma(alphapost3)) > denom <- pip.f[1]*temp1+pip.f[2]*temp2+pip.f[3]*temp3 > pop.f[1] <- temp1*pip.f[1]/denom > pop.f[2] <- temp2*pip.f[2]/denom > pop.f[3] <- temp3*pip.f[3]/denom > > #posterior mean and variance of mixture > > meangamma <- c(alphapost1 /betapost1,alphapost2/betapost2, + alphapost3/betapost3) > meanpost <- pop.f%*%meangamma > > vargamma.a <- c(alphapost1/betapost1^2,alphapost2/betapost2^2, + alphapost3/betapost3^2) > varpost.a <- pop.f%*%vargamma.a > vargamma.b <- c((alphapost1/betapost1-meanpost)^2, + (alphapost2/betapost2-meanpost)^2, + (alphapost3/betapost3-meanpost)^2) > varpost.b <- pop.f%*%vargamma.b > varpost <- varpost.a+varpost.b |
5.4 無情報事前分布
5.4.1 はじめに
Noninformative (NI) prior distribution 無情報事前分布:
情報の欠如や無知を表す無情報事前分布は、実際には無情報ではなく、何かしらの情報を含んでいると考えるべきである(弱や拡散というほうがふさわしいかも)。厳密には、非正則分布improperと呼ばれる。非正則improperとは積分しても収束しない。
5.4.2 無情報
事前情報をもたないとき、「無関心の原則principle of indifferece」と呼ばれる
「不十分な理由の原則principle of insufficient reason」= ベイズ・ラプラスの公準Bayes-Laplace postulateとも呼ばれる。
厳密には、情報がないことを表現できる事前分布はない。
5.4.3 無情報事前分布選択の一般原理
Jeffreys事前分布
Jeffreys不変原則Jeffreys invariance principle of rule
事前分布をフィッシャーの情報行列の平方根に比例するように定める。
「一つのパラメータθに対する事前分布は事前分布がフィッシャーの情報量の平方根に比例するとき、近似的に無情報である」
ψ ∝ ∫ F^(1/2)(θ)dθ
フィッシャーの情報行列とは?
フィッシャー情報量は、確率変数がパラメーターに関して持つ情報量のことである。
スコア関数の分散はフィッシャー情報量として定義されている。スコア関数の分散は次のように式変換することで、尤度関数の偏微分として表すことができる。スコア関数の θ が複数ある場合、フィッシャー情報量は行列として表すことができる。
パラメータ θ
を持つ確率密度関数:f(x,θ)
で表される分布について考えます。
1.尤度関数:
L(θ;x1)=f(x1,θ)
(尤度関数と確率密度関数は意味が異なります,詳細は統計の本を参照して下さい)。
2.対数尤度関数:
logL(θ;x1)=logf(x1,θ)
尤度関数は対数を取った方が計算しやすい場合が多いのでけっこう登場します。
スコア関数とフィッシャー情報量
3.スコア関数:
∂∂θlogL=1L∂L∂θ
対数尤度関数をパラメータで偏微分したものです。スコア関数は観測値 x1
の関数なので,確率変数です。従って,期待値や分散を考えることができます。
そして,スコア関数の期待値は 0
です(証明は後述)。そのため,スコア関数の分散は二次モーメントと一致します。この量をフィッシャー情報量と言います。
4.フィッシャー情報量(パラメータの関数):
Var[∂∂θlogL]=E[(∂∂θlogL)2]
Jeffreys事前分布
ポアソン分布: p(θ) ∝ θ^(-1/2) フラット事前分布に対応
σが既知の正規分布: p(μ)∝c
μが既知の正規分布: p(σ-2)∝σ^(-2)
p(θ) ∝ |F(θ)|^(1/2)
データ変換尤度原理data-translated likelihood principle, DLT
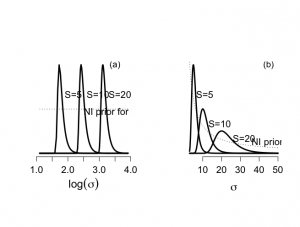
μが与えられたもとで、σに対する正規分布の尤度は、
L(σ|μ, y) ∝ σ^(-n)*exp(-nS^2/2σ^2), S^2 = Σ(yi -μ)^2
n=10で、標準偏差Sが、5, 10, 20の3つのデータを仮定すると、σの関数としての尤度は、位置と形状が変化するが、log(σ)の関数では、位置のみが変化する。
log(σ)に対するフラット事前分布は、p(σ)∝σ^(-1)、p(σ^2)∝σ^(-2):=Jeffreys事前分布
例V.4 μが与えられたもとでの正規分布のσの尤度へのDTL原理の適応
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 |
> par(mfrow=c(1,2)) > par(pty="s") > > sigmin <- 1 > sigmax <- 50 > s <- c(5,10,20) > size <- 10 > factor <- 1 > > gridsize <- (sigmax-sigmin)/200 > sigma <- seq(sigmin,sigmax,gridsize) > lsigma <- length(sigma) > > > #EXAMPLE LIKELIHOODS FOR SIGMA ON TRANSFORMED SCALE > > sigmin <- 3 > sigmax <- 50 > s <- c(5,10,20) > size <- 10 > factor <- 1 > > gridsize <- (sigmax-sigmin)/200 > sigma <- seq(sigmin,sigmax,gridsize) > lsigma <- length(sigma) > > > term1 <- log(sigma)-log(s[1]) > term2 <- log(sigma)-log(s[2]) > term3 <- log(sigma)-log(s[3]) > > lik1 <- exp(-size*term1 - 0.5*size*exp(-2*size*term1)) > lik2 <- exp(-size*term2 - 0.5*size*exp(-2*size*term2)) > lik3 <- exp(-size*term3 - 0.5*size*exp(-2*size*term3)) > > lik1 <- lik1/max(lik3) > lik2 <- lik2/max(lik3) > lik3 <- lik3/max(lik3) > > > plot(log(sigma),lik1,xlab=expression(paste(log(sigma))),ylab="",type="n",bty="n", + yaxt="n",main="",cex.lab=1.5,cex.axis=1.3) > lines(log(sigma),lik1,lty=1,lwd=3) > text(1.9,2*max(lik1)/3,"S=5",adj=0,cex=1.3) > text(3.5,max(lik1),"(a)",cex=1.2) > > lines(log(sigma),lik2,lty=1,lwd=3) > text(2.6,2*max(lik1)/3,"S=10",adj=0,cex=1.3) > > lines(log(sigma),lik3,lty=1,lwd=3) > text(3.3,2*max(lik1)/3,"S=20",adj=0,cex=1.3) > > lines(log(sigma),rep(factor,length(sigma))*.5,lty=3) > text(2.5,0.95*max(lik1)/2,expression(paste("NI prior for ",log(sigma))),adj=0,cex=1.3) > > #CORRESPONDING LIKELIHOODS FOR SIGMA ON ORIGINAL SCALE > > term1 <- exp(-0.5*size*s[1]^2/sigma^2) > term2 <- exp(-0.5*size*s[2]^2/sigma^2) > term3 <- exp(-0.5*size*s[3]^2/sigma^2) > > lik1 <- (sigma^(-size))*term1 > lik2 <- (sigma^(-size))*term2 > lik3 <- (sigma^(-size))*term3 > > lik1 <- lik1*10^6/(sum(lik1)*gridsize) > lik2 <- lik2*10^6/(sum(lik2)*gridsize) > lik3 <- lik3*10^6/(sum(lik3)*gridsize) > > > plot(sigma,lik1,xlab=expression(paste(sigma)),ylab="",type="n", + bty="n",yaxt="n",main="",cex.lab=1.5,cex.axis=1.3) > lines(sigma,lik1,lty=1,lwd=3) > text(6.5,2*max(lik1)/3,"S=5",adj=0,cex=1.3) > text(45,max(lik1),"(b)",cex=1.2) > > lines(sigma,lik2,lty=1,lwd=3) > text(13,2*max(lik2)/3,"S=10",adj=0,cex=1.3) > > lines(sigma,lik3,lty=1,lwd=3) > text(26,2*max(lik3)/3,"S=20",adj=0,cex=1.3) > > lines(sigma,10^6*rep(factor,length(sigma))/sigma,lty=3) > text(36,max(lik3)/2,expression(paste("NI prior for ",sigma)),adj=0,cex=1.3) |
5.4.4 非正則事前分布
多くの無情報(NI)事前分布は正則な分布でない。
5.4.5 弱情報/漠然事前分布
弱情報事前分布: σ0の大きい正規分布N(0, σ0^2)とか、逆ガンマ事前分布IG(ε,ε):
ε->∞ で、Jeffreys事前分布p(σ^2)∝σ-2となる。
5.5 情報のある事前分布
5.5.1 はじめに
a) 過去のデータをべき事前分布power priorを用いて事前情報として形式化する。
b) 過去のデータまたは専門家の知識にものづく事前分布である臨床事前分布clinical prior
c) 事前の懐柔主義や楽観主義を表す形式的ルールに基づく事前分布を用いる。
5.5.2 データにもとづく事前分布
過去のデータは現在のデータと同じ条件下で実現されたと仮定し、過去のデータからの事前情報と現在のデータの尤度を結合することである。
<Ibrahim and Chenの提案>
p(θ|y, y0, α0) ∝ L(θ|y)L(θ|y0)^α0*p0(θ|c0)
α0=0のとき、過去のデータは無視、α0=1であるとき、過去のデータは現在のデータと同じ重みが与えられる。ただし、どのようなα0を選ぶのかは、すぐにはわからない。
5.5.3 事前知識の抽出(専門家の知識による事前分布)
例V.5: 脳卒中試験:専門家知識による第1回目の中間解析に対する事前分布
rt-PA治療患者に対するSICHの発生率θに関して、過去のデータはないとする。
こそで専門家の知識の抽出:
(1)θに対する最も当てはまりそうな値(事前分布の最頻値、平均値、あるいは中央値として解釈)
(2)θにたいする不確実性は、例えば95%等裾確率CIとして表現。
ー>例えば、θに対する事前分布の最頻値を0.10で、事前95%等裾確率CIを[0.05, 0.20]と仮定する。ー>Beta(7.2, 56.2)
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 |
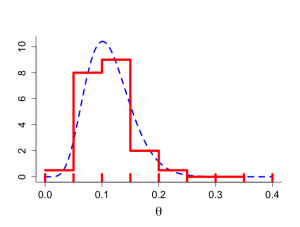
> # figure 5.3 > > par(mar=c(5,4,4,2)+0.1) > > par(mfrow=c(1,1)) > par(pty="m") > > alpha <- 7.2 > beta <- 56.2 > mode <- (alpha-1)/(alpha+beta-2) > mean <- alpha/(alpha+beta) > q025 <- qbeta(0.025,alpha,beta) > q975 <- qbeta(0.975,alpha,beta) > begin <- 0 > end <- 0.4 > > mode;mean;q025;q975 [1] 0.1009772 [1] 0.1135647 [1] 0.04841262 [1] 0.2016561 > > theta <- seq(begin,end,0.001) > grid <- seq(begin,end,0.05) > ngrid <- length(grid) > midpoint <- (grid[1:(ngrid-1)]+grid[2:ngrid])/2 > dbetamid <- dbeta(midpoint,alpha,beta) > prob <- dbetamid*0.05 > sum(prob*100) [1] 100.1964 > dbetamid <- c(0.025,0.40,0.45,0.10,0.025,0,0,0)/0.05 > dtheta <- dbeta(theta,alpha,beta) > > > plot(theta,dtheta,type="n",xlab=expression(paste(theta)), + ylab=" ",bty="l",cex.lab=1.8,cex=1.2,cex.axis=1.4) > lines(theta,dtheta,lwd=3,lty="dashed",col="blue") > lines(grid[1:(ngrid-1)],dbetamid,type="s",lwd=5,col="red") > for (igrid in 1:ngrid){ + segments(grid[igrid],-0.5,grid[igrid],0.2,lwd=5,col="red") + } |
5.5.3.2識別可能性の問題
ある状況では、強力な主観的事前情報が事後の推定値にたどり着くために不可欠なときがある。
データがモデルの全パラメータを推定するのに十分でない時、モデルは識別不能nonidentifiableと呼ばれる。尤度識別可能とは、すなわち尤度がモデルパラメータのゆいちの推定値を提供するのに十分であるという意味。「強力な事前情報ー>全パラメータについて合理的な事後情報を得る」
ということもある。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 |
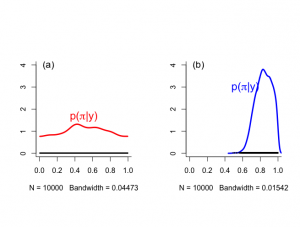
> # the results are in file cys1 > > library(coda) > > # set working directory to where the coda files are located > > a1 <- read.coda("cys1.txt","cysindex.txt") Abstracting pi ... 10000 valid values Abstracting sens ... 10000 valid values Abstracting spec ... 10000 valid values > a2 <- read.coda("cys2.txt","cysindex.txt") Abstracting pi ... 10000 valid values Abstracting sens ... 10000 valid values Abstracting spec ... 10000 valid values > > > #--------------------------------------------------------------------- > # more flexible plots > #--------------------------------------------------------------------- > > par(mfrow=c(1,2)) > par(bty="l") > par(pty="s") > > # density plot > #---------------------------------------------------------------------- > #---------------------------------------------------------------------- > # > > densplot(a1[,"pi"],show.obs=TRUE,ylim=c(0,4),lwd=3,main="",xlim=c(0,1), + col="red") > text(0.1,4,"(a)",cex=1.3) > text(0.5,1.67,expression(paste("p(",pi,"|y)")),cex=1.5,col="red") > densplot(a2[,"pi"],show.obs=TRUE,ylim=c(0,4),lwd=3,main="",xlim=c(0,1), + col="blue") > text(0.1,4,"(b)",cex=1.3) > text(0.63,3,expression(paste("p(",pi,"|y)")),cex=1.5,col="blue") |
5.5.4 典型的な事前分布
懐疑的skeptical事前分布と熱狂的enthusiastic事前分布
5.5.4.1 懐疑的事前分布
例V.7:第?相ランダム化試験における懐疑的事前分布の利用
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 |
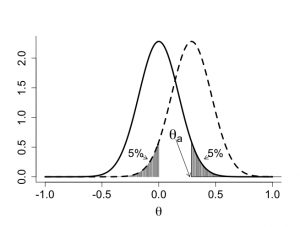
> # archetypal skeptical prior > > par(mar=c(5,4,4,2)+0.1) > > par(mfrow=c(1,1)) > par(pty="m") > > z <- seq(-1,1,0.01) > > thetaA <- log(25/18.75) > gamma <- 0.05 > > zgamma <- qnorm(gamma,0,1) > > sigma0 <- -thetaA/zgamma > > dzscept <- dnorm(z,0,sigma0) > dzenthu <- dnorm(z,thetaA,sigma0) > > par(mfrow=c(1,1)) > par(pty="m") > > plot(z,dzscept,type="n",xlab=expression(paste(theta)),ylab="", + bty="l",cex.lab=1.8,cex=1.2,cex.axis=1.5) > lines(z,dzscept,lwd=3,lty=1) > lines(z,dzenthu,lwd=3,lty=2) > #legend(-1,2.4,c("skeptical prior","enthusiastic prior"), > #lty=c(1,4)) > #segments(0,0,0,dnorm(0,thetaA,sigma0)) > #segments(0,0,-10,0) > > segments(thetaA,0,thetaA,dnorm(thetaA,0,sigma0)) > segments(thetaA,0,10,0) > > nskep <- 206 > nenth <- 101 > > for (i in 1: nenth){ + segments(z[i],0,z[i],dzenthu[i]) + } > > for (i in 130:nskep){ + segments(z[i],0,z[i],dzscept[i]) + } > > text(0.15,0.7,expression(paste(theta[a])),cex=2) > arrows(0.15,0.63,0.273,0,length=0.1) > > text(0.5,0.4,"5%",cex=1.5) > arrows(0.45,0.35,0.4,0.3,length=0.1) > > text(-0.2,0.4,"5%",cex=1.5) > arrows(-0.15,0.35,-0.1,0.3,length=0.1) |
5.5.4.2 熱狂的事前分布
例V.9:脂質軽減ランダム化臨床試験:熱狂的事前分布の利用
5.6 回帰モデルにおける事前分布
5.7 事前分布のモデル化
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 |
> # solution to partial separation problem > > a <- -13.15 > b <- 1.492 > c <- 1.262 > > a1 <- 0;b1 <- -a/c > a2 <- 10; b2 <- -(a+10*b)/c > > segments(a1,b1,a2,b2,lwd=3,lty=3) > > # using Gelman's approach > > mean(x1);sqrt(var(x1/5.9)) [1] 4.428571 [1] 0.5006538 > mean(x2);sqrt(var(x2/5.62)) [1] 5.285714 [1] 0.5005059 > > a <- 0.002308 - 1.788*mean(x1)/5.9 - 1.058*mean(x2)/5.62 > b <- 1.492/5.9 > c <- 1.262/5.62 > > a1 <- 0;b1 <- -a/c > a2 <- 10; b2 <- -(a+10*b)/c > > segments(a1,b1,a2,b2,lwd=3,lty=5) |
5.8 その他の回帰モデル