Bayesian Biostatistics by E Lesaffre & AB Lawson, Chapter 3 学習ノート ???????????????????????
3.7 事後分布に対する数値計算
3.7.1 数値積分
3.7.2 事後分布からのサンプリング
1) モンテカルロ積分
2) 汎用サンプリングアルゴリズム
Bayesian Biostatistics の第3章のサンプリング理論に関する解説は、いきなり難しい解説と数式の嵐でとても理解しづらい。「そもそもサンプリング法とは何をしているのか!」ということを理解しないと、暗号解読のような作業に陥る。
むしろ、Rでのプログラミングで、サンプリングの例をあげて理解を進めるほうが、遥かに簡単である。
まずは、棄却アルゴリズムの具体例を知ることで、サンプリングとはという感覚を身につける。
|
1 2 3 4 5 6 7 |
> par(family = "HiraKakuProN-W3") > k <- 2.3 > plot(function(x){dgamma(x,shape=10)},0,30, + ylab="",col="red",lwd=3) > plot(function(x){k*dcauchy(x,scale=5,location=10)},0,30,add=TRUE,col="blue",lwd=3) > title(main="棄却サンプリング") > legend(15,0.12,c("ガンマ関数","一般化されたコーシー分布"),lwd=3,col=c("red","blue")) |
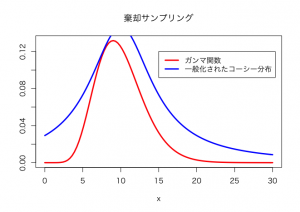
ここでは、ガンマ関数はサンプリングできない目標関数target distributionと仮にしておく。サンプリング可能な一般化されたコーシー分布を包絡関数envelope functionとして係数k=2.3として覆いかぶせる。このときに以下のプログラムで、コーシー分布からrcauchy()で乱数Xを発生させ、ガンマ分布との比率をdgamma(x,shape=10) / (2.3 * dcauchy(x,scale=5,location=10)を alpha として算定。0〜1の一様分布に基づく乱数uを発生させて、uとalphaの比較において、u<alphaであれば、xを採択し、そうでなければxを棄却する。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
accept = 0 reject = 0 myrand <- function(){ x <- rcauchy(1,scale=5,location=10) alpha <- dgamma(x,shape=10) / (k * dcauchy(x,scale=5,location=10)) u <- runif(1) if(u < alpha){ accept <<- accept + 1 print("accept") print(accept) res <- x return(res) }else{ print("false") reject <<- reject + 1 print("reject") print(reject) myrand() } } |
10000回繰り返して、発生したXをヒストグラムで頻度分布させる。つまり、棄却した場合、アクセプトされるまでルーチンを回して、結果としてアクセプトが10000回となる。
|
1 2 |
n <- 10000 hist(sapply(1:n,function(x){myrand()}), breaks = 100) |
|
1 2 3 4 |
[1] "reject" [1] 12997 [1] "accept" [1] 10000 |
12997回棄却して、10000回アクセプトされた。
|
1 2 |
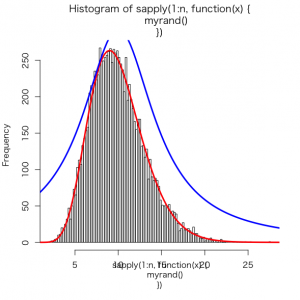
> plot(function(x){2000*dgamma(x,shape=10)},0,30, ylab="",add=TRUE, col="red",lwd=3) > plot(function(x){2.3*2000*dcauchy(x,scale=5,location=10)},0,30,add=TRUE,col="blue",lwd=3) |
棄却サンプリング
参考>http://aidiary.hatenablog.com/entry/20140712/1405165815
受理・棄却法では目標分布fと提案分布g*1という二つの分布を使う。目標分布fにしたがう乱数を生成するのが最終目的だが、目標分布fの乱数は直接生成できないため代わりに提案分布gの乱数を生成し、ある条件を満たす場合だけ生成した乱数を目標分布fの乱数とみなすというアプローチが受理・棄却法。条件を満たさない乱数は単に捨てられる。このとき、目標分布fと提案分布gの関係にはいくつか仮定がある。
1) 目標分布fにしたがう乱数は直接生成できない
2) 逆に提案分布gにしたがう乱数は生成できる
3) 目標分布fと提案分布gの確率密度関数は既知
4) すべての x について f(x) <= M * g(x) となる M が存在する
アルゴリズム:受理・棄却法
以下の手順で生成した乱数 X は目標分布fにしたがう乱数となる。
1. 提案分布gにしたがう乱数 Y を生成する
2. [0,1] の一様乱数Uを生成する
3. U*M*g(Y) <= f(Y)であれば Y を X として受理
4. そうでなければ Y を棄却し、1に戻る。
ーーーーーーー
重点サンプリング
|
1 2 |
> plot(function(x){dgamma(x,shape=10)},0,30) > plot(function(x){dcauchy(x,scale=2.5,location=10)},0,30,add=TRUE) |
|
1 2 3 4 5 6 7 |
> hist(w) > hist(w, breaks = 100) > t <- 10000 > x <- rcauchy(t,scale=2.5,location=10) > w <- dgamma(x,shape=10) / (dcauchy(x,scale=2.5,location=10)) > sum(w*x) / t [1] 10.02564 |
prob=w/sum(w)で5000回サンプリングをsample()関数で繰り返すと、目標関数とみごとに一致した。
|
1 2 3 4 5 |
> m <- 5000 > plot(function(x){dgamma(x,shape=10)},0,30) > plot(function(x){dcauchy(x,scale=2.5,location=10)},0,30,add=TRUE) > lines(density(sample(x, m, replace=TRUE, prob=w/sum(w))), col="red") > legend(23, 0.09, c("cauchy", "Estimated"), lwd=1, col=c("black", "red")) |
<重点サンプリング>
モンテカルロ法における分散減少法のひとつ. サンプリングすべき領域から, 自然に考えられる本来の確率分布にしたがってサンプルをとるのではなく, 重要と考えられる領域により大きな重みを置いてサンプルをとる方法である. 例えばきわめて稀にしか起きない現象の生起確率を推定したい場合に, この現象が実際よりずっと頻繁に起きるような確率分布にしたがってサンプルをとり, 推測の段階で本来の生起確率に換算するという使い方をする.