Bayesian Biostatistics by E Lesaffre & AB Lawson, Chapter 3 学習ノート
???????????????????????
この章は、ベイズの特徴を理解する上で重要そうであるが、内容はたいへん厳しい。
交換可能性、モンテカルロ法、ベイズファクター等、重要事項について読み進める。
???????????????????????
3.1 はじめに
3.2 確率による事後分布の要約
脳卒中試験、SICHの発症率
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
> # probabilities based on posterior > > alfa <- 19 > beta <- 133 > > # probability greater than 0.2 > > x <- 0.2 > > 1-pbeta(x,alfa,beta) [1] 0.006213874 > > # probability lower than 0.088 (value obtained from ECASS 2 study) > > y <- 0.088 > > pbeta(y,alfa,beta) [1] 0.07241627 > > # probability between 0.088 and 0.2 > > pbeta(x,alfa,beta)-pbeta(y,alfa,beta) [1] 0.9213699 |
3.3 事後分布の要約量
脳卒中試験、事後分布の要約量
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
> # computation posterior measures stroke study > > alpha <- 19 > beta <- 133 > > pmode <- (alpha-1)/(alpha+beta-2);pmode [1] 0.12 > > pmean <- alpha/(alpha+beta);pmean [1] 0.125 > > pmedian <- qbeta(0.5,alpha,beta);pmedian [1] 0.1233544 > > pvar <- alpha*beta/((alpha+beta)^2*(alpha+beta+1));pvar [1] 0.0007148693 > psd <- sqrt(pvar);psd [1] 0.02673704 |
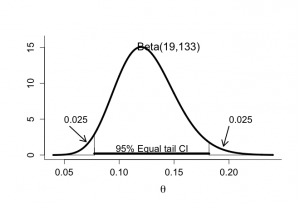
脳卒中試験:SIVCHの発症率の区間推定
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 |
> # equal 95% tail CI > > par(mfrow=c(1,1)) > par(pty="m") > > > theta <- seq(0.04,0.24,0.0001) > plot(theta, dbeta(theta,alpha,beta),xlab=expression(theta), + ylab="", type="n",ylim=c(0,16),bty="l",cex.lab=1.5,cex=1.2,cex.axis=1.3) > lines(theta,dbeta(theta,alpha,beta),lwd=4,lty=1) > text(0.145,15,"Beta(19,133)",cex=1.5) > > segments(qbeta(0.025,alpha,beta),0,qbeta(0.025,alpha,beta),1) > segments(qbeta(0.975,alpha,beta),0,qbeta(0.975,alpha,beta),1) > > segments(qbeta(0.025,alpha,beta),0.2,qbeta(0.975,alpha,beta), + 0.2,lwd=5) > text(0.13,0.8,"95% Equal tail CI",cex=1.3) > > segments(qbeta(0.025,alpha,beta),0,qbeta(0.025,alpha,beta), + dbeta(qbeta(0.025,alpha,beta),alpha,beta)) > segments(0.04,0,qbeta(0.025,alpha,beta),0) > > segments(qbeta(0.975,alpha,beta),0,qbeta(0.975,alpha,beta), + dbeta(qbeta(0.975,alpha,beta),alpha,beta)) > segments(qbeta(0.975,alpha,beta),0,0.24,0) > > text(0.05,5,"0.025",adj=0,cex=1.3) > arrows(0.055,4,0.07,dbeta(0.07,alpha,beta)+0.5,length=0.15,lwd=2) > text(0.20,5,"0.025",adj=0,cex=1.3) > arrows(0.20,4,0.195,dbeta(0.195,alpha,beta)+0.5,length=0.15,lwd=2) |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 |
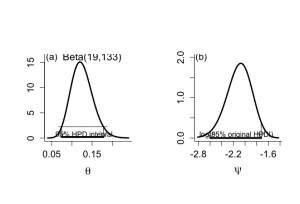
# figure 3.2 par(mar=c(5,5,4,2)+0.1) alpha <- 19 beta <- 133 # figure 3.2(a) 95% HPD interval par(mfrow=c(1,2)) par(pty="s") theta <- seq(0.04,0.24,0.0001) plot(theta, dbeta(theta,alpha,beta),xlab=expression(theta), ylab="",bty="l",main="", type="n",ylim=c(0,16),cex.lab=1.5,cex.axis=1.3) lines(theta,dbeta(theta,alpha,beta),lwd=3,lty=1) text(0.15,16,"Beta(19,133)",cex=1.4) text(0.05,16,"(a)",cex=1.3) p2 <- alpha q2 <- beta f <- function(x,p=p2,q=q2){b<-qbeta(pbeta(x,p,q)+0.95,p,q);(dbeta(x,p,q)-dbeta(b,p,q))^2} hpdmin <- optimize(f,lower=0,upper=qbeta(0.05,p2,q2),p=p2,q=q2)$minimum hpdmax <- qbeta(pbeta(hpdmin,p2,q2)+0.95,p2,q2) hpdmin;hpdmax segments(c(hpdmin*.90),c(dbeta(hpdmin,p2,q2)), c(hpdmax*1.05),c(dbeta(hpdmin,p2,q2)),lty=1) arrows(c(hpdmin),c(dbeta(hpdmin,p2,q2)), c(hpdmin),c(0.2),length=.15) arrows(c(hpdmax),c(dbeta(hpdmax,p2,q2)), c(hpdmax),c(0.2),length=.15) segments(c(hpdmin),c(0.2),c(hpdmax),c(0.2),lwd=4) text(0.13,0.8,"95% HPD interval",cex=1) # figure 3.2(b) non-invariance of HPD interval alpha <- 19 beta <- 133 theta <- seq(0.06,0.24,0.0001) psi <- log(theta) xmin <- min(psi) xmax <- max(psi) coef <- lgamma(alpha+beta)-lgamma(alpha)-lgamma(beta) dpsi <- exp(coef)*exp(psi)^alpha*(1-exp(psi))^(beta-1) plot(psi, xlab=expression(psi),ylab="",type="n", xlim=c(xmin,xmax),ylim=c(0,2.0),bty="l",main="",cex.lab=1.5,cex.axis=1.3) lines(psi,dpsi,lwd=3) text(-2.75,2,"(b)",cex=1.3) dpsibeta <- function(x,p=alpha,q=beta){dbeta(exp(x),p,q)*exp(x)} psihpdmin <- log(hpdmin) psihpdmax <- log(hpdmax) arrows(c(psihpdmin),c(dpsibeta(psihpdmin,p2,q2)), c(psihpdmin),c(0),length=.15) arrows(c(psihpdmax),c(dpsibeta(psihpdmax,p2,q2)), c(psihpdmax),c(0),length=.15) segments(c(psihpdmin),c(0),c(psihpdmax),c(0),lwd=4) text(-2.15,0.08,"log(95% original HPDI)",cex=1) |
3.4 予測分布
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 |
> ALP = read.delim("ALP.txt", header=TRUE) > > # 95% reference interval serum alkaline phosphatase > > attach(ALP) > > objects(2) [1] "alkfos" "artikel" > > alp <- alkfos[artikel==0] > talp <- 100*alp^(-1/2) > nalp <- length(alp) > > meantalp <- mean(talp) > sdtalp <- sqrt(var(talp)) > meantalp;sdtalp [1] 7.108724 [1] 1.365344 > > > mintalp <- min(talp) > maxtalp <- max(talp) > refunltalp <- meantalp -1.96*sdtalp > refupltalp <- meantalp +1.96*sdtalp > > refunltalp2 <- meantalp -1.96*sdtalp*sqrt(1+1/nalp) > refupltalp2 <- meantalp +1.96*sdtalp*sqrt(1+1/nalp) > refunltalp2;refupltalp2 [1] 4.427302 [1] 9.790145 > > > minalp <- 10 > maxalp <- max(alp) > refuplapl <- 100^2/refunltalp^2 > refunlapl <- 100^2/refupltalp^2 > refuplapl2 <- 100^2/refunltalp2^2 > refunlapl2 <- 100^2/refupltalp2^2 > > refunlapl;refuplapl [1] 104.4471 [1] 508.9478 > refunlapl2;refuplapl2 [1] 104.333 [1] 510.1779 > > > gridalp <- seq(minalp,maxalp,1) > dfalp <- 50*dnorm(100/sqrt(gridalp),meantalp,sdtalp)/(sqrt(gridalp)^3) > par(bty="l") > > > par(mfrow=c(1,1)) > par(pty="m") > par(mar=c(5,5,4,2)+0.1) > > hist(alp,xlab="alp",nclas=20,prob=T,xlim=c(0,1000),col=0,main="", + ylab="", cex.lab=1.8,cex=1.2,cex.axis=1.3) > lines(gridalp,dfalp,lwd=3,col="red") > segments(refunlapl,0,refuplapl,0,lwd=10,col="blue") > text(265,0.0003,"95% Reference range",cex=1.1,col="dark blue") |

3.5 交換可能性
標本(y1, y2, …..yn}における独立性の仮定は、P(y1, y2, …,yn|θ)=Πp(yi|θ)と書ける。
独立性とはθで条件付けて定義されて、独立であるならば、結合分布は周辺分布の積に分解される。
θの条件付きでないyの結合分布は、
p(y1, y2, …,yn) = ∫p(y1,y2,…,yn|θ)p(θ)dθ = ∫Πp(yi|θ)p(θ)dθ
要するに結合確率は、それぞれのp(yi|θ)p(θ)の積の積分で表されるので、個別のyiの順序が入れ替わっても影響しない。つまり、結合確率
p(y1, y2, ….,yn) = p(yπ(1), yπ(2),…yπ(n))
この場合、確率変数y1, y2, …..ynは、交換可能exchangeableという。
3.6 事後分布に対する正規近似
3.7 事後分布に対する数値計算
3.7.1 数値積分
3.7.2 事後分布からのサンプリング
1) モンテカルロ積分
2) 汎用サンプリングアルゴリズム
棄却サンプリング
参考>http://aidiary.hatenablog.com/entry/20140712/1405165815
受理・棄却法では目標分布fと提案分布g*1という二つの分布を使う。目標分布fにしたがう乱数を生成するのが最終目的だが、目標分布fの乱数は直接生成できないため代わりに提案分布gの乱数を生成し、ある条件を満たす場合だけ生成した乱数を目標分布fの乱数とみなすというアプローチが受理・棄却法。条件を満たさない乱数は単に捨てられる。このとき、目標分布fと提案分布gの関係にはいくつか仮定がある。
1) 目標分布fにしたがう乱数は直接生成できない
2) 逆に提案分布gにしたがう乱数は生成できる
3) 目標分布fと提案分布gの確率密度関数は既知
4) すべての x について f(x) <= M * g(x) となる M が存在する
アルゴリズム:受理・棄却法
以下の手順で生成した乱数 X は目標分布fにしたがう乱数となる。
1. 提案分布gにしたがう乱数 Y を生成する
2. [0,1] の一様乱数Uを生成する
3. U*M*g(Y) <= f(Y)であれば Y を X として受理
4. そうでなければ Y を棄却し、1に戻る
<重点サンプリング>
モンテカルロ法における分散減少法のひとつ. サンプリングすべき領域から, 自然に考えられる本来の確率分布にしたがってサンプルをとるのではなく, 重要と考えられる領域により大きな重みを置いてサンプルをとる方法である. 例えばきわめて稀にしか起きない現象の生起確率を推定したい場合に, この現象が実際よりずっと頻繁に起きるような確率分布にしたがってサンプルをとり, 推測の段階で本来の生起確率に換算するという使い方をする.
3.8 ベイズ流仮説検定
3.8.1 信用区間にもとづく推論
帰無仮説H0: θ=θ0とする。θの信用区間95%CIを用いて、θ0がこの区間に含まれないとき、帰無仮説は棄却されたとみなせる。これはベイズ流回帰モデルにおける回帰係数の評価などの時によく用いられる。
帰無仮説に対する事後のエビデンスは投稿確率contour probability PB(以下に定義)を通しても表すことができる。
P(p(θ|y) > p(θ0|y) = 1- PB
PBは、帰無仮説の値を∈最小HPD(最高事後密度)区間によって受け入れられるAUCの補集合である。
もしPBが小さいなら、帰無仮説帰無仮説H0: θ=θ0は事後的に指示されない。
PBをベイズ流のP値とみなすことができる。
クロスオーバー試験:ベイズ流仮説検定における信用区間の利用
収縮期高血圧であるn=30の患者が、2つの降圧治療AとBを無作為に割り付けられた。
一ヶ月の治療後、血圧低下が測定された。無治療期間ののち、治療Aだった患者は治療Bで次の期間治療された。
θをAがBより血圧低下が優れている確率とする。
磁気効果がない場合、H0:θ=θ0(=0.5)を両側2項検定に用いることができる。この結果、AのほうがBより血圧低下が良かったことがわかった(P=0.043)
30人のうち、21人が成功は、β分布Beta(22,10)。θの95%HPD区間は[0.53, 084]であり、0.5を含んでいない。
θ=0.5を含む最小HPD区間はPB=0.0232に対して示される。したがって、帰無仮説には強い疑いがある。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 |
> # cross-over example Chapter 3 > > begin <- 0 > end <- 1 > > x <- seq(begin,end,0.0001) > lx <- length(x) > > > # **************************** > # 95% HPD interval > # **************************** > > hpdbeta <- function(p1=11,q1=21,n=20,x=5) + { + # posterior = prior + likelihood + p2 <- p1+x + q2 <- q1+n-x + + f <- function(x,p=p2,q=q2){b<-qbeta(pbeta(x,p,q)+0.95,p,q);(dbeta(x,p,q)-dbeta(b,p,q))^2} + + hpdmin <- optimize(f,lower=0,upper=qbeta(0.05,p2,q2),p=p2,q=q2)$minimum + hpdmax <- qbeta(pbeta(hpdmin,p2,q2)+0.95,p2,q2) + return(c(hpdmin,hpdmax)) + } > > ncross <- 30 > xcross <- 21 > > hpdcrossover <- hpdbeta(p1=1,q1=1,n=ncross,x=xcross) > > # 95% HPD interval > > hpdcrossover [1] 0.5282884 0.8402629 > > # **************************** > # Contour probability > # **************************** > > p <- xcross+1 > q <- ncross-xcross+1 > > # change appropriately when xcross < ncross/2 > > x05 <- x[x > 0.5] > dx05 <- dbeta(x05,p,q) > > xr05 <- x05[dx05==dx05[(dx05-dbeta(0.5,p,q))^2==min((dx05-dbeta(0.5,p,q))^2)]] > > > # contour probability > > bpval <- pbeta(0.5,p,q)+(1-pbeta(xr05,p,q)) > bpval [1] 0.02307768 > > # plotting the posterior and contour probability > > # determine value in x-series the symmetric x with dbeta closiest to dbeta(0.5,p,q) > # apply when xcross > ncross/2 > > > > # check that chosen value in x-series has beta value close to that of 0.5 > > dbeta(xr05,p,q) [1] 0.4127289 > dbeta(0.5,p,q) [1] 0.4130617 > > # create plot > > # plot works for xcross between 16 and 24 for stepsize in x equal to 0.0001 > # for xcross greater than 24 decrease stepsize further > > par(mfrow=c(1,1)) > par(pty="m") > par(mar=c(5,5,4,2)+0.1) > > dx <- dbeta(x,p,q) > plot(x,dx,xlab=expression(theta),ylab="",lwd=1,col=1,type="n", + bty="l",cex.lab=1.8,cex=1.2,cex.axis=1.5,yaxt="n") > > xleft <- x[x>0 & x < 0.5] > dleft <- dbeta(xleft,p,q) > nleft <- length(xleft) > xleftpol <- c(xleft,xleft[nleft],xleft[1]) > dleftpol <- c(dleft,0,dleft[1]) > polygon(xleftpol,dleftpol, col="light blue", lwd=2, + border="black") > > xright <- x[x>xr05 & x < 0.95] > dright <- dbeta(xright,p,q) > nright <- length(xright) > xrightpol <- c(xright,xright[1],xright[1]) > drightpol <- c(dright,0,dright[1]) > polygon(xrightpol,drightpol, col="light blue", lwd=2, + border="black") > > lines(x,dx,lwd=3,type="l") > segments(0.5,dbeta(0.5,p,q),xr05,dbeta(0.5,p,q)) > segments(0.5,0,xr05,0,lty=1,lwd=5) > text((0.5+xr05)/2,dbeta(0.5,p,q)/3,"smallest HPDI with 0.5",adj=0.5,cex=1.2) > > eps <- 0.01 > > arrows(0.5-eps,1.0,0.5-eps,0.3) > arrows(xr05+eps,1.0,xr05+eps,0.3) > segments(0.5-eps,1.0,xr05+eps,1.0) > text(0.1,0.6*max(dx),expression(paste(p[B], " against ", theta, " = 0.5")), + adj=0,cex=1.7) > arrows(0.12,0.55*max(dx),0.5-eps,1.0) > text(0.49,-0.1,"0.5",adj=0) |
3.8.2 ベイズファクター
仮説を支持する事前から事後へのオッズの変化を測るものであり、ベイズ統計における尤度比検定に相当する。
観察されたデータyが与えられたもとで、特定の仮説Hが真である事後確率をp(H|y)とする。
仮説Hのもとで、θに関する事前確率をp(θ|H)とし、p(y|H)=∫p(y|θ)p(θ|H)dθ。
p(H0|y)>0.5であれば、帰無仮説に対する強い事後信念が与えられて、帰無仮説が選択されることを示している。
Hαは、H0の補集合なので、p(Hα)=1-p(H0), p(Hα|y)=1-p(H0|y)となり、
p(H0|y)/(1-p(H0|y) = p(y|H0)/p(y|Hα)x p(H0)/(1-p(H0))
上記式は、仮説H0に関する事前オッズが、ベイズファクター項p(y|H0)/p(y|Hα)で乗算することにより、事後オッズに代わることを示している。ベイズファクターは仮説H0とHαのもとでの尤度比であり、0〜∞の値をとる。
BF(y)が1より大きい時、H0に関する事後確率は事前確率よりも大きくなる。ベイズファクターは帰無仮説に関係していて、値が小さい時にHαが支持される。
Hαに対してH0を支持:
BF(y) > 100 明白;
32 < BF(y) <= 100 とても強い;
10 < BF(y) <= 32 強い;
3.2 < BF(y) <= 10 かなり;
1 < BF(y) <= 3.2 特筆に値するほどでない;
ーーーーーーーーーーーーーーーーーーーーーーーーー