Bayesian Biostatistics by E Lesaffre & AB Lawson, Chapter 2 学習ノート
———————————————————————
yi(i=1,…,n)はn個の独立な計数データとする。係数データの例としててんかん患者の1ヶ月のてんかん発作回数、ある病院1年での医療ミスの回数、国勢調査地域における疾病数などがある。ポアソン分布は、計数データ分布の記述によく利用されるモデルである。
p(y|θ) = θ^y*e^(-θ)/y!
yiが単位時間などで観察した度数となる。yiが基幹tiで観測された場合、
p(y|θ) = (θti)^y*e^(-θti)/y!
虫歯研究:Flandersにおける虫歯研究 ST研究
4468名の児童が産科。Flandersで1989年に生まれた児童の7%である標本
試験の一年目の7歳の乳歯の虫歯データをみる。乳歯の虫歯は伝統的にdmft指数で測定されている。
腐食したdecayed虫歯が理由で抜歯して歯がなくなったmissing(m),詰め物をしたfilled(f)という乳歯の数である。スコアは0(虫歯なし)から20(すべての乳歯が虫歯)までの値を取る。
4351名の児童のdmft指数データが得られ、そのたの口腔衛生や食事習慣に関しても記録された。
dmft指数が従うポアソン尤度はp(yi|θ)の積であり、以下のようになる。
L(θ|y) = Πp(yi|θ) = Π(θ^yi / yi!)e^(-nθ)
θに関する関数を最大化すれば、θのMLE,θ_MLE = y_barが得られる。θ_MLE = 2,24となる。尤度に基づく95%CIは[2.1984, 2,2875]となる。
<ベイズ流アプローチ>
ST研究に対する事前分布の特定
1983年のLiegeで行った109名の7歳時の試験 dmft指数の平均は4.1
1994年のGhentで行った200名の5歳児の試験 dmft指数の平均値1.39
ポアソン尤度に対する便利な事前分布はガンマ分布であり、Gamma(α, β)とする。
αは形状パラメータで、βは尺度パラメータである。
事前分として、θ~Gamma(α0, β0)、E(θ)=α0/β0、var(θ) = α0/β0^2を仮定する。
α0=3, β0=1のとき、
2. 事後分布の構築
Gamma(α0, β0)事前分布は、θの関数として、
p(θ) = β0^α0 / Γ(α0) * θ(α0-1) * e(-β0*θ)
事後確率密度はL(θ|y)p(θ)に比例する。
p(θ|y) ∝ e(-nθ)Π(θ^yi/yi!)*β0^α0/Γ(α0)*θ(α0-1)*e(-β0*θ)∝ θ^(Σyi+α0)-1 * e(-(n+β0)*θ)
上記は、ガンマ分布Gamma(Σyi+α0-1, n+β0)のカーネル。
次ゴミ確率分布は
p(θ|y) = p(θ|y_bar) = β_bar^α_bar/Γ(α_bar)*θ^(α_bar-1)*e(-β_bar*θ)
ただし、α_bar = Σyi + α0, β_bar = n + β0
データファイルdmft.txtをread()する。
注:フィールド名V1をYに書き換えないと動かない。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 |
> dmft =read.delim("dmft.txt", header=TRUE) > attach(dmft) > objects(2) [1] "Y" > > > dmft <- V1 エラー: オブジェクト 'V1' がありません > > table(dmft)/4351 dmft 0 1 2 3 4 5 0.4396690416 0.1144564468 0.0937715468 0.0756148012 0.0666513445 0.0574580556 6 7 8 9 10 11 0.0489542634 0.0367731556 0.0314870145 0.0153987589 0.0091932889 0.0052861411 12 13 14 16 18 0.0034474833 0.0006894967 0.0004596644 0.0004596644 0.0002298322 > > mdmft <- mean(dmft) 警告メッセージ: mean.default(dmft) で: 引数は数値でも論理値でもありません。NA 値を返します > > n <- length(dmft) > sdmft <- sum(dmft) > > n;sdmft [1] 1 [1] 9758 > > x <- seq(0,18,1) > > dpoisx <- dpois(x,mdmft) > > vbreaks <- seq(-0.00001,19.00001,1) > > hist(dmft,prob=T,xlab="dmft-index",ylab="", + breaks=vbreaks,col="light blue",main="",cex.lab=1.8,cex=1.2,cex.axis=1.3) hist.default(dmft, prob = T, xlab = "dmft-index", ylab = "", でエラー: 'x' は数値でなければなりません > > attach(dmft) 以下のオブジェクトは dmft (pos = 3) からマスクされています: Y > objects(2) [1] "Y" > > > dmft <- Y > > table(dmft)/4351 dmft 0 1 2 3 4 5 0.4396690416 0.1144564468 0.0937715468 0.0756148012 0.0666513445 0.0574580556 6 7 8 9 10 11 0.0489542634 0.0367731556 0.0314870145 0.0153987589 0.0091932889 0.0052861411 12 13 14 16 18 0.0034474833 0.0006894967 0.0004596644 0.0004596644 0.0002298322 > > mdmft <- mean(dmft) > > n <- length(dmft) > sdmft <- sum(dmft) > > n;sdmft [1] 4351 [1] 9758 > > x <- seq(0,18,1) > > dpoisx <- dpois(x,mdmft) > > vbreaks <- seq(-0.00001,19.00001,1) > > hist(dmft,prob=T,xlab="dmft-index",ylab="", + breaks=vbreaks,col="light blue",main="",cex.lab=1.8,cex=1.2,cex.axis=1.3) > > |
α_bar = 9758+3 = 9761, β_bar = 4351 + 1 = 4352となる。つまり、明らかに事前分布の事後分布に対する影響は小さい。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 |
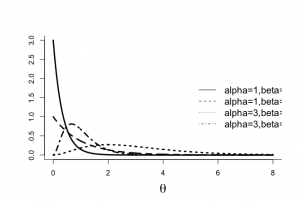
# gamma prior density to STM study par(mfrow=c(1,1)) par(pty="m") par(mar=c(5,5,4,2)+0.1) x <- seq(0,20,0.01) alpha0 <- 3 beta0 <- 1 y <- dgamma(x, shape=alpha0, rate = beta0) plot(x,y,xlab=expression(theta),type="n",ylab="", bty="l",cex.lab=1.8,cex=1.2,cex.axis=1.3) lines(x,y,lwd=3) text(8,0.10,"Gamma(3,1)",cex=1.8) # different gamma densities - extra not in figure 2.11 x <- seq(0,8,0.01) alpha1 <- 1 beta1 <- 3 y <- dgamma(x, shape=alpha1, rate = beta1) plot(x,y,xlab=expression(theta),ylab="",type="n", bty="l",cex.lab=1.8) lines(x,y,lwd=3,lty=1) alpha2 <- 1 beta2 <- 1 y <- dgamma(x, shape=alpha2, rate = beta2) lines(x,y,lwd=3,lty=2) alpha2 <- 3 beta2 <- 1 y <- dgamma(x, shape=alpha2, rate = beta2) lines(x,y,lwd=3,lty=3) alpha2 <- 3 beta2 <- 3 y <- dgamma(x, shape=alpha2, rate = beta2) lines(x,y,lwd=3,lty=4) legend(5,2,c("alpha=1,beta=3", "alpha=1,beta=1", "alpha=3,beta=1", "alpha=3,beta=3"), lty=c(1,2,3,4),cex=1.3,bty="n") |
3. 事後分布の性質
事後分布は以下の性質をもつ。
事後分布は事前分布と尤度関数の妥協compromiseとなる。
背後分布は事前分布と尤度関数より尖っている。
標本サイズが大きいと、尤度が事前分布を支配する
事後分布が事前分布と同じガンマ分布族に属している(共役性)
4. 事前情報と追加データの同等性
スケール化ポアソン尤度(AUC=1)はθの関数として、ガンマ分布Gamma(Σyi+1,n)と等しい。
事前分布Gamma(α0, β0)は大きさβ0, 度数和がα0-1の試験に対応する。
<ベイズ流アプローチ:利用できる事前情報がない場合>
ポアソン分布の平均パラメータに関する事前情報が利用できないとき、α0=1, β0=0が尤度にほとんど事前データがないことを示唆している。
ポアソン分布の度数とは、平均で一定数に発生する独立なイベントの合計数である。同じ口の中の虫歯はには相関が有り、ポアソン課分散、すなわち分散が平均よりずっと大きくなるという減少をもたらす。ここでは、var(dmft)/mean(dmft) = 3.53となる。