ベイズ定理：事後分布の計算　二項分布の場合

Published on by anesth

Bayesian Biostatistics by E Lesaffre & AB Lawson, Chapter 2 学習ノート
——————————————-
2.1　はじめに
2.2 ベイズの定理：2値の場合
ベイズの定理を統計モデルに適用する。
疾病の有無D+, D-をバラメータθ=1, θ=0と対比させる。
また診断結果陽性T+, 陰性T-をy=0, y=1と記録する。

すると、ベイズの展開定理により、
P(θ=1|y=1) = p(y=1|θ=1)p(θ=1)/(p(y=1|θ=1)p(θ=1)+p(y=1|θ=0)p(θ=0)

つまり、
p(D+|T+) = p(T+|D+)p(D+)/(p(T+|D+)p(D+)+p(T+|D-)p(D-)

p(θ=1)、つまりP(D+) は、有病率であり、これはθ=1の事前確率。
(p(y=1|θ=1)は、疾病ありD+の場合の診断結果の陽性率。
p(θ=1|y=1)は、診断陽性の人の有病率で、事後分布と呼ばれる。

簡単には、
p(θ|y) = p(y|θ)p(θ) / p(y)

2.3 ベイズ統計学における確率
この章では、ベイズ統計学の大きな特徴である主観確率というものについて述べている。
理解する上で、困難な点はない。

2.4 ベイズの定理：離散値の場合
被験者がK(>2)の診断クラスに属しているとする。K(>2)個の診断クラスは、θのK個の値θ1,…θkに対応し、yがL個の値y1,…yLを取るとすると、ベイズの定理は、
p(θk|y) = p(y|θk)p(θk)/(Σp(y|θm)p(θm))
と一般化される。ただし、yはL個の取りうる値の一つである。
この場合、θは離散型、yは、離散型でも連続型でもよい。

2.5 ベイズの定理：連続値の場合
この場合には、p(y|θ）は確率関数、もしくは確率密度関数を表す。ベイズ統計において、パラメータは確率変数である。yは、同一の分布からのn個の観測値の標本を表す。この標本の同時分布はp(y|θ）=Πp(yi|θ）で与えられ、L(θ|y)とも表せる。

連続型パラメータに対するベイズの定理は、
p(θ|y) = L(θ|y)p(θ)/p(y) = L(θ|y)p(θ)/∫L(θ|y)p(θ)dθ
分母は平均尤度averaged likelihoodと呼ばれる。

事後分布が尤度と事前分布の積に比例していることは、
p(θ|y) ∝ L(θ|y)p(θ)　となる。

2.6 二項分布の場合
データが離散型で、パラメータが連続型のベイズ定理の構造。

脳卒中試験：虚血性脳卒中に投与される血栓溶解剤の安全性モニタリング調査。
遺伝子組換え組織プラスミノーゲン活性化因子（rt-PA)は、プラセボ対照ランダム化比較試験ECASS 1試験と、ECASS 2試験で期待できる結果が得られている。
一方で、すべての血栓溶解剤に対して、重要な出血性合併症は神経機能の低下に伴う大脳内の出血と定義された症候性脳内出血（symptomatic intercerebral hemorrhage, SICH)である。
ECASS 3試験では、症状が発症してから3〜4.5時間以内にrt-PAを投与された急性虚血性脳卒中患者での有効性と安全性の検証試験:
821名が登録: rt-PA 481名、プラセボ403名。結果は、統計学的に有意（p=0.04)で、rt-PAがプラセボ群よりも多く、患者で良好な結果（90日無害）を得た。

治療の安全性は、データ安全性モニタリング委員会(data and safety monitoring board, DSMB)と呼ばれ、定期的に試験をモニタリングする。

ECASS 3試験において、SICHの発生率をモニタリングすることが必要となった。この場合、
1) ECASS 1とECASS 2からの事前データがある。
2) 他の試験からSICHに対するメタアナリシスで事前情報が得られた。

ECASS 2では、rt-PAを受けた100例において、SICHの発生率は8名であった。
ECASS 3中間報告では、rt-PA治療を受けた50名のうち、10名でSICHが発生した。
そこで、この試験を継続するか中止するかの決定は、ECASS 2とECASS 3中間報告を結合して行う。

rt-PA治療を受けた後のSICHの発生率をθとする。y1,.y2,….,ynはn個の独立な同一分布からのベルヌーイ確率からなる標本で、i番目の患者にSICHが発生すればyi=1、発生しなければyi=0となる。
従って、確率変数 y=Σyiは、2高分布Bin(n,θ)に従い、その確率関数はp(y|θ）= (n y)θ^y * (1-θ)^(n-y)となる。

＜尤度論的アプローチと頻度論的アプローチ＞
ECASS 3試験中間解析におけるSICHの発生率の最尤推定値（MLE）をθ_MLEとした場合、y/n=10/50=0.20となる。


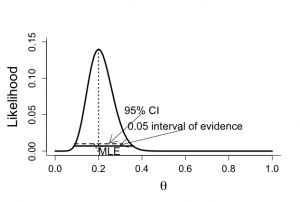
0.05 Interval of evidence、すなわち少なくとも0.05の標準化尤度をもつようなパラメータθの区間は、[0.09, 0.36]
頻度論的アプローチでは、2項検定またはZ検定を用いてθ=0.08かどうかという仮説を検定する。
ここでの値0.08はｍECASS 2の試験結果から得られたものである。漸近正規分布に基づくθ_MLEの古典的95%信頼区間は[0.089, 0,31]となる。

＜ベイズ流アプローチ＞
1. ECASS 2試験からの事前分布の特定
rt-PA群の100名(=n0)中、SICHが発症したのは8名(=y0)であった。
対応する尤度は、L(θ|y0) = (n0, y0)*θ^y0*(1-θ)^(n0-y0)
θの尤もらしい値として、 θ_MLE0 = y0/n0 = 0.08が得られる。
このことは、ECASs 2試験の結果が区間[0.02, 0.18]外のSICH発生率を指示していないことを示す。

そこで、ECASS 2の尤度は、ECASS 3試験におけるθに関する事前信念として利用する。
θの関数としての尤度関数は、L(θ|y0)=の曲線下面積（AUC)が1でないために分布ではない。
ここを1とするためには、∫L(θ|y0)dθ = aとすると、p(θ)=L(θ|y0)/aは事前分布としての条件を満たす。（このあたりの日本語訳は怪しげ。ちょっと原著を調べる必要あり）

ECASS 2試験における２項尤度のカーネルはθ^y0*(1-θ)^(n0-y0)は、定数を除けばベータ密度(beta density)の表現となる。
p(θ) = 1/B(α0, β0) * θ^(α0-1) * (1-θ)^(β0-1)

ただし、B(α, β) = Γ(α)Γ(β)/Γ(α+β) = ∫θ^(α-1) * (1-θ)^(β-1)dθ

注意：ここでは、B(α, β)はβ関数で、Beta()はβ分布

β分布=1/β関数 * 尤度カーネル

そこでαをy0-1、βをn0-y0+1で置き換えればECASS 2試験の尤度は定数を除いて得られる。

要するに事前分布の尤度をθの分布へ変えるのには、2項係数の代わりに、1/B(α0, β0) を利用する。
ここでは、rt-PA群の100名(=n0)中、SICHが発症したのは8名(=y0)であったので、
β分布は、α0=8+1=9、β0=100-8+1=93となる。

β分布　Beta(α, β)は区間[0, 1]で定義されている分布族である。

2. 事後分布の構築
このStudyをベイズの定理
p(θ|y) = L(θ|y)p(θ)/p(y) = L(θ|y)p(θ)/∫L(θ|y)p(θ)dθ
に、適応させるためには、
a) 事前分布：ECASS 2試験から得られるデータ
b) 尤度L(θ|y): ECASS 3試験中間データから得られた解析結果(y=10, n=50)
c) 平均尤度　∫ L(θ|y)p(θ)dθ

ベイズの定理の分子は、事前分布と尤度の積

L(θ|y)p(θ) = (n y) * 1/B(α0,β0)*θ^(α+y-1) * (1-θ)^(β0+n-y-1)

平均尤度∫ L(θ|y)p(θ)dθは、θ^(α+y-1) * (1-θ)^(β0+n-y-1)が、パラメータα0+yとβ0+n-yをもつβ分布のカーネルであるので、
p(y) = (n y) * B(α0+y, β0+n-y)/B(α0, β0)

p(θ|y) = (n y) * 1/B(α0,β0)*θ^(α+y-1) * (1-θ)^(β0+n-y-1) ÷　 (n y) * B(α0+y, β0+n-y)/B(α0, β0)

= 1/B(α0,β0)*θ^(α+y-1) * (1-θ)^(β0+n-y-1) ? B(α0, β0) / B(α0+y, β0+n-y)

= 1/ B(α0+y, β0+n-y) * θ^(α+y-1) * (1-θ)^(β0+n-y-1)

= 1/ B(α_bar, β_bar) * θ^(α_bar-1) * (1-θ)^(β_bar-1)

ここでα_bar = α0 + y, β_bar = β0 + n – y

事後分布は、再びβ分布(α_bar, β_bar)に対応する。
ECASS 2では、rt-PAを受けたn0=100例において、SICHの発生率はy0=8名であった。
ECASS 3中間報告では、rt-PA治療を受けたn=50名のうち、y=10名でSICHが発生した。
事前のβ分布は、α0=8+1=9、β0=100-8+1=93であったので、

α_bar = α0 + y = 9 + 10 、β_bar = β0 + n – y = 93 + 50 – 10 = 133
となり、
α_bar = 19, β_bar = 133

これでECASS 3試験の中間解析に対して、ベータ事前分布、2項尤度（AUC=1にスケール化）とベータ事後分布が得られた。

3. 事後分布の性質
事前分布を最大化させる値θ0= y0/n0
尤度に関して最尤推定値 θ_MLE = y/n
事後分布を最大化させる値θ_M = (α_bar -1)/(α_bar + β_bar – 2) = (y + y0)/(n + n0)

ECASS 2では、rt-PAを受けたn0=100例において、SICHの発生率はy0=8名であった。
ECASS 3中間報告では、rt-PA治療を受けたn=50名のうち、y=10名でSICHが発生した。

θ_M = y/(n + n0) + y0/(n + n0)
= n0*θ0 / (n0 + n) + n*θ_MLE /(n0 + n)
= 100 * 0.08 /150 + 50 * 0.2 / 150
= 0.053333 + 0.08
= 0.133333
となる。つまり、事後分布の尤もな値は、事前分布の尤もな値とデータから計算した尤もの値の重み付き平均となる。

α_bar = α0 + y, β_bar = β0 + n – y の式から、試験のサイズ(nとy)が増加すれば、事前パラメータ（α0、β0）の事後分布に対する影響が減少することがわかる。「大標本では、尤度が事前分布を支配する」ことを意味する。

事後分布が事前分布と同じベータ分布であった。この性質は共役conjugacyと呼ばれる。

θに対する事後の最大値は、(y + y0)/(n + n0)であり、これはECASS 2試験と、ECASS 3試験のデータを併合した場合の最尤推定値である。これは、 ECASS 2試験と、ECASS 3試験の実施条件が同じという暗黙の仮定にもとづいている。このことは、過去と現在のデータが交換可能であることを仮定している。

4. 事前情報と追加データの同等性
事前分布のBeta(α、β)は、α+β-2回試行中α-1回成功する二項試行と同じである。
さらにスケール尤度は分布Beta(y+1, n-y+1)と等しく、事前分布Beta(α0, β0)をデータに追加すると、分布Beta(α0+y, β0+n-y)が導かれる。
簡単に言えば、観察データに対して、α0-1回成功、β0-1回失敗という別のデータを追加することと同等である。

ベイズ流アプローチ：主観事前分布

ECASS 3試験開始時に、DSMBはSICHの発生率が5%-20%の間にあると考えていた。
たとえば、ECASS 3試験対象者がECASS 2対象者より5歳年上であったとした場合、事前分布にECASS 2の試験結果だけでなく、事前の信念を調整することもある。

ベイズ流アプローチ：利用できる事前情報がない場合
無情報事前分布(non-informative, NI)
よく用いられる無情報事前分布に一様分布があり、フラット事前分布（flat prior distribution)と呼ばれる。

ここでは、一様分布はパラメータα=β=1をもつβ分布である。