二項分布
pk = nCk * p^k * (1-p)^(n-k)
で、np=λ を一定に保って、p -> 0, n ->∞の極限を取ると、
ポアソン分布 pk = λ^k / k! * exp(-λ)
となる。
二項分布の平均np、分散はnp(1-p)であったが、ポアソン分布では、平均がnp=λ、分散もnp(1-p)->np=λとなる。
Rには平均λのポアソン分布の
確率 dpois(x, λ)
分布関数 ppois(q, λ) = Σdpois(x, λ)
分位関数 qpois(p, λ)
乱数をn個発生するrpois(n, λ)
|
1 2 3 4 5 6 |
> plot(c(0,1200), c(0,3), type="n", axes=FALSE, xlab="", ylab="") > axis(1) > r1 = runif(17) * 1200 > r2 = runif(38) * 1200 > segments(r1, 0.5, r1, 1.5) > segments(r2, 2, r2, 3) |
|
1 |
> stripchart(sample(1:50, 500, replace=TRUE), pch=15, method="stack", axes=FALSE, at=0) |

λ=10のポアソン分布の分散はλ=10なので、標準偏差は√10k
|
1 2 |
> sum(10^(7:13)* exp(-10) / factorial(7:13)) [1] 0.734323 |
あるいは、
|
1 2 |
> ppois(13, 10) - ppois(6, 10) [1] 0.734323 |
平均値λのポアソン分布の信頼区間は、
|
1 2 3 4 5 6 7 8 9 10 11 12 |
> poisson.test(10) Exact Poisson test data: 10 time base: 1 number of events = 10, time base = 1, p-value = 1.114e-07 alternative hypothesis: true event rate is not equal to 1 95 percent confidence interval: 4.795389 18.390356 sample estimates: event rate 10 |
で[4.8, 18,4]であることがわかる。
|
1 2 3 4 5 6 7 8 9 10 11 12 |
> poisson.test(10, conf.level=0.6826895) Exact Poisson test data: 10 time base: 1 number of events = 10, time base = 1, p-value = 1.114e-07 alternative hypothesis: true event rate is not equal to 1 68.26895 percent confidence interval: 6.891306 14.266950 sample estimates: event rate 10 |
0回しか起きなかった68%信頼区間は、0ではなく、[0, 1.84]となる。
|
1 2 3 4 5 6 7 8 9 10 11 12 |
> poisson.test(0, conf.level=0.6826895) Exact Poisson test data: 0 time base: 1 number of events = 0, time base = 1, p-value = 1 alternative hypothesis: true event rate is not equal to 1 68.26895 percent confidence interval: 0.000000 1.841022 sample estimates: event rate 0 |
0回しか起きなかっと場合のλの95%信頼区間は[0, 3.7]となる。
|
1 2 3 4 5 6 7 8 9 10 11 12 |
> poisson.test(0) Exact Poisson test data: 0 time base: 1 number of events = 0, time base = 1, p-value = 1 alternative hypothesis: true event rate is not equal to 1 95 percent confidence interval: 0.000000 3.688879 sample estimates: event rate 0 |
バックグラウンドのある場合のポアソン分布
約99.7%の確率でもっと、バックグラウンドの信号分布に被測定物質が検出されない最低量(平均+3σ)が検出限界として定義されている。
二項分布として考えれば、仮にバックグラウンドb=0だとすると、検出限界を3σとすれば
|
1 2 |
> pnorm(-3) [1] 0.001349898 |
この0,00135は、(1/2)^10強
|
1 2 3 4 |
> (1/2)^10 [1] 0.0009765625 > (1/2)^9 [1] 0.001953125 |
つまりs=10ならこの確率より小さくなる。
3σ相当の両側確率は、pnorm(-3)*2=0,0027なので、
> binom.test(100, 249, 0.5)$p.value
[1] 0.002285436
> binom.test(100, 248, 0.5)$p.value
[1] 0.002766705
で全部で249カウント、つまり試料が149カウントであればよい。
ガイガーカウンタとポアソン分布
μSc/h単位で測定した放射線の強さ(確率変数)をX、cpm(μS/h)単位の感度をs、測定時間をm分とすると、m分のカウント数は、msXであり、ポアソン分布の性質E(msX) = V(msX)から、
msE(X) = m^2s^2V(X)
s=E(X)/mV(X)
ポアソン分布の信頼区間
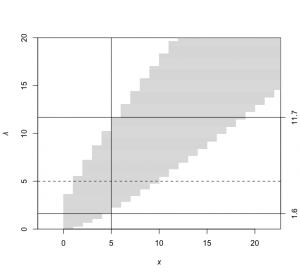
ポアソン分布に従う事象がx=5回起こった場合のパラメータλの95%信頼区間は、
|
1 2 3 4 5 6 7 8 9 10 11 12 |
> poisson.test(5) Exact Poisson test data: 5 time base: 1 number of events = 5, time base = 1, p-value = 0.00366 alternative hypothesis: true event rate is not equal to 1 95 percent confidence interval: 1.623486 11.668332 sample estimates: event rate 5 |
95%信頼区間[1.623486, 11.668332]
|
1 2 3 4 |
> 1 - ppois(4, 1.623486) [1] 0.02499998 > ppois(5, 11.668332) [1] 0.025 |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
> poisson.test(5, r=1.623486, alternative="greater") Exact Poisson test data: 5 time base: 1 number of events = 5, time base = 1, p-value = 0.025 alternative hypothesis: true event rate is greater than 1.623486 95 percent confidence interval: 1.97015 Inf sample estimates: event rate 5 > poisson.test(5, r=11.668332, alternative="less") Exact Poisson test data: 5 time base: 1 number of events = 5, time base = 1, p-value = 0.025 alternative hypothesis: true event rate is less than 11.66833 95 percent confidence interval: 0.00000 10.51303 sample estimates: event rate 5 |
|
1 2 3 4 5 6 7 8 9 10 11 |
> plot(NULL, xlim=c(0,20), ylim=c(0,20), xaxs="i", yaxs="i", asp=1, + xlab=expression(italic(x)), ylab=expression(italic(λ))) > for (lambda in seq(0,20,0.1)) { + x = qpois(c(0.025,0.975), lambda) + segments(x[1], lambda, x[2], lambda, col="gray") + } > abline(v=5) > abline(h=1.623486) > abline(h=11.668332) > abline(h=5, lty=2) > axis(4, c(1.623486,11.668332), labels=c(1.6,11.7)) |
|
1 2 3 4 5 6 7 8 9 10 11 12 |
> poisson.test(7, r=3) Exact Poisson test data: 7 time base: 1 number of events = 7, time base = 1, p-value = 0.03351 alternative hypothesis: true event rate is not equal to 3 95 percent confidence interval: 2.814363 14.422675 sample estimates: event rate 7 |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
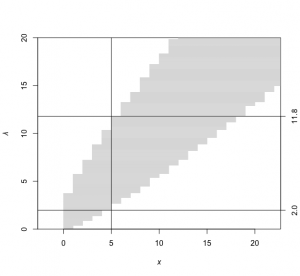
> plot(NULL, xlim=c(0,20), ylim=c(0,20), xaxs="i", yaxs="i", asp=1, + xlab=expression(italic(x)), ylab=expression(italic(λ))) > for (lambda in seq(0,20,0.1)) { + t = sort(dpois(0:100, lambda), decreasing=TRUE) + s = cumsum(t) + m = t[sum(s < 0.95) + 1] + x = range((0:100)[dpois(0:100, lambda) >= m]) + segments(x[1], lambda, x[2], lambda, col="gray") + } > abline(v=5) > abline(h=1.9701) > abline(h=11.7992) > axis(4, c(1.9701,11.7992), labels=c("2.0","11.8")) |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
> library(exactci) > poisson.exact(7, r=3, tsmethod="minlike") Exact two-sided Poisson test (sum of minimum likelihood method) data: 7 time base: 1 number of events = 7, time base = 1, p-value = 0.03351 alternative hypothesis: true event rate is not equal to 3 95 percent confidence interval: 3.2853 14.3402 sample estimates: event rate 7 |