ここまで強引に統計の基本をすっ飛ばして来たが、一度Rと統計の基本を確認しておく。
———————————————–
Rで楽しむ統計(奥村晴彦著、共立出版)からの学習ノート
———————————————–
一様乱数(uniform random numbers): runif(n)関数は、0<=x<1の範囲の一様乱数をn個取り出す。
|
1 2 3 4 5 |
> runif(1) [1] 0.6177708 > runif(10) [1] 0.70371545 0.08929393 0.07095331 0.87560553 0.21531889 0.82794357 [7] 0.66564415 0.17376897 0.79990573 0.62729060 |
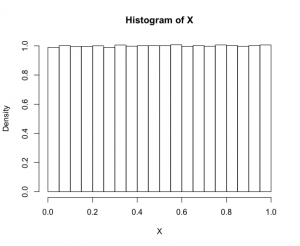
百万個取り出せば、
|
1 2 |
> X=runif(1000000) > hist(X, freq=FALSE) |
|
1 |
> hist(X, freq=FALSE, col="gray", breaks=50) |

ヒストグラムを関数で表したものを確率密度関数(probability density function、略してpdf)、または密度関数と呼ぶ。
任意のa
> hist(X, freq=FALSE)
3つ加えると、
> X=runif(1000000) + runif(1000000) + runif(1000000)
> hist(X, freq=FALSE)

runif()は平均値が0.5である。そこで、0.5を引いて範囲を-0.5<=x<0.5とすれば、 分散は、∫x^2dx = 1/12 であるので、ちょうど12個加えると分散がほぼ1となる。
|
1 2 3 4 5 6 7 8 9 10 11 12 |
> X=runif(1000000) > var(X) [1] 0.08330094 > X=runif(1000000) + runif(1000000) > var(X) [1] 0.1666514 > X=runif(1000000) + runif(1000000) + runif(1000000) > var(X) [1] 0.2508489 > X=runif(1000000) + runif(1000000) + runif(1000000)+ runif(1000000) + runif(1000000)+ runif(1000000) + runif(1000000)+ runif(1000000) + runif(1000000)+ runif(1000000) + runif(1000000)+ runif(1000000) + runif(1000000) > var(X) [1] 1.083516 |
|
1 2 3 4 5 6 7 8 9 10 11 12 |
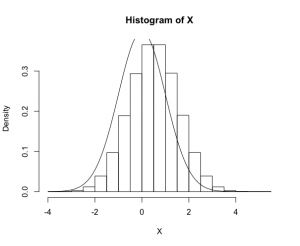
> X=runif(1000000) + runif(1000000) + runif(1000000)+ runif(1000000) + runif(1000000)+ runif(1000000) + runif(1000000)+ runif(1000000) + runif(1000000)+ runif(1000000) + runif(1000000)+ runif(1000000) + runif(1000000) > hist(X, freq=FALSE) > hist(X, freq=FALSE, col="gray", breaks=50) <a href="http://anesth-kpum.org/blog_ts/wp-content/uploads/2018/02/Rplot15.png"><img src="http://anesth-kpum.org/blog_ts/wp-content/uploads/2018/02/Rplot15-300x246.png" alt="" width="300" height="246" class="alignnone size-medium wp-image-1205" /></a> > X=runif(1000000) + runif(1000000) + runif(1000000)+ runif(1000000) + runif(1000000)+ runif(1000000) + runif(1000000)+ runif(1000000) + runif(1000000)+ runif(1000000) + runif(1000000)+ runif(1000000) + runif(1000000)-6 > hist(X, freq=FALSE) なめらかな曲線でトレースすると 標準正規分布standard normal distribution: f(x) = 1/ √(2π)exp(-x^2/2) > curve(dnorm(x),add=TRUE) |
|
1 2 3 4 |
> integrate(function(x)(exp(-x^2/2)), -Inf, +Inf) 2.506628 with absolute error < 0.00023 > sqrt(2*pi) [1] 2.506628 |
数学的には、平均値μ、分散σ^2の確率変数がどんな分布であっても、そこから引き出した数X1, X2, …Xnの平均値 X_mean = (X1+X2+…Xn)/nの分布は、平均値がもとと同じのμで、分散がσ^2/nとなるので、
(X_mean- μ)/√σ^2/n の分布は平均値0, 分散1となる。ここでnが十分大きくなると、分布は標準正規分布に近づく。このことが中心極限定理central limit theoremである。
Xが標準正規分布N(0,1)に従うならばσX+μは平均μ、分散σ^2の正規分布(ガウス分布) N(μ, σ^2)に従う。
N(μ, σ^2)の確率密度関数は、f(x) = 1/√(1πσ^2)exp(-(x−μ)^2/2σ^2)
変数がある範囲に入る確率を求めるには、密度関数f(x)を積分して、
累積分布関数(分布関数) F(q) = ∫f(x)dx, -∞-q)
あるいは、左右対称であることから、
つまりほぼ68%の確率で正規分布はμ±σの範囲に入る。
同様にして、μ±2σ、μ±3σに入る確率は、
逆に、μ±kσの範囲に入る確率が95%、99%になるようなkは、
その他の分布
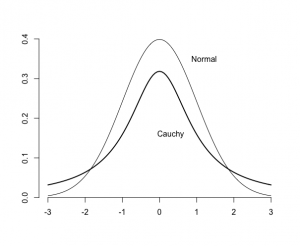
コーシー分布 正規分布に比べて外れ値(outlier)が多い場合の分布のモデルに使われることがある。 カイ二乗分布 v個の数値X1,X2,…..Xv が標準正規分布N(0.1)に従う時、 密度関数 dchisq(x, v) 数値X1,X2,…..Xv が正規分布N(μ, σ^2)に従う時、標本分散 t分布 密度関数dt(x, v) F分布 u1が自由度v1のχ^2分布, u2が自由度v2のχ^2分布に従うとき、 F = (u1/v1) / (u2/v2) を自由度(v1, v2)のF分布に従う。 密度関数 df(x, v1, v2)
を求める。
確率変数Xが a
密度関数が1/(1+ax^2)に比例するコーシー分布(Cauchy distribution)は。中心極限定理が満たされない。
X^2 = X1^2 + X2^2 +….+Xv^2
を自由度vのカイ二乗分布chi-square distribution with v degrees of freedom
分布関数 pchisq(q, v) = ∫dchisq(x,v)dx
分位関数 qchisq(p, v)
乱数をn個発生するrchisq(n,v)
s^2 = 1/(n-1) Σ(Xi-X_mean)^2 の分布はχ^2分布である。
Xが正規分布N(0,1)に従い、Yが自由度vのχ^2分布に従う時
t=χ/√Y/v
は、自由度vのスチューデントのt分布と呼ぶ。
分布関数pt(q, v) = ∫ dt(x, v)dx、-∞〜q)
分位関数 qt(p, v)
乱数n個を発生するrt(n, v)
特に、X1, X2, ..,Xn, Y1, Y2,…., YmがN(μ,σ^2)に従う時、X1, X2, ..,Xnの標本分布をs1^2,Y1, Y2,…., Ymの標本分布をs2^2とすれば、
F = s1^2 / s2^2
は自由度(v1, v2)のF分布に従う。
分布関数 pf(q, v1, v2) =∫(df(x, v1m v2)dx, 0〜1)
分位関数 qf(p, v1, v2)
乱数をn個発生するrf(n, v1, v2)