BPA: ポアソンGLM 第4章 その2
BPA BUGSで学ぶ階層モデリング Baysian Population Analysis Using WinBUGS, Marc Kery & Michael Schaubの学習ノート
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
時間i 空間jで得られたCi,jを年の3次多項式関数モデルとする。期待計数値λi,jのポアソン分布を仮定する。
Ci,j ~ Poisson(λi,j)
対数リンク関数
log(λi,j) = αj + ?βp * Xi^p + εi
αj ~ Normal(μ, σα^2)
εi ~ Normal(0, σε^2)
平均サイト効果μを全体の切片とすると
この場合、サイト効果の分布は、平均μではなく0の正規分布となる
log(λi,j) = μ + ?βp * Xi^p + αj + εi
αj ~ Normal(0, σα^2)
εi ~ Normal(0, σε^2)
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 |
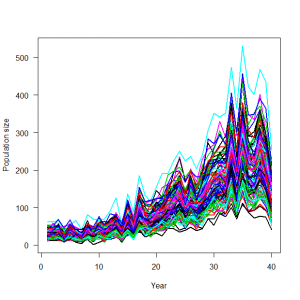
> # 4.3. Mixed models with random effects for variability among groups (site and year effects) > # 4.3.1. Generation and analysis of simulated data > data.fn <- function(nsite = 5, nyear = 40, alpha = 4.18456, beta1 = 1.90672, beta2 = 0.10852, beta3 = -1.17121, sd.site = 0.5, sd.year = 0.2){ + # nsite: Number of populations + # nyear: Number of years + # alpha, beta1, beta2, beta3: cubic polynomial coefficients of year + # sd.site: standard deviation of the normal distribution assumed for the population intercepts alpha + # sd.year: standard deviation of the normal distribution assumed for the year effects + # We standardize the year covariate so that it runs from about 1 to 1 + + # Generate data structure to hold counts and log(lambda) + C <- log.expected.count <- array(NA, dim = c(nyear, nsite)) + + # Generate covariate values + year <- 1:nyear + yr <- (year-20)/20 # Standardize + site <- 1:nsite + + # Draw two sets of random effects from their respective distribution + alpha.site <- rnorm(n = nsite, mean = alpha, sd = sd.site) + eps.year <- rnorm(n = nyear, mean = 0, sd = sd.year) + + # Loop over populations + for (j in 1:nsite){ + # Signal (plus first level of noise): build up systematic part of the GLM including random site and year effects + log.expected.count[,j] <- alpha.site[j] + beta1 * yr + beta2 * yr^2 + beta3 * yr^3 + eps.year + expected.count <- exp(log.expected.count[,j]) + + # Second level of noise: generate random part of the GLM: Poisson noise around expected counts + C[,j] <- rpois(n = nyear, lambda = expected.count) + } + + # Plot simulated data + matplot(year, C, type = "l", lty = 1, lwd = 2, main = "", las = 1, ylab = "Population size", xlab = "Year") + + return(list(nsite = nsite, nyear = nyear, alpha.site = alpha.site, beta1 = beta1, beta2 = beta2, beta3 = beta3, year = year, sd.site = sd.site, sd.year = sd.year, expected.count = expected.count, C = C)) + } > data <- data.fn(nsite = 100, nyear = 40, sd.site = 0.3, sd.year = 0.2) |
winBUGSを使うと、
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 |
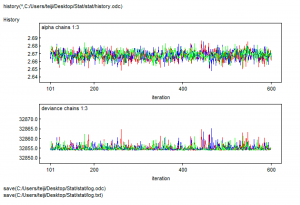
> # Specify model in BUGS language > sink("GLMM_Poisson.txt") > cat(" + model { + + # Priors + for (j in 1:nsite){ + alpha[j] ~ dnorm(mu, tau.alpha) # 4. Random site effects + } + mu ~ dnorm(0, 0.01) # Hyperparameter 1 + tau.alpha <- 1 / (sd.alpha*sd.alpha) # Hyperparameter 2 + sd.alpha ~ dunif(0, 2) + for (p in 1:3){ + beta[p] ~ dnorm(0, 0.01) + } + + tau.year <- 1 / (sd.year*sd.year) + sd.year ~ dunif(0, 1) # Hyperparameter 3 + + # Likelihood + for (i in 1:nyear){ + eps[i] ~ dnorm(0, tau.year) # 4. Random year effects + for (j in 1:nsite){ + C[i,j] ~ dpois(lambda[i,j]) # 1. Distribution for random part + lambda[i,j] <- exp(log.lambda[i,j]) # 2. Link function + log.lambda[i,j] <- alpha[j] + beta[1] * year[i] + beta[2] * pow(year[i],2) + beta[3] * pow(year[i],3) + eps[i] # 3. Linear predictor including random site and random year effects + } #j + } #i + } + ",fill = TRUE) > sink() > > > # Bundle data > win.data <- list(C = data$C, nsite = ncol(data$C), nyear = nrow(data$C), year = (data$year-20) / 20) # Note year standardized > > # Initial values > inits <- function() list(mu = runif(1, 0, 2), alpha = runif(data$nsite, -1, 1), beta = runif(3, -1, 1), sd.alpha = runif(1, 0, 0.1), sd.year = runif(1, 0, 0.1)) > > # Parameters monitored (may want to add "lambda") > params <- c("mu", "alpha", "beta", "sd.alpha", "sd.year") > > # MCMC settings (may have to adapt) > ni <- 100000 > nt <- 50 > nb <- 50000 > nc <- 3 > > # Call WinBUGS from R (BRT 98 min) > out <- bugs(win.data, inits, params, "GLMM_Poisson.txt", n.chains = nc, + n.thin = nt, n.iter = ni, n.burnin = nb, debug = TRUE, bugs.directory = bugs.dir, working.directory = getwd()) Error in bugs.run(n.burnin, bugs.directory, WINE = WINE, useWINE = useWINE, : Look at the log file and try again with 'debug=TRUE' to figure out what went wrong within Bugs. > > # Summarize posteriors > print(out, dig = 3) |
途中でハング!
4.3.2 実際のデータセット解析
1999年からのスイス繁殖鳥類調査MHBのデータ解析。
サイト、年ごとの推定なわばり数の計数値データ:235サイトで9年間に得られたデータの一部。ヒガラの年ごとのなわばり数をモデル化する。解析の目的は、ヒガラ個体群の増減の傾向、サイト・年・観測者の間で計数値データが得られている。
固定効果モデルとランダム効果モデルを比較することでランダム効果への理解を深める。
Ci,j ~ Poisson(λi,j) #データの分布
log(λi,j) = αj + β1 * 年i + β2 * Fi,j + δi + γk(i,j) #リンク関数と線形予測子
αj ~ Normal(μ, σα^2) #ランダムサイト効果
δi ~ Normal(0, σδ^2) #ランダム効果年
γk(i,j) ~ Normal(0,σγ^2) #ランダム観察者効果
Fi,j: 観測者が初めてサイトを調査したことを表す指標変数
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 |
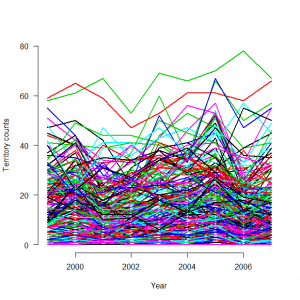
> # 4.3.2. Analysis of real data set > # Read in the tit data and have a look at them #ヒガラのデータの読み込みと概観 > tits <- read.table("tits.txt", header = TRUE) > str(tits) 'data.frame': 235 obs. of 31 variables: $ site : Factor w/ 235 levels "100.1","102.1",..: 36 194 42 37 38 166 39 172 40 41 ... $ spec : Factor w/ 1 level "Coaltit": 1 1 1 1 1 1 1 1 1 1 ... $ elevation: int 420 450 1050 920 1110 510 800 630 590 530 ...#標高 $ forest : int 3 21 32 9 35 2 6 60 5 13 ... #森林被覆 <strong> $ y1999 : int 0 0 NA 11 27 NA 0 14 2 7 ...#なわばり数 $ y2000 : int 1 0 7 9 24 0 6 15 3 5 ... $ y2001 : int 2 0 15 5 21 2 NA 17 2 2 ... $ y2002 : int 2 0 19 9 19 1 NA 6 1 3 ... $ y2003 : int 0 3 12 8 22 0 1 20 NA 3 ... $ y2004 : int 0 2 11 7 31 0 1 16 0 9 ... $ y2005 : int 2 0 12 9 28 0 7 24 1 10 ... $ y2006 : int 1 1 11 6 9 0 1 15 0 9 ... $ y2007 : int 0 0 7 2 18 0 0 9 1 4 ...</strong> $ obs1999 : int 1576 NA NA 1576 1976 NA 3046 3046 245 2095 ...#観測者コード $ obs2000 : int 1576 NA 2064 2031 1976 2158 2158 3046 245 2095 ... $ obs2001 : int 1576 NA 2064 2031 1976 3288 NA 3046 2064 2095 ... $ obs2002 : int 1576 NA 2064 2031 1976 3288 NA 3046 2064 2095 ... $ obs2003 : int 1576 NA 3299 2031 1976 3304 2148 2148 NA 2095 ... $ obs2004 : int 1576 NA 3299 2031 1976 3304 1971 2148 1699 2095 ... $ obs2005 : int 1576 NA 3299 2031 1976 3304 2049 2148 1699 2095 ... $ obs2006 : int 1576 NA 3299 2031 1976 3304 1699 2148 2261 2095 ... $ obs2007 : int 2125 NA 3299 169 1976 3304 1699 2148 2261 2095 ... $ first1999: int 1 NA NA 1 1 NA 1 1 1 1 ...#指標変数一式 $ first2000: int 0 NA 1 1 0 1 1 0 0 0 ... $ first2001: int 0 NA 0 0 0 1 NA 0 1 0 ... $ first2002: int 0 NA 0 0 0 0 NA 0 0 0 ... $ first2003: int 0 NA 1 0 0 1 1 1 NA 0 ... $ first2004: int 0 NA 0 0 0 0 1 0 1 0 ... $ first2005: int 0 NA 0 0 0 0 1 0 0 0 ... $ first2006: int 0 NA 0 0 0 0 1 0 1 0 ... $ first2007: int 1 NA 0 1 0 0 0 0 0 0 ... > C <- as.matrix(tits[5:13]) > obs <- as.matrix(tits[14:22]) > first <- as.matrix(tits[23:31]) > matplot(1999:2007, t(C), type = "l", lty = 1, lwd = 2, main = "", las = 1, ylab = "Territory counts", xlab = "Year", ylim = c(0, 80), frame = FALSE) |
ベクトル変数Cには、as.matrix(tits[5:13])により、上記行列から5行?13行の年ごとの計測数情報が観測者ごとにまとめられている
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
> C y1999 y2000 y2001 y2002 y2003 y2004 y2005 y2006 y2007 [1,] 0 1 2 2 0 0 2 1 0 [2,] 0 0 0 0 3 2 0 1 0 [3,] NA 7 15 19 12 11 12 11 7 [4,] 11 9 5 9 8 7 9 6 2 [5,] 27 24 21 19 22 31 28 9 18 .......... [111,] 14 14 11 10 14 14 18 13 10 [ reached getOption("max.print") -- omitted 124 rows ] > length(C) [1] 2115 #総観測数2115 > length(C[,1]) [1] 235 #235の観測者 > length(C[1,]) [1] 9 #9年分のデータ |
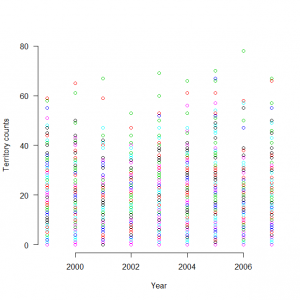
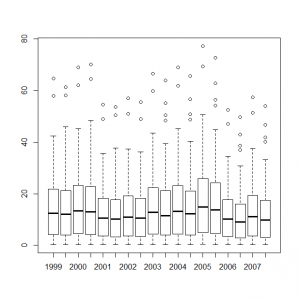
点であらわすとこんなデータ
|
1 |
> matplot(1999:2007, t(C), type = "p",pch=1, lty = 1, lwd = 1, main = "", las = 1, ylab = "Territory counts", xlab = "Year", ylim = c(0, 80), frame = FALSE) |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 |
> table(obs) #観測者 obs 105 109 144 154 169 170 174 189 193 200 221 245 278 297 961 1025 3 9 2 5 1 4 9 7 9 5 1 6 7 7 7 4 1028 1047 1048 1052 1107 1112 1118 1119 1189 1253 1255 1256 1259 1276 1281 1283 9 9 1 9 6 4 1 9 4 2 6 2 9 2 5 1 1332 1341 1356 1364 1373 1379 1383 1385 1386 1397 1414 1419 1439 1452 1455 1458 3 5 2 6 2 1 9 3 1 6 2 9 9 7 25 19 1463 1476 1489 1513 1515 1535 1545 1550 1553 1554 1557 1559 1576 1598 1612 1638 10 1 3 22 19 9 7 9 4 9 8 9 13 3 9 7 1644 1646 1650 1651 1662 1674 1678 1679 1681 1682 1690 1699 1702 1712 1715 1722 9 1 3 10 1 8 9 4 5 8 2 4 3 1 4 1 1724 1728 1730 1742 1745 1750 1756 1758 1760 1771 1792 1795 1805 1809 1820 1828 7 18 9 9 10 9 2 9 2 1 10 1 4 5 9 7 1830 1834 1837 1845 1856 1863 1876 1880 1889 1894 1895 1899 1902 1910 1933 1934 1 42 8 1 16 9 8 9 9 1 9 6 9 5 8 8 1935 1943 1947 1961 1965 1966 1971 1975 1976 1979 1984 1989 1991 1992 1994 2007 3 9 2 15 3 6 3 11 9 9 2 7 4 6 9 9 2010 2011 2018 2029 2031 2037 2040 2043 2048 2049 2050 2055 2058 2060 2064 2066 2 8 14 9 15 5 1 6 9 4 17 3 9 7 5 11 2081 2085 2087 2095 2096 2098 2100 2101 2115 2117 2120 2125 2135 2136 2139 2148 8 8 8 32 1 8 9 9 9 15 2 2 9 8 3 15 2153 2158 2163 2165 2168 2175 2177 2197 2210 2214 2217 2226 2229 2233 2234 2245 10 2 1 1 2 3 9 5 9 9 9 6 9 7 4 7 2246 2254 2261 2266 2270 2335 2337 2343 2345 2347 2353 2375 2380 2381 2387 2394 1 2 2 6 4 6 1 1 5 1 4 5 4 1 5 5 2397 2400 2415 2420 2422 2423 2440 2444 2449 2469 2485 2493 2507 2509 2518 2521 2 5 5 1 1 1 6 5 6 5 4 8 1 1 3 3 2531 2610 2633 2655 2687 3007 3010 3015 3022 3032 3034 3038 3046 3050 3073 3082 1 1 3 2 1 9 9 1 1 9 9 18 5 9 9 9 3091 3092 3094 3136 3161 3176 3196 3202 3213 3256 3257 3258 3259 3260 3261 3263 9 5 9 16 9 7 9 10 9 13 3 3 9 4 5 9 3264 3265 3268 3271 3272 3273 3275 3276 3279 3285 3288 3291 3294 3297 3298 3299 7 16 7 3 7 7 2 3 1 6 5 2 1 11 4 5 3301 3302 3303 3304 3305 3307 3309 3310 3313 3316 3318 3331 3333 3334 3338 11 1 5 5 6 9 4 6 2 3 2 1 1 1 1 > length(table(obs)) #観測者数 [1] 271 > > apply(first, 2, sum, na.rm = TRUE) #年とサイト数は観測者の間でばらついている first1999 first2000 first2001 first2002 first2003 first2004 first2005 first2006 176 37 22 25 40 31 25 33 first2007 24 > #観測者のIDを連続番号に振りなおす > a <- as.numeric(levels(factor(obs))) # All the levels, numeric > newobs <- obs # Gets ObsID from 1:271 > for (j in 1:length(a)){newobs[which(obs==a[j])] <- j } > table(newobs) newobs 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 3 9 2 5 1 4 9 7 9 5 1 6 7 7 7 4 9 9 1 9 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 6 4 1 9 4 2 6 2 9 2 5 1 3 5 2 6 2 1 9 3 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 1 6 2 9 9 7 25 19 10 1 3 22 19 9 7 9 4 9 8 9 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 13 3 9 7 9 1 3 10 1 8 9 4 5 8 2 4 3 1 4 1 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 7 18 9 9 10 9 2 9 2 1 10 1 4 5 9 7 1 42 8 1 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 16 9 8 9 9 1 9 6 9 5 8 8 3 9 2 15 3 6 3 11 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 9 9 2 7 4 6 9 9 2 8 14 9 15 5 1 6 9 4 17 3 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 9 7 5 11 8 8 8 32 1 8 9 9 9 15 2 2 9 8 3 15 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 10 2 1 1 2 3 9 5 9 9 9 6 9 7 4 7 1 2 2 6 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 4 6 1 1 5 1 4 5 4 1 5 5 2 5 5 1 1 1 6 5 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 6 5 4 8 1 1 3 3 1 1 3 2 1 9 9 1 1 9 9 18 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 5 9 9 9 9 5 9 16 9 7 9 10 9 13 3 3 9 4 5 9 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 7 16 7 3 7 7 2 3 1 6 5 2 1 11 4 5 11 1 5 5 261 262 263 264 265 266 267 268 269 270 271 6 9 4 6 2 3 2 1 1 1 1 > #欠損値に数値を与える。 > newobs[is.na(newobs)] <- 272 > table(newobs) newobs 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 3 9 2 5 1 4 9 7 9 5 1 6 7 7 7 4 9 9 1 9 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 6 4 1 9 4 2 6 2 9 2 5 1 3 5 2 6 2 1 9 3 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 1 6 2 9 9 7 25 19 10 1 3 22 19 9 7 9 4 9 8 9 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 13 3 9 7 9 1 3 10 1 8 9 4 5 8 2 4 3 1 4 1 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 7 18 9 9 10 9 2 9 2 1 10 1 4 5 9 7 1 42 8 1 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 16 9 8 9 9 1 9 6 9 5 8 8 3 9 2 15 3 6 3 11 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 9 9 2 7 4 6 9 9 2 8 14 9 15 5 1 6 9 4 17 3 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 9 7 5 11 8 8 8 32 1 8 9 9 9 15 2 2 9 8 3 15 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 10 2 1 1 2 3 9 5 9 9 9 6 9 7 4 7 1 2 2 6 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 4 6 1 1 5 1 4 5 4 1 5 5 2 5 5 1 1 1 6 5 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 6 5 4 8 1 1 3 3 1 1 3 2 1 9 9 1 1 9 9 18 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 5 9 9 9 9 5 9 16 9 7 9 10 9 13 3 3 9 4 5 9 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 7 16 7 3 7 7 2 3 1 6 5 2 1 11 4 5 11 1 5 5 261 262 263 264 265 266 267 268 269 270 271 272 6 9 4 6 2 3 2 1 1 1 1 414 > first[is.na(first)] <- 0 > table(first) first 0 1 1702 413 |
以下、切片だけを含む最も単純なモデルから始めて、徐々に複雑にしていく。
まずは、帰無モデル、切片だけのモデル
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 |
> # (a) Null or intercept-only model > # Specify model in BUGS language > sink("GLM0.txt") > cat(" + model { + + # Prior + alpha ~ dnorm(0, 0.01) # log(mean count) + + # Likelihood + for (i in 1:nyear){ + for (j in 1:nsite){ + C[i,j] ~ dpois(lambda[i,j]) + lambda[i,j] <- exp(log.lambda[i,j]) + log.lambda[i,j] <- alpha + } #j + } #i + } + ",fill = TRUE) > sink() > > # Bundle data > win.data <- list(C = t(C), nsite = nrow(C), nyear = ncol(C)) > > # Initial values > inits <- function() list(alpha = runif(1, -10, 10)) > > # Parameters monitored > params <- c("alpha") > > # MCMC settings > ni <- 1200 > nt <- 2 > nb <- 200 > nc <- 3 > > # Call WinBUGS from R (BRT < 1 min) > out0 <- bugs(win.data, inits, params, "GLM0.txt", n.chains = nc, + n.thin = nt, n.iter = ni, n.burnin = nb, debug = TRUE, bugs.directory = bugs.dir, working.directory = getwd()) > > # Summarize posteriors > print(out0, dig = 3) Inference for Bugs model at "GLM0.txt", fit using WinBUGS, 3 chains, each with 1200 iterations (first 200 discarded), n.thin = 2 n.sims = 1500 iterations saved mean sd 2.5% 25% 50% 75% 97.5% Rhat alpha 2.668 0.006 2.656 2.664 2.668 2.672 2.679 1.002 deviance 32853.287 4.713 32850.000 32850.000 32850.000 32860.000 32860.000 1.001 n.eff alpha 1100 deviance 1500 For each parameter, n.eff is a crude measure of effective sample size, and Rhat is the potential scale reduction factor (at convergence, Rhat=1). DIC info (using the rule, pD = Dbar-Dhat) pD = 1.1 and DIC = 32856.1 DIC is an estimate of expected predictive error (lower deviance is better). |
αの平均μ は2.668 ± 0.006
αの分散σ は32853.287 ± 4.713
αの標準偏差sd 0.005517097 ± 0.460629
mean sd 2.5% 25% 50% 75% 97.5% Rhat
2.668 0.006 2.656 2.664 2.668 2.672 2.679 1.002
deviance 32853.287 4.713 32850.000 32850.000 32850.000 32860.000 32860.000 1.001
αの分布を正規分布に当てはめて描くと、
|
1 |
> curve(dnorm(x, 2.668, 0.005517097), 2.63, 2.7) |
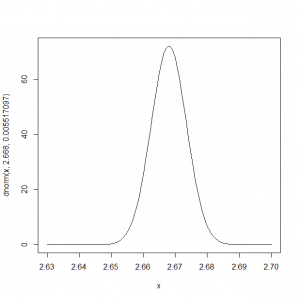
このモデルでは、ヒガラの平均観測密度は、exp(2.67)=14.4
mean 2.5% = 2.656 exp(mean 2.5%) = 14.23922
mean 50% = 2.668 exp(mean 50%) = 14.41112
mean 97.5% = 2.679 exp(mean 97.5%) = 14.57052
> y <- c(mean(C[,1], na.rm=TRUE),mean(C[,2], na.rm=TRUE),mean(C[,3], na.rm=TRUE),mean(C[,4], na.rm=TRUE),mean(C[,5], na.rm=TRUE),mean(C[,6], na.rm=TRUE),mean(C[,6], na.rm=TRUE),mean(C[,8], na.rm=TRUE),mean(C[,9], na.rm=TRUE)) 年ごとの平均値と、今回ベイズ流に求めた全体の平均値±95%信用区間 > matplot(1999:2007, y, type = “l”, lty = 1, lwd = 1, main = “”, las = 1, ylab = “Territory counts”, xlab = “Year”, ylim = c(0, 80), frame = FALSE)
> abline(h=14.41112, col=”red”)
> abline(h=14.23922, col = gray(0.5))
> abline(h=14.57052, col = gray(0.5))
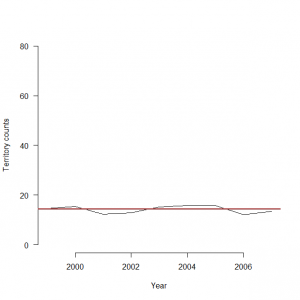
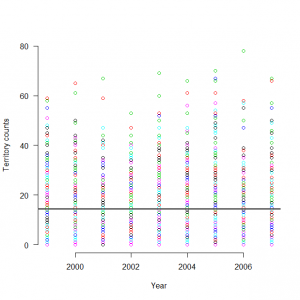
こんなところがこのモデル化による結果というところか。
つまり、全体の平均で置き換えたというところか。
次に固定サイト効果を追加する。サイトsiteは、235個含まれている。
これらのサイトごとにパラメータαi = ポアソン分布の平均値を正規分布として定義する。サイトごとに計測値がどうかという情報が得られるということか。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 |
> # (b) Fixed site effects > # Specify model in BUGS language > sink("GLM1.txt") > cat(" + model { + + # Priors + for (j in 1:nsite){ + alpha[j] ~ dnorm(0, 0.01) # Site effects + } + + # Likelihood + for (i in 1:nyear){ + for (j in 1:nsite){ + C[i,j] ~ dpois(lambda[i,j]) + lambda[i,j] <- exp(log.lambda[i,j]) + log.lambda[i,j] <- alpha[j] + } #j + } #i + } + ",fill = TRUE) > sink() > > # Bundle data > win.data <- list(C = t(C), nsite = nrow(C), nyear = ncol(C)) > > # Initial values (not required for all) > inits <- function() list(alpha = runif(235, -1, 1)) > > # Parameters monitored > params <- c("alpha") > > # MCMC settings > ni <- 1200 > nt <- 2 > nb <- 200 > nc <- 3 > > # Call WinBUGS from R (BRT < 1 min) > out1 <- bugs(win.data, inits, params, "GLM1.txt", n.chains = nc, + n.thin = nt, n.iter = ni, n.burnin = nb, debug = TRUE, bugs.directory = bugs.dir, working.directory = getwd()) > > # Summarize posteriors > print(out1, dig = 2) Inference for Bugs model at "GLM1.txt", fit using WinBUGS, 3 chains, each with 1200 iterations (first 200 discarded), n.thin = 2 n.sims = 1500 iterations saved mean sd 2.5% 25% 50% 75% 97.5% Rhat alpha[1] -0.20 0.36 -0.97 -0.42 -0.18 0.05 0.44 1.00 alpha[2] -0.50 0.42 -1.39 -0.76 -0.49 -0.21 0.24 1.00 alpha[3] 2.46 0.10 2.25 2.39 2.46 2.53 2.65 1.00 alpha[4] 1.98 0.12 1.71 1.90 1.98 2.07 2.21 1.00 alpha[5] 3.09 0.07 2.94 3.05 3.09 3.14 3.23 1.00 alpha[6] -1.19 0.64 -2.64 -1.57 -1.13 -0.75 -0.10 1.00 alpha[7] 0.78 0.25 0.26 0.62 0.79 0.96 1.23 1.00 alpha[8] 2.71 0.09 2.54 2.65 2.71 2.77 2.87 1.00 alpha[9] 0.17 0.32 -0.50 -0.02 0.18 0.40 0.74 1.00 alpha[10] 1.75 0.14 1.46 1.66 1.75 1.84 2.02 1.00 alpha[11] 3.36 0.06 3.23 3.32 3.36 3.40 3.47 1.00 alpha[12] 3.56 0.06 3.45 3.52 3.56 3.59 3.66 1.00 alpha[13] 2.75 0.08 2.60 2.69 2.75 2.80 2.90 1.00 alpha[14] 1.76 0.15 1.46 1.66 1.75 1.86 2.03 1.00 alpha[15] 1.54 0.17 1.19 1.43 1.54 1.65 1.86 1.00 alpha[16] 2.51 0.10 2.32 2.45 2.52 2.58 2.70 1.00 alpha[17] 2.41 0.10 2.23 2.35 2.41 2.48 2.60 1.00 alpha[18] 2.71 0.09 2.54 2.66 2.72 2.77 2.88 1.00 alpha[19] 3.58 0.06 3.46 3.54 3.58 3.61 3.69 1.00 alpha[20] 2.62 0.09 2.44 2.56 2.62 2.68 2.79 1.00 alpha[21] 2.34 0.10 2.12 2.27 2.34 2.41 2.54 1.00 alpha[22] 1.96 0.13 1.69 1.88 1.96 2.05 2.19 1.00 alpha[23] 2.53 0.09 2.35 2.47 2.54 2.60 2.71 1.00 alpha[24] -0.95 0.51 -2.08 -1.28 -0.91 -0.58 -0.08 1.00 alpha[25] 2.77 0.08 2.60 2.71 2.77 2.82 2.92 1.00 alpha[26] 2.18 0.11 1.96 2.11 2.18 2.25 2.41 1.00 alpha[27] 2.95 0.08 2.80 2.90 2.96 3.00 3.10 1.00 alpha[28] 3.64 0.05 3.54 3.61 3.64 3.68 3.74 1.00 alpha[29] 1.55 0.15 1.24 1.45 1.55 1.66 1.84 1.00 alpha[30] 0.18 0.30 -0.44 -0.02 0.20 0.39 0.71 1.00 alpha[31] 1.55 0.16 1.25 1.45 1.56 1.67 1.84 1.00 alpha[32] 3.27 0.06 3.15 3.23 3.27 3.32 3.41 1.00 alpha[33] 4.18 0.04 4.10 4.15 4.18 4.21 4.26 1.00 alpha[34] -0.09 0.40 -0.94 -0.33 -0.07 0.18 0.60 1.00 alpha[35] 3.60 0.05 3.50 3.56 3.60 3.64 3.70 1.00 alpha[36] 2.68 0.10 2.48 2.61 2.68 2.74 2.87 1.00 alpha[37] 3.47 0.06 3.35 3.43 3.47 3.50 3.58 1.00 alpha[38] -0.82 0.53 -1.95 -1.15 -0.79 -0.45 0.11 1.00 alpha[39] 2.57 0.09 2.39 2.51 2.57 2.63 2.74 1.00 alpha[40] 3.09 0.07 2.94 3.04 3.09 3.13 3.22 1.00 alpha[41] 1.97 0.13 1.71 1.89 1.98 2.06 2.21 1.00 alpha[42] 1.91 0.14 1.62 1.82 1.91 2.00 2.17 1.00 alpha[43] 3.00 0.07 2.85 2.95 3.00 3.05 3.14 1.00 alpha[44] 4.07 0.04 3.99 4.04 4.07 4.10 4.16 1.00 alpha[45] 3.38 0.06 3.26 3.34 3.38 3.42 3.51 1.00 alpha[46] 1.46 0.16 1.15 1.35 1.46 1.57 1.76 1.00 alpha[47] -1.78 0.79 -3.60 -2.22 -1.68 -1.24 -0.54 1.00 alpha[48] 3.26 0.06 3.14 3.22 3.26 3.31 3.39 1.00 alpha[49] 3.16 0.07 3.02 3.12 3.16 3.21 3.30 1.00 alpha[50] 3.00 0.07 2.86 2.96 3.00 3.06 3.15 1.00 alpha[51] 0.71 0.23 0.26 0.57 0.72 0.87 1.15 1.00 alpha[52] 2.82 0.08 2.66 2.77 2.82 2.88 2.97 1.00 alpha[53] 2.66 0.09 2.49 2.60 2.66 2.72 2.82 1.01 alpha[54] 2.46 0.10 2.26 2.40 2.47 2.53 2.64 1.00 alpha[55] 2.92 0.08 2.76 2.87 2.92 2.97 3.07 1.00 alpha[56] 0.66 0.25 0.16 0.50 0.65 0.84 1.13 1.00 alpha[57] 3.70 0.05 3.59 3.67 3.71 3.74 3.81 1.00 alpha[58] 3.12 0.07 2.98 3.07 3.12 3.16 3.25 1.00 alpha[59] 3.10 0.07 2.96 3.06 3.10 3.15 3.24 1.00 alpha[60] 1.11 0.20 0.69 0.98 1.12 1.25 1.50 1.00 alpha[61] 2.82 0.08 2.66 2.76 2.82 2.87 2.97 1.00 alpha[62] 2.25 0.11 2.02 2.18 2.25 2.33 2.46 1.00 alpha[63] 3.02 0.07 2.88 2.97 3.02 3.07 3.16 1.00 alpha[64] 3.16 0.07 3.02 3.11 3.16 3.21 3.30 1.00 alpha[65] 3.46 0.06 3.34 3.42 3.46 3.50 3.57 1.00 alpha[66] 0.14 0.30 -0.51 -0.06 0.16 0.35 0.67 1.00 alpha[67] 3.52 0.06 3.41 3.48 3.52 3.56 3.62 1.00 alpha[68] 0.66 0.25 0.11 0.49 0.66 0.84 1.12 1.00 alpha[69] 2.65 0.09 2.48 2.59 2.65 2.71 2.82 1.00 alpha[70] 0.48 0.25 -0.04 0.31 0.49 0.66 0.94 1.00 alpha[71] -0.17 0.38 -0.96 -0.41 -0.16 0.10 0.50 1.00 alpha[72] 3.53 0.06 3.42 3.49 3.53 3.56 3.64 1.00 alpha[73] 2.68 0.09 2.51 2.62 2.68 2.74 2.85 1.00 alpha[74] 2.81 0.08 2.65 2.76 2.81 2.86 2.96 1.00 alpha[75] 0.40 0.27 -0.15 0.22 0.42 0.60 0.91 1.00 alpha[76] 1.19 0.18 0.81 1.08 1.20 1.31 1.51 1.00 alpha[77] 2.72 0.08 2.56 2.66 2.72 2.77 2.88 1.00 alpha[78] -1.76 0.81 -3.61 -2.22 -1.66 -1.22 -0.41 1.00 alpha[79] 3.32 0.07 3.19 3.28 3.32 3.37 3.45 1.00 alpha[80] 2.09 0.12 1.86 2.01 2.09 2.17 2.31 1.00 alpha[81] 2.82 0.09 2.64 2.76 2.82 2.88 3.00 1.00 alpha[82] 1.90 0.13 1.64 1.82 1.90 1.99 2.15 1.00 alpha[83] 2.30 0.10 2.10 2.23 2.31 2.37 2.50 1.00 alpha[84] 3.36 0.06 3.24 3.32 3.36 3.40 3.48 1.00 alpha[85] 2.64 0.09 2.47 2.58 2.64 2.70 2.81 1.00 alpha[86] 3.08 0.07 2.94 3.04 3.08 3.13 3.22 1.00 alpha[87] 3.49 0.06 3.36 3.45 3.49 3.52 3.60 1.00 alpha[88] 3.22 0.07 3.08 3.18 3.23 3.27 3.36 1.00 alpha[89] 3.16 0.07 3.02 3.11 3.16 3.21 3.30 1.00 alpha[90] 2.64 0.09 2.47 2.58 2.65 2.70 2.80 1.00 alpha[91] 1.62 0.15 1.32 1.52 1.63 1.72 1.91 1.00 alpha[92] 2.72 0.09 2.55 2.66 2.72 2.78 2.88 1.00 alpha[93] 2.54 0.09 2.36 2.48 2.55 2.61 2.73 1.01 alpha[94] 2.39 0.10 2.19 2.33 2.39 2.46 2.58 1.00 alpha[95] 1.56 0.15 1.23 1.46 1.56 1.66 1.84 1.00 alpha[96] 3.59 0.06 3.48 3.55 3.58 3.62 3.69 1.00 alpha[97] 2.79 0.09 2.62 2.73 2.79 2.85 2.95 1.00 alpha[98] 2.17 0.11 1.95 2.10 2.17 2.25 2.39 1.00 alpha[99] 3.66 0.05 3.55 3.62 3.66 3.70 3.76 1.00 alpha[100] 3.08 0.07 2.94 3.04 3.08 3.13 3.22 1.00 alpha[101] 2.46 0.10 2.27 2.39 2.46 2.53 2.65 1.00 alpha[102] 3.13 0.07 2.99 3.08 3.13 3.18 3.27 1.00 alpha[103] -1.75 0.80 -3.56 -2.21 -1.66 -1.18 -0.50 1.00 alpha[104] 3.42 0.06 3.30 3.38 3.42 3.46 3.54 1.00 alpha[105] 2.92 0.08 2.74 2.86 2.92 2.97 3.08 1.00 alpha[106] 2.14 0.11 1.91 2.06 2.14 2.21 2.34 1.00 alpha[107] -0.57 0.47 -1.59 -0.85 -0.52 -0.25 0.24 1.00 alpha[108] -1.75 0.80 -3.58 -2.18 -1.64 -1.22 -0.52 1.00 alpha[109] 1.69 0.14 1.41 1.59 1.69 1.78 1.96 1.00 alpha[110] 3.37 0.06 3.24 3.33 3.37 3.41 3.48 1.00 alpha[111] 2.57 0.09 2.39 2.51 2.58 2.64 2.75 1.00 n.eff alpha[1] 1500 alpha[2] 1500 alpha[3] 460 alpha[4] 1500 alpha[5] 1500 alpha[6] 1000 alpha[7] 1500 alpha[8] 1500 alpha[9] 1500 alpha[10] 1500 alpha[11] 1500 alpha[12] 1000 alpha[13] 1500 alpha[14] 1500 alpha[15] 1200 alpha[16] 1500 alpha[17] 860 alpha[18] 1400 alpha[19] 700 alpha[20] 1200 alpha[21] 1500 alpha[22] 1200 alpha[23] 1500 alpha[24] 1500 alpha[25] 1500 alpha[26] 1500 alpha[27] 1500 alpha[28] 1500 alpha[29] 1500 alpha[30] 1400 alpha[31] 1500 alpha[32] 1500 alpha[33] 570 alpha[34] 1500 alpha[35] 1000 alpha[36] 700 alpha[37] 1500 alpha[38] 1200 alpha[39] 1300 alpha[40] 1500 alpha[41] 1500 alpha[42] 1500 alpha[43] 510 alpha[44] 1500 alpha[45] 1200 alpha[46] 730 alpha[47] 1500 alpha[48] 1500 alpha[49] 1400 alpha[50] 1500 alpha[51] 1500 alpha[52] 920 alpha[53] 860 alpha[54] 1500 alpha[55] 1500 alpha[56] 1500 alpha[57] 1500 alpha[58] 1500 alpha[59] 1500 alpha[60] 1500 alpha[61] 1100 alpha[62] 1500 alpha[63] 620 alpha[64] 1400 alpha[65] 1500 alpha[66] 1500 alpha[67] 1500 alpha[68] 1500 alpha[69] 480 alpha[70] 1500 alpha[71] 860 alpha[72] 1500 alpha[73] 1500 alpha[74] 990 alpha[75] 960 alpha[76] 700 alpha[77] 1500 alpha[78] 1500 alpha[79] 1500 alpha[80] 1500 alpha[81] 1500 alpha[82] 1500 alpha[83] 1500 alpha[84] 1500 alpha[85] 1500 alpha[86] 970 alpha[87] 1500 alpha[88] 1500 alpha[89] 580 alpha[90] 1500 alpha[91] 610 alpha[92] 1500 alpha[93] 220 alpha[94] 1500 alpha[95] 1500 alpha[96] 1500 alpha[97] 530 alpha[98] 1500 alpha[99] 1500 alpha[100] 1500 alpha[101] 1500 alpha[102] 1500 alpha[103] 1500 alpha[104] 1500 alpha[105] 720 alpha[106] 1500 alpha[107] 1500 alpha[108] 990 alpha[109] 1400 alpha[110] 1500 alpha[111] 1500 [ reached getOption("max.print") -- omitted 125 rows ] For each parameter, n.eff is a crude measure of effective sample size, and Rhat is the potential scale reduction factor (at convergence, Rhat=1). DIC info (using the rule, pD = Dbar-Dhat) pD = 232.5 and DIC = 11920.5 DIC is an estimate of expected predictive error (lower deviance is better). > |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 |
> length(out1$mean$alpha) [1] 235 > out1$mean$alpha [1] -0.19527917 -0.48912494 2.45791133 1.97780133 3.09235333 -1.15894377 [7] 0.78798295 2.70868200 0.17196934 1.74406667 3.36595733 3.55249133 [13] 2.74636400 1.75312800 1.54987767 2.51234467 2.40703867 2.71388667 [19] 3.57859933 2.62405533 2.33972800 1.95742933 2.53615067 -0.95608938 [25] 2.76783933 2.17910133 2.95065333 3.64236467 1.55554467 0.16423942 [31] 1.55465733 3.27887200 4.18009733 -0.05902481 3.59994067 2.67844733 [37] 3.46848533 -0.83284968 2.57371267 3.08844733 1.97271467 1.91435000 [43] 3.00528000 4.07026733 3.37754200 1.45107320 -1.78909766 3.26025267 [49] 3.16248867 3.00359533 0.72428351 2.82479133 2.65983600 2.46499533 [55] 2.91823000 0.66928351 3.70413067 3.11509333 3.09999733 1.11932487 [61] 2.81700667 2.24907867 3.02236267 3.16256200 3.45480667 0.14867858 [67] 3.51214933 0.65484273 2.64852333 0.47075776 -0.18812376 3.52427400 [73] 2.68009733 2.81459000 0.41088601 1.18891460 2.71471600 -1.76380229 [79] 3.31663400 2.08592800 2.82393133 1.90357800 2.30995200 3.36367400 [85] 2.64317533 3.08230867 3.48455200 3.22587533 3.16227133 2.64747667 [91] 1.61695067 2.71745000 2.54342333 2.39598333 1.55054200 3.59021467 [97] 2.79181600 2.18191600 3.65971000 3.08732000 2.46452467 3.12824267 [103] -1.80363373 3.41854200 2.91444600 2.14606467 -0.58298858 -1.77668209 [109] 1.68543200 3.36283667 2.57163933 3.49446200 2.77768933 2.17957400 [115] 1.92206400 3.14208667 0.72262968 2.14152800 2.42681667 2.68260200 [121] 2.97478667 2.08560133 0.05622645 -0.48612395 -1.73437083 2.86563333 [127] 2.55873267 -0.69022847 1.85452800 2.20556533 2.44742000 -0.03820907 [133] 2.41235000 1.25114580 -0.94412843 2.64992800 3.68459267 2.54775200 [139] 1.68669933 2.48121533 2.96464200 3.13013200 -0.34551059 -1.29797401 [145] 2.53471800 3.18640067 2.28510467 2.13905867 3.34846667 1.39857153 [151] 3.39205200 3.42567000 2.01387267 1.54476007 1.94181867 2.03038267 [157] -0.70217280 0.99629993 2.95277800 -1.13985623 2.56659333 0.91929687 [163] 2.55181000 3.25291800 2.86836133 0.82402970 -0.92691642 0.24594579 [169] 1.28742787 3.05688400 2.00045467 3.02263800 3.24132867 0.40664842 [175] 2.50465267 1.54863367 -1.27109263 -0.56773603 2.56470200 -0.05447273 [181] 2.06804533 2.89965933 0.52431989 1.40314947 2.08260933 2.13887333 [187] 3.41683600 3.23821533 3.33542600 2.15372933 3.29236667 2.68752133 [193] 3.40467733 1.98144933 2.19265867 2.67951000 0.47078238 3.61845000 [199] -2.65552493 3.23069467 2.81164067 0.15854382 2.80168933 1.74997667 [205] -0.69290116 2.02956733 3.24836667 2.58358400 2.95483800 2.04001667 [211] 3.53811467 2.53307667 3.05228467 0.15870975 2.52036333 3.09389800 [217] 2.92771400 3.24369000 2.65656800 3.14299333 1.11815767 -2.73284019 [223] 2.56156800 0.87175740 3.55017600 1.37653413 0.41103329 -0.68500978 [229] 2.80794800 3.33762267 3.76101467 3.66903467 3.67718067 3.36329200 [235] 3.58923667 |
|
1 |
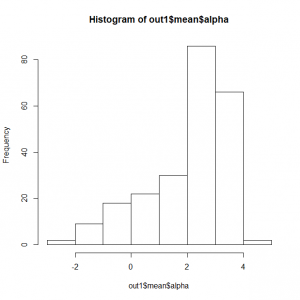
> hist((out1$mean$alpha) |
|
1 2 3 4 5 |
> mean(out1$mean$alpha) [1] 2.030321 > mean(exp(out1$mean$alpha)) [1] 14.25242 > hist(exp(out1$mean$alpha)) |
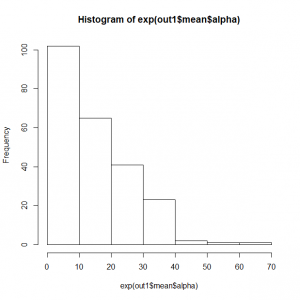
これだけの調査レポートだと、分析やり直しとなるであろう。
年ごとはどうなっているのかに答える必要があるだろう。
次は、固定サイト効果に固定年効果を組み込む
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281 282 283 284 |
> # (c) Fixed site and fixed year effects > # Specify model in BUGS language > sink("GLM2.txt") > cat(" + model { + + # Priors + for (j in 1:nsite){ # site effects + alpha[j] ~ dnorm(0, 0.01) + } + + for (i in 2:nyear){ # nyear-1 year effects + eps[i] ~ dnorm(0, 0.01) + } + eps[1] <- 0 # Aliased + + # Likelihood + for (i in 1:nyear){ + for (j in 1:nsite){ + C[i,j] ~ dpois(lambda[i,j]) + lambda[i,j] <- exp(log.lambda[i,j]) + log.lambda[i,j] <- alpha[j] + eps[i] + } #j + } #i + } + ",fill = TRUE) > sink() > > # Bundle data > win.data <- list(C = t(C), nsite = nrow(C), nyear = ncol(C)) > > # Initial values > inits <- function() list(alpha = runif(235, -1, 1), eps = c(NA, runif(8, -1, 1))) > > # Parameters monitored > params <- c("alpha", "eps") > > # MCMC settings > ni <- 1200 > nt <- 2 > nb <- 200 > nc <- 3 > > # Call WinBUGS from R (BRT < 1 min) > out2 <- bugs(win.data, inits, params, "GLM2.txt", n.chains = nc, + n.thin = nt, n.iter = ni, n.burnin = nb, debug = TRUE, bugs.directory = bugs.dir, working.directory = getwd()) > > # Summarize posteriors > print(out2, dig = 2) Inference for Bugs model at "GLM2.txt", fit using WinBUGS, 3 chains, each with 1200 iterations (first 200 discarded), n.thin = 2 n.sims = 1500 iterations saved mean sd 2.5% 25% 50% 75% 97.5% Rhat alpha[1] -0.17 0.36 -0.92 -0.39 -0.15 0.08 0.49 1.00 alpha[2] -0.52 0.43 -1.43 -0.80 -0.48 -0.22 0.24 1.00 alpha[3] 2.46 0.10 2.26 2.38 2.46 2.53 2.66 1.00 alpha[4] 1.98 0.12 1.73 1.90 1.98 2.06 2.22 1.00 alpha[5] 3.09 0.07 2.94 3.04 3.09 3.14 3.22 1.00 alpha[6] -1.18 0.65 -2.61 -1.54 -1.10 -0.74 -0.11 1.00 alpha[7] 0.75 0.25 0.23 0.59 0.77 0.92 1.22 1.00 alpha[8] 2.71 0.09 2.54 2.65 2.71 2.77 2.88 1.00 alpha[9] 0.19 0.34 -0.52 -0.03 0.21 0.42 0.77 1.00 alpha[10] 1.74 0.14 1.46 1.65 1.74 1.83 2.01 1.00 alpha[11] 3.36 0.06 3.24 3.32 3.36 3.40 3.49 1.00 alpha[12] 3.55 0.06 3.44 3.51 3.55 3.59 3.66 1.00 alpha[13] 2.75 0.09 2.58 2.69 2.75 2.81 2.91 1.00 alpha[14] 1.74 0.15 1.44 1.64 1.74 1.84 2.01 1.00 alpha[15] 1.55 0.16 1.23 1.44 1.56 1.66 1.85 1.00 alpha[16] 2.51 0.10 2.31 2.45 2.52 2.58 2.70 1.00 alpha[17] 2.41 0.10 2.22 2.35 2.41 2.48 2.59 1.00 alpha[18] 2.71 0.09 2.53 2.65 2.71 2.77 2.88 1.00 alpha[19] 3.58 0.06 3.46 3.54 3.58 3.62 3.70 1.01 alpha[20] 2.62 0.09 2.44 2.56 2.62 2.68 2.80 1.00 alpha[21] 2.34 0.11 2.12 2.27 2.34 2.41 2.55 1.00 alpha[22] 1.96 0.13 1.67 1.87 1.97 2.06 2.21 1.00 alpha[23] 2.53 0.09 2.34 2.47 2.53 2.59 2.71 1.00 alpha[24] -0.94 0.53 -2.04 -1.26 -0.91 -0.57 -0.03 1.00 alpha[25] 2.77 0.08 2.60 2.71 2.77 2.82 2.92 1.00 alpha[26] 2.18 0.12 1.94 2.10 2.18 2.26 2.40 1.00 alpha[27] 2.95 0.08 2.80 2.90 2.95 3.00 3.11 1.01 alpha[28] 3.64 0.05 3.54 3.60 3.64 3.68 3.75 1.00 alpha[29] 1.55 0.16 1.24 1.44 1.55 1.66 1.85 1.00 alpha[30] 0.15 0.31 -0.52 -0.07 0.16 0.38 0.69 1.00 alpha[31] 1.55 0.15 1.23 1.45 1.55 1.65 1.83 1.00 alpha[32] 3.28 0.07 3.14 3.23 3.27 3.32 3.40 1.00 alpha[33] 4.18 0.04 4.09 4.15 4.18 4.21 4.26 1.00 alpha[34] -0.13 0.39 -0.98 -0.37 -0.11 0.15 0.55 1.00 alpha[35] 3.60 0.06 3.48 3.56 3.60 3.64 3.71 1.00 alpha[36] 2.66 0.10 2.45 2.59 2.66 2.73 2.85 1.00 alpha[37] 3.46 0.06 3.34 3.42 3.46 3.51 3.59 1.00 alpha[38] -0.82 0.55 -1.99 -1.15 -0.79 -0.44 0.11 1.00 alpha[39] 2.57 0.09 2.38 2.50 2.57 2.63 2.74 1.00 alpha[40] 3.09 0.07 2.93 3.04 3.09 3.13 3.22 1.00 alpha[41] 1.97 0.13 1.70 1.88 1.97 2.06 2.21 1.00 alpha[42] 1.90 0.14 1.63 1.80 1.89 1.98 2.16 1.00 alpha[43] 3.00 0.08 2.85 2.95 3.00 3.06 3.14 1.00 alpha[44] 4.07 0.05 3.97 4.04 4.07 4.10 4.16 1.00 alpha[45] 3.37 0.06 3.25 3.33 3.38 3.42 3.50 1.00 alpha[46] 1.46 0.16 1.13 1.35 1.46 1.58 1.74 1.00 alpha[47] -1.77 0.81 -3.61 -2.24 -1.68 -1.19 -0.47 1.00 alpha[48] 3.26 0.07 3.13 3.21 3.26 3.30 3.39 1.00 alpha[49] 3.16 0.07 3.02 3.12 3.16 3.21 3.29 1.00 alpha[50] 3.00 0.08 2.85 2.96 3.01 3.06 3.15 1.00 alpha[51] 0.72 0.23 0.24 0.58 0.73 0.88 1.16 1.00 alpha[52] 2.82 0.08 2.66 2.77 2.82 2.88 2.97 1.00 alpha[53] 2.65 0.09 2.48 2.59 2.65 2.71 2.82 1.00 alpha[54] 2.46 0.10 2.25 2.39 2.46 2.53 2.66 1.00 alpha[55] 2.92 0.08 2.76 2.87 2.92 2.97 3.08 1.00 alpha[56] 0.69 0.25 0.18 0.52 0.70 0.86 1.13 1.00 alpha[57] 3.70 0.06 3.59 3.67 3.70 3.74 3.81 1.00 alpha[58] 3.11 0.07 2.97 3.07 3.11 3.16 3.25 1.00 alpha[59] 3.10 0.07 2.96 3.05 3.10 3.15 3.24 1.00 alpha[60] 1.11 0.20 0.73 0.98 1.12 1.26 1.50 1.01 alpha[61] 2.81 0.08 2.65 2.76 2.82 2.87 2.97 1.00 alpha[62] 2.25 0.11 2.02 2.17 2.25 2.32 2.46 1.00 alpha[63] 3.02 0.07 2.88 2.97 3.02 3.07 3.16 1.00 alpha[64] 3.16 0.07 3.02 3.11 3.16 3.21 3.30 1.00 alpha[65] 3.46 0.06 3.34 3.42 3.46 3.50 3.57 1.00 alpha[66] 0.15 0.31 -0.49 -0.04 0.16 0.36 0.74 1.00 alpha[67] 3.51 0.06 3.39 3.47 3.52 3.56 3.63 1.00 alpha[68] 0.66 0.25 0.12 0.50 0.66 0.82 1.13 1.00 alpha[69] 2.65 0.09 2.47 2.59 2.66 2.71 2.83 1.00 alpha[70] 0.47 0.26 -0.08 0.30 0.49 0.65 0.95 1.00 alpha[71] -0.19 0.36 -0.95 -0.43 -0.17 0.06 0.45 1.00 alpha[72] 3.52 0.06 3.41 3.48 3.52 3.56 3.64 1.00 alpha[73] 2.68 0.09 2.51 2.62 2.68 2.74 2.84 1.00 alpha[74] 2.81 0.08 2.65 2.75 2.81 2.87 2.98 1.01 alpha[75] 0.40 0.27 -0.20 0.22 0.42 0.59 0.89 1.00 alpha[76] 1.19 0.19 0.82 1.06 1.19 1.32 1.53 1.00 alpha[77] 2.72 0.09 2.54 2.66 2.72 2.78 2.88 1.00 alpha[78] -1.77 0.80 -3.58 -2.23 -1.66 -1.21 -0.49 1.00 alpha[79] 3.33 0.07 3.18 3.28 3.32 3.37 3.46 1.00 alpha[80] 2.08 0.12 1.84 2.00 2.08 2.16 2.31 1.00 alpha[81] 2.78 0.10 2.60 2.72 2.79 2.85 2.97 1.00 alpha[82] 1.90 0.13 1.64 1.81 1.90 1.99 2.14 1.00 alpha[83] 2.31 0.11 2.09 2.23 2.31 2.38 2.52 1.00 alpha[84] 3.36 0.06 3.23 3.32 3.36 3.40 3.48 1.00 alpha[85] 2.64 0.09 2.46 2.58 2.64 2.70 2.81 1.00 alpha[86] 3.08 0.08 2.93 3.03 3.08 3.13 3.22 1.00 alpha[87] 3.48 0.06 3.37 3.44 3.48 3.53 3.59 1.00 alpha[88] 3.22 0.07 3.08 3.18 3.22 3.27 3.35 1.00 alpha[89] 3.16 0.07 3.02 3.12 3.16 3.21 3.30 1.00 alpha[90] 2.64 0.09 2.46 2.58 2.64 2.70 2.81 1.00 alpha[91] 1.62 0.15 1.32 1.52 1.62 1.73 1.90 1.00 alpha[92] 2.71 0.09 2.54 2.66 2.71 2.77 2.89 1.00 alpha[93] 2.54 0.09 2.34 2.48 2.55 2.61 2.72 1.00 alpha[94] 2.39 0.10 2.19 2.33 2.39 2.46 2.59 1.00 alpha[95] 1.55 0.15 1.23 1.45 1.56 1.66 1.83 1.00 alpha[96] 3.59 0.05 3.48 3.55 3.59 3.62 3.69 1.00 alpha[97] 2.79 0.09 2.61 2.73 2.79 2.85 2.97 1.00 alpha[98] 2.18 0.11 1.95 2.10 2.18 2.26 2.40 1.00 alpha[99] 3.66 0.06 3.55 3.62 3.66 3.70 3.77 1.01 alpha[100] 3.08 0.07 2.94 3.04 3.08 3.13 3.22 1.00 alpha[101] 2.46 0.10 2.26 2.40 2.46 2.53 2.65 1.00 alpha[102] 3.13 0.07 2.98 3.08 3.13 3.18 3.26 1.00 alpha[103] -1.75 0.79 -3.60 -2.20 -1.67 -1.18 -0.48 1.00 alpha[104] 3.41 0.06 3.29 3.37 3.42 3.46 3.53 1.00 alpha[105] 2.91 0.08 2.74 2.86 2.91 2.97 3.07 1.00 alpha[106] 2.14 0.11 1.91 2.07 2.15 2.22 2.36 1.00 alpha[107] -0.58 0.47 -1.59 -0.89 -0.55 -0.24 0.25 1.00 alpha[108] -1.78 0.80 -3.75 -2.25 -1.69 -1.20 -0.52 1.00 alpha[109] 1.68 0.14 1.39 1.59 1.69 1.78 1.95 1.00 alpha[110] 3.36 0.07 3.23 3.32 3.36 3.41 3.49 1.00 alpha[111] 2.56 0.09 2.38 2.51 2.57 2.63 2.75 1.00 n.eff alpha[1] 1300 alpha[2] 1500 alpha[3] 1500 alpha[4] 1500 alpha[5] 1500 alpha[6] 1200 alpha[7] 1500 alpha[8] 1500 alpha[9] 1500 alpha[10] 1500 alpha[11] 1500 alpha[12] 1500 alpha[13] 720 alpha[14] 1500 alpha[15] 1500 alpha[16] 1500 alpha[17] 1500 alpha[18] 1500 alpha[19] 380 alpha[20] 1500 alpha[21] 910 alpha[22] 510 alpha[23] 1500 alpha[24] 1500 alpha[25] 1500 alpha[26] 1500 alpha[27] 360 alpha[28] 1400 alpha[29] 1500 alpha[30] 1500 alpha[31] 680 alpha[32] 1500 alpha[33] 1500 alpha[34] 1500 alpha[35] 1500 alpha[36] 1500 alpha[37] 1500 alpha[38] 1500 alpha[39] 1500 alpha[40] 1500 alpha[41] 1500 alpha[42] 1500 alpha[43] 1500 alpha[44] 660 alpha[45] 540 alpha[46] 1500 alpha[47] 1400 alpha[48] 1100 alpha[49] 1500 alpha[50] 1500 alpha[51] 1500 alpha[52] 1500 alpha[53] 1500 alpha[54] 1500 alpha[55] 1500 alpha[56] 1000 alpha[57] 1500 alpha[58] 1500 alpha[59] 720 alpha[60] 1500 alpha[61] 1500 alpha[62] 1500 alpha[63] 1500 alpha[64] 540 alpha[65] 1400 alpha[66] 1500 alpha[67] 1500 alpha[68] 1500 alpha[69] 420 alpha[70] 1500 alpha[71] 860 alpha[72] 1500 alpha[73] 1500 alpha[74] 240 alpha[75] 1500 alpha[76] 1500 alpha[77] 1500 alpha[78] 1500 alpha[79] 1300 alpha[80] 690 alpha[81] 800 alpha[82] 1300 alpha[83] 1500 alpha[84] 880 alpha[85] 1500 alpha[86] 1500 alpha[87] 1500 alpha[88] 480 alpha[89] 1500 alpha[90] 1500 alpha[91] 650 alpha[92] 1500 alpha[93] 960 alpha[94] 1500 alpha[95] 800 alpha[96] 1500 alpha[97] 480 alpha[98] 1500 alpha[99] 390 alpha[100] 1500 alpha[101] 1500 alpha[102] 1500 alpha[103] 1000 alpha[104] 1500 alpha[105] 1500 alpha[106] 1500 alpha[107] 1500 alpha[108] 1300 alpha[109] 1300 alpha[110] 1500 alpha[111] 1500 [ reached getOption("max.print") -- omitted 133 rows ] For each parameter, n.eff is a crude measure of effective sample size, and Rhat is the potential scale reduction factor (at convergence, Rhat=1). DIC info (using the rule, pD = Dbar-Dhat) pD = 241.4 and DIC = 11478.7 DIC is an estimate of expected predictive error (lower deviance is better). |
|
1 2 3 4 5 |
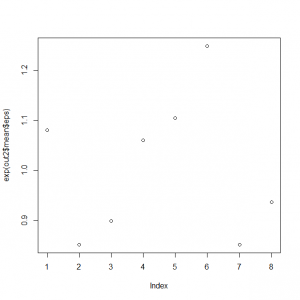
> exp(out2$mean$eps) [1] 1.0801500 0.8518834 0.8990630 1.0599091 1.1047034 1.2489761 0.8515608 [8] 0.9370838 > mean(exp(out2$mean$eps)) [1] 1.004166 |
年によって、計測数1程度影響することがわかる。
|
1 |
> plot(exp(out2$mean$eps)) |
|
1 |
> plot(mean(exp(out2$mean$alpha)) + exp(out2$mean$eps), xlab = "Year", ylim = c(0, 80)) |
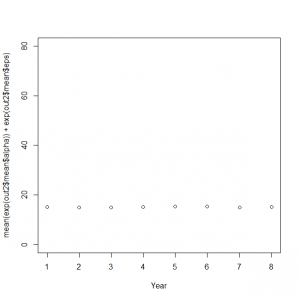
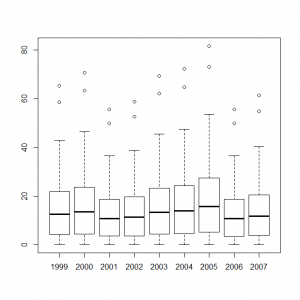
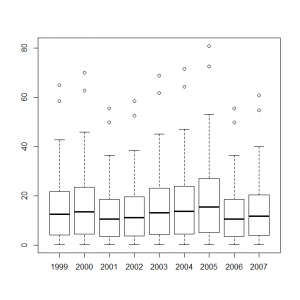
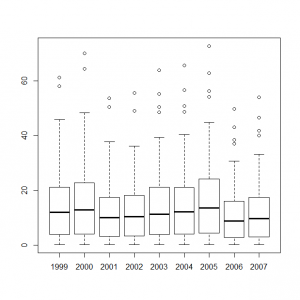
サイト効果に年ごとの固定効果を組み込んだモデルをボックスプロット表示してみる。
|
1 2 3 4 5 6 7 8 9 10 |
> y1999_s <- out1$mean$alpha + out2$mean$eps[0] > y2000_s <- out1$mean$alpha + out2$mean$eps[1] > y2001_s <- out1$mean$alpha + out2$mean$eps[2] > y2002_s <- out1$mean$alpha + out2$mean$eps[3] > y2003_s <- out1$mean$alpha + out2$mean$eps[4] > y2004_s <- out1$mean$alpha + out2$mean$eps[5] > y2005_s <- out1$mean$alpha + out2$mean$eps[6] > y2006_s <- out1$mean$alpha + out2$mean$eps[7] > y2007_s <- out1$mean$alpha + out2$mean$eps[8] > boxplot(exp(y1999_s), exp(y2000_s), exp(y2001_s), exp(y2002_s), exp(y2003_s), exp(y2004_s), exp(y2005_s), exp(y2006_s), exp(y2007_s), names=c(1999:2007)) |
次に固定効果の代わりに、ランダムサイト効果(年効果なし)を指定する。
この場合、alpha[j] ~ dnorm(mu.alpha, tau.alpha)で、平均mu.alpha、と標準偏差tau.alphaとその階層超パラメータsd.alpha
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281 282 |
> # (d) Random site effects (no year effects) > # Specify model in BUGS language > sink("GLMM1.txt") > cat(" + model { + + # Priors + for (j in 1:nsite){ + alpha[j] ~ dnorm(mu.alpha, tau.alpha) # Random site effects + } + mu.alpha ~ dnorm(0, 0.01) + tau.alpha <- 1/ (sd.alpha * sd.alpha) + sd.alpha ~ dunif(0, 5) + + # Likelihood + for (i in 1:nyear){ + for (j in 1:nsite){ + C[i,j] ~ dpois(lambda[i,j]) + lambda[i,j] <- exp(log.lambda[i,j]) + log.lambda[i,j] <- alpha[j] + } #j + } #i + } + ",fill = TRUE) > sink() > > # Bundle data > win.data <- list(C = t(C), nsite = nrow(C), nyear = ncol(C)) > > # Initial values > inits <- function() list(mu.alpha = runif(1, 2, 3)) > > # Parameters monitored > params <- c("alpha", "mu.alpha", "sd.alpha") > > # MCMC settings > ni <- 1200 > nt <- 2 > nb <- 200 > nc <- 3 > > # Call WinBUGS from R (BRT < 1 min) > out3 <- bugs(win.data, inits, params, "GLMM1.txt", n.chains = nc, + n.thin = nt, n.iter = ni, n.burnin = nb, debug = TRUE, bugs.directory = bugs.dir, working.directory = getwd()) > > # Summarize posteriors > print(out3, dig = 2) Inference for Bugs model at "GLMM1.txt", fit using WinBUGS, 3 chains, each with 1200 iterations (first 200 discarded), n.thin = 2 n.sims = 1500 iterations saved mean sd 2.5% 25% 50% 75% 97.5% Rhat alpha[1] -0.02 0.32 -0.68 -0.23 -0.01 0.19 0.60 1.00 alpha[2] -0.28 0.37 -1.09 -0.50 -0.26 -0.02 0.40 1.00 alpha[3] 2.46 0.10 2.27 2.39 2.46 2.53 2.64 1.00 alpha[4] 1.98 0.13 1.72 1.90 1.99 2.06 2.23 1.00 alpha[5] 3.09 0.07 2.94 3.05 3.10 3.14 3.22 1.00 alpha[6] -0.66 0.46 -1.63 -0.98 -0.62 -0.34 0.19 1.00 alpha[7] 0.84 0.24 0.36 0.69 0.86 1.00 1.28 1.00 alpha[8] 2.71 0.09 2.54 2.65 2.71 2.77 2.87 1.01 alpha[9] 0.28 0.30 -0.35 0.08 0.29 0.49 0.82 1.00 alpha[10] 1.75 0.14 1.48 1.66 1.76 1.85 2.00 1.00 alpha[11] 3.36 0.06 3.24 3.32 3.36 3.40 3.48 1.00 alpha[12] 3.55 0.06 3.45 3.52 3.55 3.59 3.66 1.00 alpha[13] 2.74 0.09 2.57 2.68 2.75 2.80 2.91 1.00 alpha[14] 1.77 0.14 1.48 1.68 1.77 1.87 2.03 1.00 alpha[15] 1.55 0.16 1.23 1.45 1.55 1.65 1.86 1.00 alpha[16] 2.51 0.09 2.33 2.45 2.51 2.58 2.69 1.00 alpha[17] 2.42 0.10 2.21 2.35 2.42 2.48 2.61 1.00 alpha[18] 2.71 0.09 2.54 2.65 2.71 2.77 2.88 1.00 alpha[19] 3.58 0.06 3.47 3.54 3.58 3.62 3.68 1.00 alpha[20] 2.61 0.09 2.44 2.55 2.61 2.67 2.80 1.00 alpha[21] 2.34 0.11 2.12 2.27 2.34 2.41 2.53 1.00 alpha[22] 1.95 0.13 1.69 1.86 1.96 2.04 2.22 1.00 alpha[23] 2.53 0.10 2.34 2.46 2.53 2.60 2.71 1.00 alpha[24] -0.57 0.40 -1.44 -0.84 -0.55 -0.29 0.16 1.00 alpha[25] 2.77 0.09 2.60 2.71 2.77 2.83 2.92 1.00 alpha[26] 2.17 0.11 1.95 2.10 2.17 2.25 2.38 1.00 alpha[27] 2.95 0.08 2.79 2.90 2.95 3.00 3.09 1.00 alpha[28] 3.64 0.05 3.53 3.60 3.64 3.68 3.75 1.00 alpha[29] 1.56 0.15 1.24 1.46 1.57 1.66 1.85 1.00 alpha[30] 0.25 0.28 -0.35 0.08 0.27 0.44 0.76 1.00 alpha[31] 1.55 0.16 1.24 1.45 1.56 1.66 1.84 1.00 alpha[32] 3.27 0.06 3.15 3.23 3.27 3.32 3.40 1.00 alpha[33] 4.18 0.04 4.10 4.15 4.18 4.20 4.25 1.00 alpha[34] 0.11 0.35 -0.62 -0.10 0.14 0.35 0.74 1.00 alpha[35] 3.60 0.06 3.49 3.56 3.60 3.64 3.71 1.00 alpha[36] 2.67 0.10 2.47 2.60 2.67 2.74 2.86 1.00 alpha[37] 3.46 0.06 3.35 3.42 3.46 3.50 3.58 1.00 alpha[38] -0.47 0.41 -1.33 -0.76 -0.46 -0.17 0.29 1.00 alpha[39] 2.57 0.09 2.38 2.50 2.57 2.63 2.75 1.00 alpha[40] 3.09 0.07 2.95 3.04 3.09 3.14 3.21 1.00 alpha[41] 1.97 0.13 1.70 1.89 1.97 2.06 2.22 1.00 alpha[42] 1.92 0.13 1.64 1.83 1.92 2.01 2.18 1.00 alpha[43] 3.00 0.07 2.86 2.95 3.00 3.05 3.14 1.00 alpha[44] 4.07 0.04 3.98 4.04 4.07 4.10 4.15 1.00 alpha[45] 3.38 0.06 3.25 3.34 3.38 3.42 3.49 1.00 alpha[46] 1.47 0.16 1.14 1.37 1.47 1.57 1.78 1.00 alpha[47] -0.97 0.49 -2.00 -1.28 -0.93 -0.63 -0.08 1.00 alpha[48] 3.26 0.07 3.12 3.21 3.26 3.30 3.38 1.00 alpha[49] 3.16 0.07 3.02 3.11 3.16 3.20 3.29 1.00 alpha[50] 3.00 0.08 2.86 2.95 3.00 3.05 3.15 1.00 alpha[51] 0.76 0.22 0.28 0.61 0.76 0.91 1.16 1.01 alpha[52] 2.82 0.08 2.66 2.76 2.82 2.88 2.98 1.00 alpha[53] 2.66 0.09 2.49 2.60 2.66 2.72 2.82 1.00 alpha[54] 2.46 0.10 2.26 2.40 2.46 2.53 2.65 1.00 alpha[55] 2.92 0.08 2.76 2.86 2.92 2.97 3.07 1.00 alpha[56] 0.71 0.24 0.22 0.56 0.72 0.87 1.15 1.00 alpha[57] 3.70 0.05 3.59 3.66 3.70 3.74 3.80 1.00 alpha[58] 3.11 0.07 2.98 3.06 3.11 3.15 3.25 1.00 alpha[59] 3.10 0.07 2.96 3.05 3.10 3.15 3.24 1.00 alpha[60] 1.14 0.19 0.75 1.01 1.15 1.27 1.50 1.00 alpha[61] 2.81 0.08 2.65 2.76 2.81 2.87 2.97 1.00 alpha[62] 2.25 0.11 2.04 2.18 2.25 2.33 2.46 1.00 alpha[63] 3.02 0.07 2.88 2.98 3.02 3.07 3.16 1.00 alpha[64] 3.16 0.07 3.03 3.12 3.16 3.21 3.29 1.00 alpha[65] 3.45 0.06 3.33 3.41 3.46 3.50 3.56 1.00 alpha[66] 0.25 0.28 -0.32 0.07 0.26 0.44 0.79 1.00 alpha[67] 3.51 0.06 3.40 3.47 3.51 3.55 3.63 1.00 alpha[68] 0.72 0.25 0.18 0.56 0.73 0.89 1.18 1.00 alpha[69] 2.65 0.09 2.48 2.59 2.65 2.71 2.83 1.00 alpha[70] 0.55 0.24 0.08 0.38 0.55 0.72 1.00 1.00 alpha[71] -0.01 0.33 -0.72 -0.23 0.00 0.21 0.57 1.00 alpha[72] 3.52 0.06 3.41 3.48 3.52 3.56 3.63 1.00 alpha[73] 2.68 0.09 2.50 2.62 2.68 2.74 2.84 1.00 alpha[74] 2.81 0.08 2.65 2.75 2.81 2.86 2.98 1.00 alpha[75] 0.47 0.26 -0.09 0.31 0.48 0.65 0.96 1.00 alpha[76] 1.20 0.19 0.81 1.07 1.21 1.33 1.54 1.00 alpha[77] 2.72 0.09 2.55 2.66 2.72 2.78 2.89 1.00 alpha[78] -1.00 0.52 -2.15 -1.30 -0.96 -0.65 -0.09 1.00 alpha[79] 3.32 0.07 3.18 3.27 3.32 3.36 3.45 1.00 alpha[80] 2.08 0.12 1.84 2.00 2.08 2.16 2.31 1.00 alpha[81] 2.81 0.09 2.63 2.75 2.82 2.88 2.99 1.00 alpha[82] 1.91 0.13 1.66 1.83 1.91 2.00 2.15 1.00 alpha[83] 2.30 0.10 2.10 2.23 2.31 2.38 2.51 1.00 alpha[84] 3.36 0.06 3.24 3.32 3.36 3.40 3.49 1.00 alpha[85] 2.64 0.09 2.47 2.58 2.64 2.71 2.81 1.00 alpha[86] 3.08 0.07 2.94 3.03 3.08 3.13 3.22 1.00 alpha[87] 3.48 0.06 3.35 3.44 3.48 3.52 3.60 1.00 alpha[88] 3.22 0.07 3.09 3.18 3.22 3.27 3.34 1.00 alpha[89] 3.15 0.07 3.02 3.11 3.16 3.20 3.29 1.00 alpha[90] 2.64 0.09 2.46 2.58 2.64 2.70 2.81 1.00 alpha[91] 1.63 0.15 1.34 1.52 1.63 1.73 1.90 1.00 alpha[92] 2.72 0.09 2.55 2.66 2.72 2.77 2.88 1.00 alpha[93] 2.54 0.09 2.35 2.48 2.54 2.61 2.71 1.00 alpha[94] 2.39 0.10 2.20 2.32 2.39 2.46 2.58 1.00 alpha[95] 1.56 0.16 1.23 1.45 1.56 1.67 1.87 1.00 alpha[96] 3.59 0.06 3.48 3.55 3.59 3.62 3.69 1.00 alpha[97] 2.79 0.09 2.61 2.73 2.79 2.85 2.95 1.00 alpha[98] 2.18 0.11 1.97 2.11 2.18 2.26 2.40 1.00 alpha[99] 3.66 0.05 3.55 3.62 3.66 3.69 3.76 1.00 alpha[100] 3.09 0.07 2.95 3.04 3.09 3.13 3.23 1.00 alpha[101] 2.46 0.10 2.27 2.39 2.46 2.52 2.64 1.00 alpha[102] 3.12 0.07 2.99 3.07 3.12 3.17 3.26 1.00 alpha[103] -0.97 0.49 -2.02 -1.30 -0.94 -0.62 -0.09 1.00 alpha[104] 3.42 0.06 3.30 3.38 3.42 3.45 3.53 1.00 alpha[105] 2.91 0.08 2.75 2.86 2.92 2.97 3.07 1.00 alpha[106] 2.14 0.11 1.92 2.07 2.15 2.22 2.36 1.00 alpha[107] -0.30 0.40 -1.19 -0.54 -0.27 -0.03 0.42 1.00 alpha[108] -1.01 0.50 -2.11 -1.32 -0.97 -0.66 -0.14 1.00 alpha[109] 1.69 0.14 1.41 1.60 1.70 1.79 1.97 1.00 alpha[110] 3.36 0.06 3.24 3.32 3.36 3.41 3.48 1.00 alpha[111] 2.57 0.09 2.39 2.51 2.57 2.63 2.74 1.00 n.eff alpha[1] 970 alpha[2] 500 alpha[3] 1500 alpha[4] 1500 alpha[5] 1500 alpha[6] 1500 alpha[7] 790 alpha[8] 390 alpha[9] 1500 alpha[10] 1500 alpha[11] 990 alpha[12] 1500 alpha[13] 1500 alpha[14] 1100 alpha[15] 1500 alpha[16] 830 alpha[17] 1500 alpha[18] 1500 alpha[19] 1000 alpha[20] 1500 alpha[21] 900 alpha[22] 1500 alpha[23] 1500 alpha[24] 1500 alpha[25] 1300 alpha[26] 1500 alpha[27] 1500 alpha[28] 1500 alpha[29] 1500 alpha[30] 910 alpha[31] 1500 alpha[32] 1500 alpha[33] 1500 alpha[34] 1500 alpha[35] 1500 alpha[36] 1500 alpha[37] 1300 alpha[38] 1500 alpha[39] 1500 alpha[40] 1500 alpha[41] 1500 alpha[42] 1300 alpha[43] 1500 alpha[44] 1500 alpha[45] 960 alpha[46] 1500 alpha[47] 1100 alpha[48] 840 alpha[49] 1500 alpha[50] 660 alpha[51] 1300 alpha[52] 1500 alpha[53] 1500 alpha[54] 1500 alpha[55] 1500 alpha[56] 1500 alpha[57] 1500 alpha[58] 1500 alpha[59] 1000 alpha[60] 1500 alpha[61] 1500 alpha[62] 880 alpha[63] 1200 alpha[64] 1500 alpha[65] 1500 alpha[66] 1500 alpha[67] 1500 alpha[68] 1500 alpha[69] 1500 alpha[70] 1500 alpha[71] 1500 alpha[72] 1500 alpha[73] 1500 alpha[74] 1500 alpha[75] 600 alpha[76] 1500 alpha[77] 1100 alpha[78] 1500 alpha[79] 1500 alpha[80] 530 alpha[81] 1200 alpha[82] 1500 alpha[83] 530 alpha[84] 910 alpha[85] 1500 alpha[86] 600 alpha[87] 1500 alpha[88] 1500 alpha[89] 1300 alpha[90] 1500 alpha[91] 1100 alpha[92] 1200 alpha[93] 1200 alpha[94] 700 alpha[95] 1500 alpha[96] 1500 alpha[97] 1100 alpha[98] 1500 alpha[99] 1500 alpha[100] 1500 alpha[101] 1500 alpha[102] 610 alpha[103] 1500 alpha[104] 700 alpha[105] 1500 alpha[106] 1500 alpha[107] 1500 alpha[108] 1500 alpha[109] 1500 alpha[110] 1500 alpha[111] 1400 [ reached getOption("max.print") -- omitted 127 rows ] For each parameter, n.eff is a crude measure of effective sample size, and Rhat is the potential scale reduction factor (at convergence, Rhat=1). DIC info (using the rule, pD = Dbar-Dhat) pD = 229.8 and DIC = 11922.8 DIC is an estimate of expected predictive error (lower deviance is better). |
パラメータalpha, mu.alpha, tau.alpha, sd.alphaがどうなったかを確認する。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 |
> out3$mean $alpha [1] -0.01533725 -0.25483459 2.45991400 1.98360400 3.08743000 -0.65058863 [7] 0.83555450 2.71034067 0.26367719 1.74810800 3.36067600 3.55211800 [13] 2.74362533 1.76068533 1.55458653 2.51811000 2.41051333 2.71100733 [19] 3.57593200 2.61440133 2.33991533 1.95824067 2.53557733 -0.57266770 [25] 2.76574400 2.17597800 2.94881333 3.63954467 1.55761133 0.24076148 [31] 1.56049133 3.27382267 4.17649400 0.08410081 3.59772200 2.67575533 [37] 3.46755867 -0.46578006 2.56406200 3.08569067 1.97035200 1.92505200 [43] 3.00518133 4.07136067 3.37550600 1.45734520 -0.98750235 3.25465067 [49] 3.15778000 2.99898467 0.76640529 2.81877667 2.65594133 2.46071133 [55] 2.91586933 0.71273128 3.69966133 3.10829867 3.09257667 1.14205260 [61] 2.81288600 2.24844400 3.02433467 3.15767133 3.45548467 0.25415669 [67] 3.51180733 0.70812681 2.65263200 0.54197365 -0.04309421 3.52114133 [73] 2.68258867 2.80702467 0.47426575 1.20383853 2.71743933 -1.01332955 [79] 3.31562333 2.08604933 2.82052667 1.91033600 2.30389400 3.35725000 [85] 2.63965267 3.07884400 3.48091867 3.22642133 3.15869200 2.63616667 [91] 1.62374067 2.71726067 2.54215600 2.39303533 1.56222727 3.58530467 [97] 2.78935333 2.17980000 3.65813733 3.08270867 2.45983000 3.12173200 [103] -0.98512439 3.41575000 2.91305200 2.14147533 -0.30363415 -0.99167881 [109] 1.69184600 3.36377533 2.56437400 3.49118867 2.78286533 2.17745067 [115] 1.92194067 3.14188000 0.75938742 2.14241933 2.42534467 2.68444600 [121] 2.96716667 2.08624600 0.18285495 -0.27685094 -0.97894368 2.86532867 [127] 2.56211400 -0.41601571 1.85729600 2.20105400 2.45141067 0.09470000 [133] 2.41320667 1.27309053 -0.58257942 2.64987333 3.68171267 2.55100400 [139] 1.68370667 2.47877600 2.96373933 3.12956333 -0.14875821 -0.76882749 [145] 2.53467800 3.18005133 2.28354200 2.13743400 3.34740800 1.41059320 [151] 3.39228733 3.41933200 2.01853600 1.55735887 1.93617800 2.03170600 [157] -0.39585732 1.03422447 2.95073533 -0.65669532 2.56454933 0.94349007 [163] 2.54624200 3.24646933 2.86492733 0.85416301 -0.56884591 0.32289811 [169] 1.29707460 3.05689000 2.00239133 3.01875667 3.23918600 0.47118377 [175] 2.50150133 1.55617933 -0.75664216 -0.30672701 2.56147867 0.05974794 [181] 2.07017867 2.89769133 0.58723572 1.41451113 2.08919600 2.13740000 [187] 3.41672800 3.23547667 3.33813200 2.15142133 3.28565467 2.68743600 [193] 3.40568600 1.98758067 2.19114533 2.67946400 0.53302566 3.61407733 [199] -1.30134617 3.22686267 2.80979067 0.25148036 2.80160533 1.74418467 [205] -0.40631645 2.03235733 3.24277733 2.58175333 2.95073800 2.03068933 [211] 3.53456933 2.53464667 3.05011200 0.25024972 2.51641733 3.09360600 [217] 2.92952267 3.24012800 2.65700267 3.14045600 1.13328927 -1.27686185 [223] 2.56118200 0.90348025 3.54951467 1.38773340 0.48260841 -0.40627552 [229] 2.80675000 3.33482200 3.75916533 3.66569800 3.67643200 3.36068933 [235] 3.59042267 $mu.alpha [1] 2.092945 $sd.alpha [1] 1.328842 $deviance [1] 11692.51 |
sd.alphaが1.328842なので、tau.alphaは、
> 1/(1.328842)^2
[1] 0.5663088
となる。
サイトに関するランダム効果は、正規分布normal(mu.alpha, tau.alpha)であるが、normal(2,092945, 0.5663088)となる。
サイトランダム効果alphaの頻度分布
> hist(exp(out3$mean$alpha))
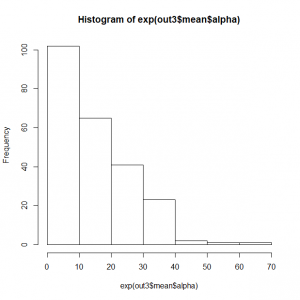
|
1 2 3 |
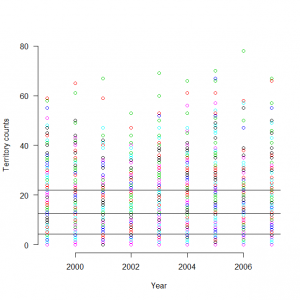
> quantile(exp(out3$mean$alpha)) 0% 25% 50% 75% 100% 0.2721652 4.2045089 12.6123690 21.9016223 65.1370818 |
|
1 2 3 4 |
> matplot(1999:2007, t(C), type = "p",pch=1, lty = 1, lwd = 1, main = "", las = 1, ylab = "Territory counts", xlab = "Year", ylim = c(0, 80), frame = FALSE) > abline(h=12.6123690) > abline(h= 4.2045089) > abline(h=21.9016223) |
次に、ランダムサイト効果、ランダム年効果を指定する。
モデルは、mu + alpha[j] + eps[i]
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281 282 283 284 285 286 287 288 289 |
> # (e) Random site and random year effects > # Specify model in BUGS language > sink("GLMM2.txt") > cat(" + model { + + # Priors + mu ~ dnorm(0, 0.01) # Grand mean + + for (j in 1:nsite){ + alpha[j] ~ dnorm(0, tau.alpha) # Random site effects + } + tau.alpha <- 1/ (sd.alpha * sd.alpha) + sd.alpha ~ dunif(0, 5) + + for (i in 1:nyear){ + eps[i] ~ dnorm(0, tau.eps) # Random year effects + } + tau.eps <- 1/ (sd.eps * sd.eps) + sd.eps ~ dunif(0, 3) + + # Likelihood + for (i in 1:nyear){ + for (j in 1:nsite){ + C[i,j] ~ dpois(lambda[i,j]) + lambda[i,j] <- exp(log.lambda[i,j]) + log.lambda[i,j] <- mu + alpha[j] + eps[i] + } #j + } #i + } + ",fill = TRUE) > sink() > > # Bundle data > win.data <- list(C = t(C), nsite = nrow(C), nyear = ncol(C)) > > # Initial values (not required for all) > inits <- function() list(mu = runif(1, 0, 4), alpha = runif(235, -2, 2), eps = runif(9, -1, 1)) > > # Parameters monitored > params <- c("mu", "alpha", "eps", "sd.alpha", "sd.eps") > > # MCMC settings > ni <- 6000 > nt <- 5 > nb <- 1000 > nc <- 3 > > # Call WinBUGS from R (BRT 3 min) > out4 <- bugs(win.data, inits, params, "GLMM2.txt", n.chains = nc, + n.thin = nt, n.iter = ni, n.burnin = nb, debug = TRUE, bugs.directory = bugs.dir, working.directory = getwd()) > > # Summarize posteriors > print(out4, dig = 2) Inference for Bugs model at "GLMM2.txt", fit using WinBUGS, 3 chains, each with 6000 iterations (first 1000 discarded), n.thin = 5 n.sims = 3000 iterations saved mean sd 2.5% 25% 50% 75% 97.5% Rhat mu 2.12 0.08 1.95 2.07 2.13 2.18 2.27 1.01 alpha[1] -2.14 0.33 -2.81 -2.36 -2.12 -1.91 -1.51 1.00 alpha[2] -2.38 0.37 -3.15 -2.61 -2.36 -2.12 -1.70 1.00 alpha[3] 0.34 0.13 0.09 0.25 0.34 0.42 0.59 1.00 alpha[4] -0.13 0.14 -0.41 -0.22 -0.12 -0.03 0.14 1.00 alpha[5] 0.98 0.10 0.77 0.91 0.97 1.04 1.19 1.00 alpha[6] -2.78 0.47 -3.77 -3.08 -2.73 -2.46 -1.96 1.00 alpha[7] -1.31 0.26 -1.81 -1.47 -1.30 -1.14 -0.82 1.00 alpha[8] 0.59 0.12 0.37 0.51 0.59 0.67 0.82 1.00 alpha[9] -1.84 0.32 -2.50 -2.04 -1.83 -1.62 -1.25 1.00 alpha[10] -0.37 0.16 -0.68 -0.47 -0.36 -0.26 -0.05 1.00 alpha[11] 1.24 0.10 1.06 1.18 1.24 1.31 1.44 1.01 alpha[12] 1.44 0.09 1.26 1.37 1.43 1.50 1.62 1.01 alpha[13] 0.63 0.11 0.42 0.55 0.63 0.70 0.85 1.00 alpha[14] -0.37 0.16 -0.71 -0.48 -0.37 -0.26 -0.05 1.00 alpha[15] -0.55 0.18 -0.90 -0.67 -0.55 -0.43 -0.21 1.00 alpha[16] 0.40 0.12 0.16 0.32 0.40 0.48 0.64 1.00 alpha[17] 0.30 0.12 0.05 0.21 0.30 0.38 0.53 1.01 alpha[18] 0.59 0.11 0.38 0.52 0.59 0.66 0.82 1.00 alpha[19] 1.46 0.09 1.28 1.40 1.46 1.52 1.64 1.01 alpha[20] 0.50 0.12 0.28 0.42 0.50 0.58 0.73 1.01 alpha[21] 0.22 0.13 -0.03 0.14 0.22 0.31 0.48 1.00 alpha[22] -0.15 0.15 -0.44 -0.25 -0.15 -0.05 0.15 1.00 alpha[23] 0.42 0.12 0.18 0.34 0.42 0.50 0.66 1.00 alpha[24] -2.69 0.42 -3.58 -2.97 -2.66 -2.39 -1.93 1.00 alpha[25] 0.65 0.11 0.43 0.57 0.65 0.73 0.87 1.00 alpha[26] 0.06 0.14 -0.20 -0.03 0.06 0.16 0.33 1.00 alpha[27] 0.84 0.11 0.64 0.76 0.84 0.91 1.05 1.00 alpha[28] 1.52 0.09 1.34 1.46 1.52 1.58 1.71 1.00 alpha[29] -0.56 0.17 -0.89 -0.67 -0.56 -0.44 -0.22 1.00 alpha[30] -1.86 0.29 -2.48 -2.05 -1.85 -1.66 -1.31 1.00 alpha[31] -0.55 0.17 -0.90 -0.67 -0.55 -0.43 -0.23 1.00 alpha[32] 1.15 0.10 0.97 1.09 1.15 1.22 1.35 1.01 alpha[33] 2.06 0.09 1.90 2.00 2.06 2.12 2.25 1.01 alpha[34] -2.05 0.35 -2.77 -2.27 -2.03 -1.80 -1.42 1.00 alpha[35] 1.48 0.09 1.31 1.42 1.48 1.54 1.67 1.01 alpha[36] 0.55 0.12 0.30 0.46 0.54 0.63 0.79 1.00 alpha[37] 1.35 0.09 1.17 1.28 1.35 1.41 1.54 1.00 alpha[38] -2.59 0.43 -3.50 -2.87 -2.55 -2.27 -1.82 1.00 alpha[39] 0.45 0.11 0.22 0.37 0.45 0.52 0.67 1.00 alpha[40] 0.97 0.10 0.77 0.90 0.97 1.04 1.17 1.01 alpha[41] -0.14 0.15 -0.44 -0.24 -0.14 -0.04 0.13 1.01 alpha[42] -0.21 0.16 -0.52 -0.32 -0.20 -0.10 0.08 1.00 alpha[43] 0.89 0.11 0.68 0.82 0.88 0.96 1.10 1.00 alpha[44] 1.96 0.09 1.79 1.90 1.95 2.01 2.13 1.01 alpha[45] 1.26 0.10 1.07 1.19 1.26 1.32 1.46 1.00 alpha[46] -0.65 0.17 -1.00 -0.77 -0.65 -0.54 -0.32 1.00 alpha[47] -3.12 0.52 -4.26 -3.44 -3.08 -2.75 -2.22 1.00 alpha[48] 1.14 0.10 0.96 1.08 1.14 1.21 1.33 1.00 alpha[49] 1.04 0.10 0.84 0.97 1.04 1.11 1.25 1.01 alpha[50] 0.89 0.10 0.69 0.81 0.88 0.95 1.10 1.00 alpha[51] -1.35 0.24 -1.83 -1.51 -1.34 -1.18 -0.92 1.00 alpha[52] 0.70 0.11 0.49 0.63 0.70 0.78 0.92 1.00 alpha[53] 0.54 0.11 0.33 0.47 0.54 0.62 0.76 1.00 alpha[54] 0.35 0.12 0.11 0.27 0.35 0.43 0.59 1.00 alpha[55] 0.80 0.11 0.60 0.73 0.80 0.87 1.02 1.01 alpha[56] -1.37 0.26 -1.89 -1.54 -1.36 -1.19 -0.88 1.00 alpha[57] 1.59 0.09 1.42 1.52 1.58 1.64 1.78 1.01 alpha[58] 0.99 0.10 0.80 0.92 0.99 1.06 1.21 1.01 alpha[59] 0.98 0.10 0.78 0.91 0.98 1.05 1.19 1.00 alpha[60] -0.97 0.21 -1.38 -1.12 -0.97 -0.83 -0.57 1.00 alpha[61] 0.70 0.11 0.49 0.62 0.70 0.77 0.92 1.00 alpha[62] 0.13 0.13 -0.12 0.04 0.14 0.22 0.39 1.00 alpha[63] 0.91 0.10 0.70 0.84 0.91 0.98 1.12 1.01 alpha[64] 1.04 0.10 0.85 0.97 1.04 1.11 1.25 1.00 alpha[65] 1.34 0.10 1.16 1.27 1.34 1.40 1.54 1.00 alpha[66] -1.86 0.30 -2.47 -2.04 -1.84 -1.66 -1.29 1.00 alpha[67] 1.40 0.09 1.22 1.33 1.39 1.46 1.59 1.01 alpha[68] -1.41 0.26 -1.93 -1.58 -1.40 -1.23 -0.93 1.00 alpha[69] 0.53 0.12 0.30 0.46 0.53 0.61 0.77 1.01 alpha[70] -1.58 0.26 -2.12 -1.74 -1.57 -1.40 -1.10 1.00 alpha[71] -2.14 0.34 -2.84 -2.37 -2.13 -1.91 -1.52 1.00 alpha[72] 1.41 0.09 1.22 1.34 1.40 1.47 1.60 1.01 alpha[73] 0.56 0.11 0.34 0.49 0.56 0.64 0.79 1.00 alpha[74] 0.69 0.11 0.48 0.61 0.69 0.76 0.91 1.00 alpha[75] -1.65 0.27 -2.21 -1.82 -1.64 -1.46 -1.15 1.00 alpha[76] -0.91 0.19 -1.29 -1.03 -0.91 -0.78 -0.54 1.00 alpha[77] 0.60 0.12 0.37 0.52 0.60 0.68 0.83 1.00 alpha[78] -3.11 0.52 -4.23 -3.43 -3.06 -2.76 -2.19 1.00 alpha[79] 1.21 0.10 1.02 1.14 1.20 1.27 1.42 1.01 alpha[80] -0.03 0.14 -0.30 -0.13 -0.03 0.07 0.25 1.00 alpha[81] 0.67 0.12 0.44 0.59 0.67 0.75 0.90 1.00 alpha[82] -0.21 0.15 -0.50 -0.31 -0.21 -0.11 0.08 1.01 alpha[83] 0.19 0.13 -0.06 0.11 0.19 0.28 0.44 1.00 alpha[84] 1.24 0.10 1.05 1.18 1.24 1.31 1.44 1.01 alpha[85] 0.52 0.12 0.30 0.44 0.52 0.60 0.75 1.00 alpha[86] 0.97 0.10 0.77 0.90 0.97 1.03 1.17 1.00 alpha[87] 1.37 0.10 1.18 1.30 1.37 1.43 1.56 1.00 alpha[88] 1.11 0.10 0.92 1.04 1.11 1.17 1.31 1.01 alpha[89] 1.04 0.10 0.85 0.97 1.04 1.11 1.25 1.00 alpha[90] 0.53 0.11 0.30 0.45 0.52 0.60 0.75 1.00 alpha[91] -0.49 0.17 -0.82 -0.60 -0.49 -0.38 -0.18 1.00 alpha[92] 0.60 0.11 0.38 0.52 0.60 0.67 0.82 1.00 alpha[93] 0.42 0.12 0.19 0.34 0.42 0.50 0.66 1.00 alpha[94] 0.27 0.12 0.04 0.19 0.28 0.36 0.52 1.00 alpha[95] -0.56 0.17 -0.89 -0.66 -0.56 -0.44 -0.23 1.01 alpha[96] 1.47 0.09 1.30 1.41 1.47 1.53 1.66 1.01 alpha[97] 0.67 0.11 0.44 0.59 0.67 0.75 0.90 1.00 alpha[98] 0.06 0.13 -0.21 -0.02 0.06 0.15 0.33 1.00 alpha[99] 1.54 0.09 1.36 1.48 1.54 1.60 1.73 1.01 alpha[100] 0.97 0.11 0.77 0.90 0.97 1.04 1.19 1.00 alpha[101] 0.35 0.12 0.10 0.26 0.35 0.43 0.58 1.00 alpha[102] 1.01 0.10 0.82 0.94 1.01 1.08 1.22 1.00 alpha[103] -3.12 0.51 -4.21 -3.43 -3.09 -2.76 -2.22 1.00 alpha[104] 1.30 0.10 1.11 1.24 1.30 1.36 1.50 1.00 alpha[105] 0.80 0.11 0.58 0.72 0.79 0.87 1.01 1.01 alpha[106] 0.02 0.14 -0.25 -0.07 0.03 0.12 0.29 1.00 alpha[107] -2.43 0.40 -3.25 -2.69 -2.41 -2.16 -1.68 1.00 alpha[108] -3.10 0.52 -4.23 -3.42 -3.06 -2.74 -2.20 1.00 alpha[109] -0.42 0.16 -0.73 -0.52 -0.42 -0.32 -0.12 1.00 alpha[110] 1.24 0.10 1.06 1.18 1.24 1.31 1.45 1.01 n.eff mu 310 alpha[1] 3000 alpha[2] 3000 alpha[3] 1100 alpha[4] 1100 alpha[5] 940 alpha[6] 3000 alpha[7] 3000 alpha[8] 1700 alpha[9] 3000 alpha[10] 2700 alpha[11] 500 alpha[12] 420 alpha[13] 860 alpha[14] 3000 alpha[15] 3000 alpha[16] 950 alpha[17] 450 alpha[18] 1000 alpha[19] 500 alpha[20] 590 alpha[21] 690 alpha[22] 990 alpha[23] 880 alpha[24] 640 alpha[25] 1400 alpha[26] 470 alpha[27] 1000 alpha[28] 580 alpha[29] 880 alpha[30] 2200 alpha[31] 950 alpha[32] 710 alpha[33] 630 alpha[34] 2000 alpha[35] 430 alpha[36] 710 alpha[37] 780 alpha[38] 3000 alpha[39] 3000 alpha[40] 410 alpha[41] 340 alpha[42] 790 alpha[43] 810 alpha[44] 310 alpha[45] 620 alpha[46] 3000 alpha[47] 1400 alpha[48] 650 alpha[49] 300 alpha[50] 570 alpha[51] 600 alpha[52] 790 alpha[53] 700 alpha[54] 650 alpha[55] 320 alpha[56] 3000 alpha[57] 410 alpha[58] 370 alpha[59] 720 alpha[60] 1300 alpha[61] 660 alpha[62] 1400 alpha[63] 640 alpha[64] 650 alpha[65] 560 alpha[66] 2500 alpha[67] 460 alpha[68] 1600 alpha[69] 390 alpha[70] 2700 alpha[71] 1700 alpha[72] 280 alpha[73] 780 alpha[74] 650 alpha[75] 700 alpha[76] 1700 alpha[77] 550 alpha[78] 530 alpha[79] 420 alpha[80] 530 alpha[81] 3000 alpha[82] 390 alpha[83] 870 alpha[84] 450 alpha[85] 730 alpha[86] 670 alpha[87] 610 alpha[88] 410 alpha[89] 510 alpha[90] 1100 alpha[91] 1400 alpha[92] 510 alpha[93] 2200 alpha[94] 1000 alpha[95] 420 alpha[96] 460 alpha[97] 790 alpha[98] 3000 alpha[99] 430 alpha[100] 680 alpha[101] 830 alpha[102] 940 alpha[103] 1800 alpha[104] 470 alpha[105] 570 alpha[106] 570 alpha[107] 3000 alpha[108] 3000 alpha[109] 3000 alpha[110] 380 [ reached getOption("max.print") -- omitted 137 rows ] For each parameter, n.eff is a crude measure of effective sample size, and Rhat is the potential scale reduction factor (at convergence, Rhat=1). DIC info (using the rule, pD = Dbar-Dhat) pD = 238.0 and DIC = 11479.5 DIC is an estimate of expected predictive error (lower deviance is better). |
out4の結果を分析してみる。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 |
> out4$mean $mu [1] 2.079934 $alpha [1] -2.1076160000 -2.3545093333 0.3751784247 -0.0984386457 1.0117119667 [6] -2.7426016667 -1.2722481667 0.6290491000 -1.8041110667 -0.3334423581 [11] 1.2776041333 1.4716913333 0.6638995000 -0.3316310800 -0.5219901773 [16] 0.4376290920 0.3309014903 0.6258340000 1.4953263333 0.5365536000 [21] 0.2569850564 -0.1067241607 0.4524984760 -2.6553843333 0.6851756333 [26] 0.1011082043 0.8702921000 1.5584740000 -0.5210529813 -1.8374272333 [31] -0.5172678170 1.1925051000 2.0971663333 -2.0156803333 1.5172503333 [36] 0.5815341567 1.3847936667 -2.5509730000 0.4860883400 1.0044183667 [41] -0.1149639381 -0.1809190222 0.9218477333 1.9897960000 1.2954192333 [46] -0.6179790767 -3.0743640000 1.1765601000 1.0785564000 0.9208005667 [51] -1.3141167000 0.7389478000 0.5762309000 0.3779662058 0.8343946667 [56] -1.3364468333 1.6224210000 1.0303545333 1.0165552667 -0.9413371333 [61] 0.7309692000 0.1710958487 0.9433328667 1.0801161000 1.3741570000 [66] -1.8304656667 1.4331556667 -1.3692234667 0.5680491333 -1.5452493000 [71] -2.1153153333 1.4399076667 0.6005449333 0.7269949333 -1.6066126333 [76] -0.8761065533 0.6366652667 -3.0903596667 1.2442758000 0.0063760463 [81] 0.7061618333 -0.1762970090 0.2235286068 1.2789878333 0.5588846667 [86] 0.9991912333 1.4022243333 1.1422687333 1.0787838333 0.5608177033 [91] -0.4528720143 0.6340963667 0.4599763233 0.3121647289 -0.5274245900 [96] 1.5048220000 0.7055925000 0.0960184140 1.5761736667 1.0060722667 [101] 0.3778606759 1.0448842333 -3.0750446667 1.3337299333 0.8297113000 [106] 0.0624435267 -2.3842036667 -3.0836513333 -0.3925182080 1.2829311667 [111] 0.4872490100 1.4112093333 0.7004724000 0.0940167048 -0.1538368739 [116] 1.0600331000 -1.3133232667 0.0574847059 0.3177391546 0.6007570333 [121] 0.8875548333 0.0062407210 -1.9186790000 -2.3564910000 -3.0848003333 [126] 0.7630713667 0.4794156700 -2.4906266667 -0.2246371851 0.1215710147 [131] 0.3711607637 -2.0100346667 0.3331621467 -0.8154101000 -2.6595820000 [136] 0.5663238000 1.6012320000 0.4664238067 -0.3920611097 0.3991698107 [141] 0.8802210667 1.0505269667 -2.2329366667 -2.8376356667 0.4507405133 [146] 1.1030347667 0.2028010757 0.0580259607 1.2652343667 -0.6707134367 [151] 1.3082605333 1.3406847000 -0.0674420304 -0.5236424237 -0.1402735253 [156] -0.0485068804 -2.4839703333 -1.0550641667 0.8693103000 -2.7530903333 [161] 0.4886674733 -1.1371263000 0.4706723233 1.1709639667 0.7846504667 [166] -1.2228740667 -2.6560760000 -1.7564072667 -0.7843870333 0.9741382333 [171] -0.0787713362 0.9382541333 1.1588118667 -1.6077497667 0.4257994027 [176] -0.5320175540 -2.8471593333 -2.3876526667 0.4780909833 -2.0132366667 [181] -0.0224946329 0.8170963667 -1.4903307333 -0.6725187500 0.0002735269 [186] 0.0615285808 1.3355770000 1.1549789333 1.2540017000 0.0616946154 [191] 1.2071309333 0.6062342633 1.3229721667 -0.0934144066 0.1088368608 [196] 0.5962894000 -1.5499949667 1.5353040000 -3.3432026667 1.1474043667 [201] 0.7259523667 -1.8305562333 0.7120414667 -0.3306824111 -2.4851983333 [206] -0.0489758090 1.1645877000 0.5020208667 0.8698751333 -0.0625316114 [211] 1.4539290000 0.4534100500 0.9690620667 -1.8343858333 0.4377375067 [216] 1.0084791667 0.8493568000 1.1608506667 0.5755300733 1.0593044000 [221] -0.9435206000 -3.3489493333 0.4749199933 -1.1803739667 1.4680206667 [226] -0.6889885667 -1.6056878333 -2.4965093333 0.7285914667 1.2559645000 [231] 1.6771703333 1.5841696667 1.5941433333 1.2796602333 1.5100196667 $eps [1] -0.002253751 0.071110502 -0.160016563 -0.108322322 0.054035349 0.094344020 [7] 0.216188823 -0.161350977 -0.067930269 $sd.alpha [1] 1.329022 $sd.eps [1] 0.1589848 $deviance [1] 11240.39 |
tau.alphaは、
|
1 2 |
> 1/(out4$mean$sd.alpha)^2 [1] 0.5661551 |
μ=2.079934
alpha = サイトランダム要因
年ランダム要因epsは、
[1] -0.002253751 0.071110502 -0.160016563 -0.108322322 0.054035349 0.094344020
[7] 0.216188823 -0.161350977 -0.067930269
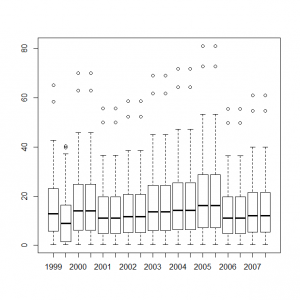
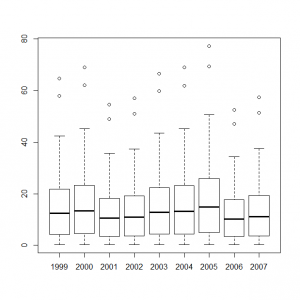
これらのデータをまとめて、統計モデル化した年ごとの計測数値のボックスプロットを作成すると、
|
1 2 3 4 5 6 7 8 9 10 |
> y1999_t <- out4$mean$alpha + out4$mean$mu + out4$mean$eps[1] > y2000_t <- out4$mean$alpha + out4$mean$mu + out4$mean$eps[2] > y2001_t <- out4$mean$alpha + out4$mean$mu + out4$mean$eps[3] > y2002_t <- out4$mean$alpha + out4$mean$mu + out4$mean$eps[4] > y2003_t <- out4$mean$alpha + out4$mean$mu + out4$mean$eps[5] > y2004_t <- out4$mean$alpha + out4$mean$mu + out4$mean$eps[6] > y2005_t <- out4$mean$alpha + out4$mean$mu + out4$mean$eps[7] > y2006_t <- out4$mean$alpha + out4$mean$mu + out4$mean$eps[8] > y2007_t <- out4$mean$alpha + out4$mean$mu + out4$mean$eps[9] > boxplot(exp(y1999_t), exp(y2000_t), exp(y2001_t), exp(y2002_t), exp(y2003_t), exp(y2004_t), exp(y2005_t), exp(y2006_t), exp(y2007_t), names=c(1999:2007)) |
次に初年観察者効果を固定効果として追加する。
モデルは mu + beta2 * first[i,j] + alpha[j] + eps[i]
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281 282 283 284 285 286 287 288 289 290 |
> # (f) Random site and random year effects and first-year fixed observer effect > # Specify model in BUGS language > sink("GLMM3.txt") > cat(" + model { + + # Priors + mu ~ dnorm(0, 0.01) # Overall mean + beta2 ~ dnorm(0, 0.01) # First-year observer effect + + for (j in 1:nsite){ + alpha[j] ~ dnorm(0, tau.alpha) # Random site effects + } + tau.alpha <- 1/ (sd.alpha * sd.alpha) + sd.alpha ~ dunif(0, 5) + + for (i in 1:nyear){ + eps[i] ~ dnorm(0, tau.eps) # Random year effects + } + tau.eps <- 1/ (sd.eps * sd.eps) + sd.eps ~ dunif(0, 5) + + # Likelihood + for (i in 1:nyear){ + for (j in 1:nsite){ + C[i,j] ~ dpois(lambda[i,j]) + lambda[i,j] <- exp(log.lambda[i,j]) + log.lambda[i,j] <- mu + beta2 * first[i,j] + alpha[j] + eps[i] + } #j + } #i + } + ",fill = TRUE) > sink() > > # Bundle data > win.data <- list(C = t(C), nsite = nrow(C), nyear = ncol(C), first = t(first)) > > # Initial values > inits <- function() list(mu = runif(1, 0, 4), beta2 = runif(1, -1, 1), alpha = runif(235, -2, 2), eps = runif(9, -1, 1)) > > # Parameters monitored > params <- c("mu", "beta2", "alpha", "eps", "sd.alpha", "sd.eps") > > # MCMC settings > ni <- 6000 > nt <- 5 > nb <- 1000 > nc <- 3 > > # Call WinBUGS from R (BRT 3 min) > out5 <- bugs(win.data, inits, params, "GLMM3.txt", n.chains = nc, + n.thin = nt, n.iter = ni, n.burnin = nb, debug = TRUE, bugs.directory = bugs.dir, working.directory = getwd()) > > # Summarize posteriors > print(out5, dig = 2) Inference for Bugs model at "GLMM3.txt", fit using WinBUGS, 3 chains, each with 6000 iterations (first 1000 discarded), n.thin = 5 n.sims = 3000 iterations saved mean sd 2.5% 25% 50% 75% 97.5% Rhat mu 2.10 0.12 1.86 2.03 2.10 2.18 2.35 1.29 beta2 0.00 0.02 -0.04 -0.02 0.00 0.01 0.04 1.00 alpha[1] -2.12 0.34 -2.85 -2.34 -2.10 -1.89 -1.52 1.01 alpha[2] -2.35 0.38 -3.17 -2.60 -2.33 -2.09 -1.67 1.01 alpha[3] 0.36 0.13 0.10 0.28 0.36 0.45 0.64 1.07 alpha[4] -0.11 0.15 -0.42 -0.22 -0.12 -0.01 0.17 1.05 alpha[5] 0.99 0.11 0.77 0.92 0.99 1.06 1.24 1.12 alpha[6] -2.76 0.47 -3.79 -3.07 -2.73 -2.45 -1.91 1.01 alpha[7] -1.29 0.26 -1.82 -1.46 -1.28 -1.11 -0.80 1.02 alpha[8] 0.61 0.12 0.37 0.53 0.61 0.69 0.86 1.11 alpha[9] -1.81 0.32 -2.45 -2.02 -1.80 -1.60 -1.23 1.01 alpha[10] -0.35 0.16 -0.68 -0.46 -0.34 -0.24 -0.03 1.04 alpha[11] 1.26 0.10 1.07 1.19 1.26 1.33 1.48 1.11 alpha[12] 1.45 0.10 1.25 1.39 1.45 1.52 1.67 1.12 alpha[13] 0.65 0.12 0.41 0.57 0.65 0.72 0.89 1.08 alpha[14] -0.35 0.17 -0.71 -0.47 -0.35 -0.24 -0.02 1.04 alpha[15] -0.53 0.18 -0.90 -0.65 -0.53 -0.41 -0.17 1.04 alpha[16] 0.42 0.13 0.16 0.33 0.42 0.50 0.67 1.09 alpha[17] 0.31 0.13 0.06 0.23 0.31 0.40 0.57 1.07 alpha[18] 0.61 0.12 0.38 0.53 0.60 0.69 0.87 1.08 alpha[19] 1.48 0.10 1.28 1.41 1.48 1.54 1.70 1.14 alpha[20] 0.52 0.12 0.28 0.44 0.52 0.60 0.78 1.07 alpha[21] 0.24 0.14 -0.03 0.15 0.24 0.33 0.50 1.07 alpha[22] -0.13 0.16 -0.44 -0.24 -0.13 -0.02 0.19 1.05 alpha[23] 0.43 0.13 0.18 0.35 0.43 0.52 0.70 1.10 alpha[24] -2.67 0.42 -3.57 -2.94 -2.66 -2.39 -1.90 1.01 alpha[25] 0.67 0.12 0.43 0.59 0.67 0.75 0.91 1.09 alpha[26] 0.08 0.14 -0.19 -0.02 0.08 0.17 0.37 1.07 alpha[27] 0.85 0.12 0.63 0.77 0.85 0.93 1.09 1.10 alpha[28] 1.54 0.10 1.35 1.47 1.54 1.60 1.76 1.11 alpha[29] -0.54 0.17 -0.89 -0.65 -0.54 -0.43 -0.19 1.04 alpha[30] -1.85 0.30 -2.47 -2.05 -1.84 -1.64 -1.28 1.01 alpha[31] -0.53 0.17 -0.88 -0.65 -0.54 -0.42 -0.20 1.05 alpha[32] 1.18 0.11 0.96 1.11 1.17 1.24 1.41 1.11 alpha[33] 2.08 0.09 1.90 2.02 2.08 2.13 2.30 1.15 alpha[34] -2.03 0.35 -2.75 -2.25 -2.00 -1.80 -1.36 1.01 alpha[35] 1.50 0.10 1.30 1.43 1.50 1.56 1.72 1.13 alpha[36] 0.56 0.13 0.31 0.47 0.56 0.64 0.83 1.08 alpha[37] 1.37 0.11 1.16 1.30 1.36 1.43 1.58 1.14 alpha[38] -2.56 0.44 -3.50 -2.84 -2.54 -2.25 -1.77 1.01 alpha[39] 0.47 0.13 0.21 0.39 0.47 0.55 0.72 1.08 alpha[40] 0.99 0.11 0.77 0.91 0.98 1.06 1.21 1.11 alpha[41] -0.13 0.15 -0.42 -0.23 -0.13 -0.03 0.16 1.05 alpha[42] -0.20 0.16 -0.51 -0.31 -0.20 -0.09 0.11 1.04 alpha[43] 0.90 0.12 0.67 0.83 0.90 0.98 1.15 1.11 alpha[44] 1.97 0.10 1.79 1.91 1.97 2.03 2.19 1.14 alpha[45] 1.27 0.11 1.07 1.20 1.27 1.34 1.50 1.12 alpha[46] -0.64 0.18 -1.01 -0.76 -0.63 -0.51 -0.28 1.02 alpha[47] -3.09 0.51 -4.19 -3.40 -3.05 -2.73 -2.18 1.01 alpha[48] 1.16 0.11 0.95 1.09 1.16 1.23 1.40 1.12 alpha[49] 1.06 0.11 0.85 0.99 1.06 1.13 1.29 1.10 alpha[50] 0.90 0.11 0.68 0.83 0.90 0.98 1.14 1.09 alpha[51] -1.34 0.24 -1.83 -1.50 -1.34 -1.18 -0.89 1.01 alpha[52] 0.72 0.12 0.48 0.64 0.72 0.80 0.98 1.08 alpha[53] 0.56 0.12 0.32 0.48 0.55 0.63 0.81 1.08 alpha[54] 0.36 0.13 0.12 0.27 0.36 0.45 0.62 1.06 alpha[55] 0.81 0.12 0.58 0.73 0.81 0.89 1.05 1.10 alpha[56] -1.36 0.26 -1.91 -1.53 -1.35 -1.18 -0.86 1.01 alpha[57] 1.60 0.10 1.41 1.53 1.60 1.66 1.82 1.13 alpha[58] 1.01 0.11 0.79 0.94 1.01 1.08 1.24 1.12 alpha[59] 1.00 0.11 0.79 0.93 1.00 1.07 1.23 1.10 alpha[60] -0.96 0.21 -1.39 -1.10 -0.96 -0.83 -0.54 1.02 alpha[61] 0.72 0.12 0.49 0.64 0.72 0.80 0.96 1.07 alpha[62] 0.15 0.14 -0.12 0.06 0.15 0.24 0.43 1.06 alpha[63] 0.92 0.12 0.71 0.85 0.92 1.00 1.17 1.10 alpha[64] 1.06 0.11 0.85 0.99 1.06 1.13 1.29 1.11 alpha[65] 1.36 0.11 1.15 1.29 1.35 1.42 1.58 1.12 alpha[66] -1.85 0.30 -2.46 -2.04 -1.84 -1.65 -1.30 1.01 alpha[67] 1.41 0.10 1.21 1.35 1.41 1.48 1.64 1.12 alpha[68] -1.39 0.26 -1.92 -1.57 -1.38 -1.22 -0.92 1.01 alpha[69] 0.55 0.12 0.31 0.47 0.54 0.62 0.81 1.09 alpha[70] -1.56 0.26 -2.11 -1.72 -1.55 -1.39 -1.07 1.02 alpha[71] -2.12 0.34 -2.84 -2.34 -2.10 -1.88 -1.51 1.01 alpha[72] 1.42 0.11 1.23 1.35 1.42 1.49 1.65 1.13 alpha[73] 0.58 0.12 0.33 0.50 0.58 0.66 0.83 1.09 alpha[74] 0.71 0.12 0.48 0.63 0.71 0.79 0.96 1.08 alpha[75] -1.62 0.28 -2.18 -1.80 -1.61 -1.43 -1.10 1.02 alpha[76] -0.89 0.19 -1.29 -1.02 -0.88 -0.76 -0.51 1.03 alpha[77] 0.62 0.12 0.37 0.53 0.62 0.70 0.87 1.09 alpha[78] -3.10 0.51 -4.23 -3.40 -3.06 -2.74 -2.18 1.01 alpha[79] 1.23 0.11 1.02 1.15 1.22 1.30 1.47 1.09 alpha[80] -0.01 0.15 -0.30 -0.11 -0.01 0.08 0.28 1.05 alpha[81] 0.69 0.13 0.45 0.61 0.69 0.77 0.94 1.09 alpha[82] -0.19 0.16 -0.49 -0.30 -0.19 -0.09 0.10 1.04 alpha[83] 0.21 0.14 -0.06 0.12 0.21 0.30 0.47 1.06 alpha[84] 1.26 0.11 1.06 1.19 1.26 1.33 1.49 1.11 alpha[85] 0.54 0.12 0.30 0.46 0.54 0.62 0.79 1.10 alpha[86] 0.98 0.11 0.77 0.91 0.98 1.05 1.21 1.11 alpha[87] 1.38 0.11 1.18 1.31 1.38 1.45 1.59 1.12 alpha[88] 1.12 0.11 0.92 1.05 1.12 1.19 1.35 1.10 alpha[89] 1.06 0.11 0.85 0.99 1.06 1.13 1.29 1.11 alpha[90] 0.54 0.12 0.31 0.46 0.54 0.62 0.79 1.09 alpha[91] -0.47 0.17 -0.80 -0.58 -0.46 -0.35 -0.14 1.03 alpha[92] 0.62 0.12 0.38 0.54 0.62 0.70 0.87 1.11 alpha[93] 0.44 0.13 0.20 0.36 0.44 0.53 0.70 1.07 alpha[94] 0.30 0.13 0.04 0.21 0.29 0.38 0.56 1.08 alpha[95] -0.54 0.17 -0.87 -0.65 -0.53 -0.42 -0.20 1.04 alpha[96] 1.49 0.10 1.28 1.42 1.48 1.55 1.71 1.12 alpha[97] 0.69 0.12 0.46 0.61 0.69 0.77 0.94 1.08 alpha[98] 0.08 0.14 -0.20 -0.02 0.08 0.17 0.37 1.06 alpha[99] 1.56 0.10 1.36 1.49 1.55 1.62 1.78 1.12 alpha[100] 0.99 0.11 0.78 0.92 0.99 1.06 1.22 1.12 alpha[101] 0.36 0.13 0.11 0.27 0.36 0.45 0.63 1.07 alpha[102] 1.03 0.11 0.82 0.95 1.02 1.09 1.27 1.10 alpha[103] -3.07 0.52 -4.19 -3.39 -3.03 -2.71 -2.16 1.01 alpha[104] 1.32 0.10 1.12 1.25 1.32 1.38 1.53 1.13 alpha[105] 0.81 0.12 0.58 0.73 0.81 0.89 1.05 1.08 alpha[106] 0.04 0.14 -0.24 -0.05 0.04 0.14 0.31 1.06 alpha[107] -2.41 0.40 -3.29 -2.66 -2.39 -2.13 -1.68 1.01 alpha[108] -3.08 0.50 -4.16 -3.41 -3.05 -2.73 -2.19 1.00 alpha[109] -0.41 0.16 -0.73 -0.52 -0.41 -0.30 -0.09 1.03 n.eff mu 11 beta2 1500 alpha[1] 190 alpha[2] 220 alpha[3] 34 alpha[4] 43 alpha[5] 22 alpha[6] 340 alpha[7] 110 alpha[8] 26 alpha[9] 140 alpha[10] 55 alpha[11] 22 alpha[12] 22 alpha[13] 32 alpha[14] 57 alpha[15] 54 alpha[16] 35 alpha[17] 33 alpha[18] 32 alpha[19] 19 alpha[20] 39 alpha[21] 33 alpha[22] 49 alpha[23] 31 alpha[24] 280 alpha[25] 28 alpha[26] 35 alpha[27] 27 alpha[28] 22 alpha[29] 53 alpha[30] 170 alpha[31] 45 alpha[32] 23 alpha[33] 18 alpha[34] 170 alpha[35] 20 alpha[36] 31 alpha[37] 19 alpha[38] 340 alpha[39] 29 alpha[40] 23 alpha[41] 42 alpha[42] 61 alpha[43] 24 alpha[44] 19 alpha[45] 21 alpha[46] 100 alpha[47] 410 alpha[48] 21 alpha[49] 25 alpha[50] 29 alpha[51] 210 alpha[52] 30 alpha[53] 33 alpha[54] 36 alpha[55] 27 alpha[56] 140 alpha[57] 20 alpha[58] 21 alpha[59] 25 alpha[60] 98 alpha[61] 33 alpha[62] 37 alpha[63] 25 alpha[64] 24 alpha[65] 22 alpha[66] 210 alpha[67] 21 alpha[68] 160 alpha[69] 30 alpha[70] 140 alpha[71] 240 alpha[72] 20 alpha[73] 30 alpha[74] 30 alpha[75] 100 alpha[76] 73 alpha[77] 28 alpha[78] 390 alpha[79] 26 alpha[80] 47 alpha[81] 28 alpha[82] 51 alpha[83] 36 alpha[84] 22 alpha[85] 27 alpha[86] 23 alpha[87] 21 alpha[88] 24 alpha[89] 22 alpha[90] 32 alpha[91] 64 alpha[92] 25 alpha[93] 36 alpha[94] 30 alpha[95] 50 alpha[96] 21 alpha[97] 31 alpha[98] 40 alpha[99] 21 alpha[100] 21 alpha[101] 33 alpha[102] 26 alpha[103] 380 alpha[104] 21 alpha[105] 32 alpha[106] 37 alpha[107] 200 alpha[108] 1200 alpha[109] 70 [ reached getOption("max.print") -- omitted 138 rows ] For each parameter, n.eff is a crude measure of effective sample size, and Rhat is the potential scale reduction factor (at convergence, Rhat=1). DIC info (using the rule, pD = Dbar-Dhat) pD = 238.6 and DIC = 11480.5 DIC is an estimate of expected predictive error (lower deviance is better). |
out5を分析してみる。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 |
> out5$mean $mu [1] 2.104949 $beta2 [1] -0.003049007 $alpha [1] -2.122921333 -2.354116000 0.359999101 -0.114509678 0.993117667 [6] -2.763880667 -1.290029767 0.611616167 -1.813718833 -0.348436322 [11] 1.260563100 1.452716000 0.646377700 -0.352707276 -0.531635158 [16] 0.415263840 0.313228281 0.609391867 1.478276000 0.520807090 [21] 0.239124742 -0.130443668 0.434675638 -2.674777333 0.668107400 [26] 0.080337891 0.851562133 1.541304333 -0.539186232 -1.846953133 [31] -0.534560880 1.175623733 2.080695000 -2.029831000 1.499397333 [36] 0.559953067 1.366510567 -2.563258000 0.467677858 0.987876533 [41] -0.127835027 -0.198349800 0.901481200 1.972063333 1.274677467 [46] -0.636459933 -3.085690333 1.160345633 1.060572167 0.904823700 [51] -1.341830567 0.720752433 0.557925233 0.364120982 0.812902167 [56] -1.360619867 1.601717667 1.011599367 0.999676567 -0.961164667 [61] 0.716875633 0.150129767 0.923923100 1.062304500 1.356106467 [66] -1.848001100 1.413582667 -1.394002833 0.546797307 -1.557273867 [71] -2.123988000 1.423280000 0.581043867 0.709653400 -1.618418467 [76] -0.890481933 0.615865167 -3.095572333 1.227935400 -0.013919375 [81] 0.689599533 -0.191344689 0.209833316 1.262264633 0.539892533 [86] 0.982224000 1.384211333 1.122848067 1.062521300 0.542594909 [91] -0.467184855 0.619482967 0.442449747 0.295036413 -0.536659847 [96] 1.486045333 0.689429433 0.078092412 1.557955000 0.989693000 [101] 0.362205116 1.025815333 -3.071142667 1.316964400 0.810614600 [106] 0.041368670 -2.408858667 -3.080385000 -0.412339308 1.261972733 [111] 0.468872127 1.392187000 0.682326000 0.080959131 -0.177613883 [116] 1.039769300 -1.335921600 0.044218231 0.300133776 0.580480943 [121] 0.871795200 -0.013783638 -1.929673000 -2.366847667 -3.080540333 [126] 0.746957800 0.460892530 -2.507114000 -0.247857756 0.105251678 [131] 0.350529558 -2.031433667 0.312466555 -0.826847733 -2.680587000 [136] 0.550041400 1.585201667 0.450249630 -0.408810217 0.377502775 [141] 0.863639767 1.030932000 -2.237260333 -2.858016000 0.435844813 [146] 1.084902933 0.185251457 0.037503798 1.249358233 -0.685159547 [151] 1.291263667 1.321194667 -0.082020850 -0.543770517 -0.158191753 [156] -0.067571764 -2.515288333 -1.070064067 0.851986567 -2.756776000 [161] 0.469352790 -1.148747867 0.448634590 1.149136133 0.767644133 [166] -1.242921133 -2.671537333 -1.769623100 -0.809407500 0.953503667 [171] -0.095610534 0.918416533 1.143135200 -1.627630167 0.407326688 [176] -0.542985517 -2.873948333 -2.399659667 0.461122077 -2.028432567 [181] -0.047778966 0.799079600 -1.506363633 -0.689382533 -0.008908012 [186] 0.041743421 1.315163100 1.137004467 1.237068433 0.038612900 [191] 1.187769200 0.586918110 1.307008667 -0.114804520 0.091091861 [196] 0.578139833 -1.561225533 1.516106333 -3.370123667 1.128425233 [201] 0.710318367 -1.854165967 0.695243067 -0.351683242 -2.509598667 [206] -0.069817385 1.147113967 0.484751017 0.852600733 -0.071053643 [211] 1.435690000 0.434538123 0.949748400 -1.844876800 0.419775840 [216] 0.991522333 0.828042733 1.142122533 0.559150200 1.042897567 [221] -0.959826400 -3.375218333 0.460715973 -1.189937233 1.450379000 [226] -0.715615907 -1.622942833 -2.510792333 0.708523933 1.235605700 [231] 1.659901000 1.566020333 1.574184000 1.259885433 1.490054000 $eps [1] -0.006911767 0.065316257 -0.166528909 -0.114507471 0.047833060 0.088227762 [7] 0.209970180 -0.168289142 -0.074628521 $sd.alpha [1] 1.328245 $sd.eps [1] 0.1587864 $deviance [1] 11241.87 |
mu + beta2 * first[i,j] + alpha[j] + eps[i]
mu 2.104949
beta2 -0.003049007
beta2は、ゼロに近いのであまり初観察者の影響はなさそう。
年のランダム効果epsは、
-0.006911767 0.065316257 -0.166528909 -0.114507471 0.047833060 0.088227762 0.209970180 -0.168289142 -0.074628521
|
1 2 3 4 5 6 7 8 9 10 |
> y1999_u <- out5$mean$mu + out5$mean$alpha + out5$mean$beta2*first[,1] + out5$mean$eps[1] > y2000_u <- out5$mean$mu + out5$mean$alpha + out5$mean$beta2*first[,2] + out5$mean$eps[2] > y2001_u <- out5$mean$mu + out5$mean$alpha + out5$mean$beta2*first[,3] + out5$mean$eps[3] > y2002_u <- out5$mean$mu + out5$mean$alpha + out5$mean$beta2*first[,4] + out5$mean$eps[4] > y2003_u <- out5$mean$mu + out5$mean$alpha + out5$mean$beta2*first[,5] + out5$mean$eps[5] > y2004_u <- out5$mean$mu + out5$mean$alpha + out5$mean$beta2*first[,6] + out5$mean$eps[6] > y2005_u <- out5$mean$mu + out5$mean$alpha + out5$mean$beta2*first[,7] + out5$mean$eps[7] > y2006_u <- out5$mean$mu + out5$mean$alpha + out5$mean$beta2*first[,8] + out5$mean$eps[8] > y2007_u <- out5$mean$mu + out5$mean$alpha + out5$mean$beta2*first[,9] + out5$mean$eps[9] > boxplot(exp(y1999_u), exp(y2000_u), exp(y2001_u), exp(y2002_u), exp(y2003_u), exp(y2004_u), exp(y2005_u), exp(y2006_u), exp(y2007_u), names=c(1999:2007)) |
念のため、各年における初観察者と経験者を分けて、ボックスプロットで表示してみる。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 |
> y2000_beg <- 0 > y2000_exp <- 0 > y2001_beg <- 0 > y2002_beg <- 0 > y2003_beg <- 0 > y2004_beg <- 0 > y2005_beg <- 0 > y2006_beg <- 0 > y2007_beg <- 0 > y2001_exp <- 0 > y2002_exp <- 0 > y2003_exp <- 0 > y2004_exp <- 0 > y2005_exp <- 0 > y2006_exp <- 0 > y2007_exp <- 0 > > for (i in 1:235) {if (first[,1][i] == 1 ) {y1999_beg[i]<- out5$mean$mu + out5$mean$alpha[i] + out5$mean$beta2*first[,1][i] + out5$mean$eps[1]} else {y1999_beg[i] <- NA}} > for (i in 1:235) {if (first[,1][i] == 1 ) {y2000_beg[i]<- out5$mean$mu + out5$mean$alpha[i] + out5$mean$beta2*first[,2][i] + out5$mean$eps[2]} else {y2000_beg[i] <- NA}} > for (i in 1:235) {if (first[,1][i] == 1 ) {y2000_beg[i]<- out5$mean$mu + out5$mean$alpha[i] + out5$mean$beta2*first[,2][i] + out5$mean$eps[2]} else {y2000_beg[i] <- NA}} > for (i in 1:235) {if (first[,1][i] == 1 ) {y2001_beg[i]<- out5$mean$mu + out5$mean$alpha[i] + out5$mean$beta2*first[,3][i] + out5$mean$eps[3]} else {y2001_beg[i] <- NA}} > for (i in 1:235) {if (first[,1][i] == 1 ) {y2002_beg[i]<- out5$mean$mu + out5$mean$alpha[i] + out5$mean$beta2*first[,4][i] + out5$mean$eps[3]} else {y2002_beg[i] <- NA}} > for (i in 1:235) {if (first[,1][i] == 1 ) {y2002_beg[i]<- out5$mean$mu + out5$mean$alpha[i] + out5$mean$beta2*first[,4][i] + out5$mean$eps[4]} else {y2002_beg[i] <- NA}} > for (i in 1:235) {if (first[,1][i] == 1 ) {y2003_beg[i]<- out5$mean$mu + out5$mean$alpha[i] + out5$mean$beta2*first[,5][i] + out5$mean$eps[5]} else {y2003_beg[i] <- NA}} > for (i in 1:235) {if (first[,1][i] == 1 ) {y2004_beg[i]<- out5$mean$mu + out5$mean$alpha[i] + out5$mean$beta2*first[,6][i] + out5$mean$eps[6]} else {y2004_beg[i] <- NA}} > for (i in 1:235) {if (first[,1][i] == 1 ) {y2005_beg[i]<- out5$mean$mu + out5$mean$alpha[i] + out5$mean$beta2*first[,7][i] + out5$mean$eps[7]} else {y2005_beg[i] <- NA}} > for (i in 1:235) {if (first[,1][i] == 1 ) {y2006_beg[i]<- out5$mean$mu + out5$mean$alpha[i] + out5$mean$beta2*first[,8][i] + out5$mean$eps[8]} else {y2006_beg[i] <- NA}} > for (i in 1:235) {if (first[,1][i] == 1 ) {y2007_beg[i]<- out5$mean$mu + out5$mean$alpha[i] + out5$mean$beta2*first[,9][i] + out5$mean$eps[9]} else {y2007_beg[i] <- NA}} > > for (i in 1:235) {if (first[,1][i] == 0 ) {y1999_exp[i]<- out5$mean$mu + out5$mean$alpha[i] + out5$mean$beta2*first[,1][i] + out5$mean$eps[1]} else {y1999_exp[i] <- NA}} > for (i in 1:235) {if (first[,1][i] == 1 ) {y2000_exp[i]<- out5$mean$mu + out5$mean$alpha[i] + out5$mean$beta2*first[,2][i] + out5$mean$eps[2]} else {y2000_exp[i] <- NA}} > for (i in 1:235) {if (first[,1][i] == 1 ) {y2001_exp[i]<- out5$mean$mu + out5$mean$alpha[i] + out5$mean$beta2*first[,3][i] + out5$mean$eps[3]} else {y2001_exp[i] <- NA}} > for (i in 1:235) {if (first[,1][i] == 1 ) {y2002_exp[i]<- out5$mean$mu + out5$mean$alpha[i] + out5$mean$beta2*first[,4][i] + out5$mean$eps[4]} else {y2002_exp[i] <- NA}} > for (i in 1:235) {if (first[,1][i] == 1 ) {y2003_exp[i]<- out5$mean$mu + out5$mean$alpha[i] + out5$mean$beta2*first[,5][i] + out5$mean$eps[5]} else {y2003_exp[i] <- NA}} > for (i in 1:235) {if (first[,1][i] == 1 ) {y2004_exp[i]<- out5$mean$mu + out5$mean$alpha[i] + out5$mean$beta2*first[,6][i] + out5$mean$eps[6]} else {y2004_exp[i] <- NA}} > for (i in 1:235) {if (first[,1][i] == 1 ) {y2005_exp[i]<- out5$mean$mu + out5$mean$alpha[i] + out5$mean$beta2*first[,7][i] + out5$mean$eps[7]} else {y2005_exp[i] <- NA}} > for (i in 1:235) {if (first[,1][i] == 1 ) {y2006_exp[i]<- out5$mean$mu + out5$mean$alpha[i] + out5$mean$beta2*first[,8][i] + out5$mean$eps[8]} else {y2006_exp[i] <- NA}} > for (i in 1:235) {if (first[,1][i] == 1 ) {y2007_exp[i]<- out5$mean$mu + out5$mean$alpha[i] + out5$mean$beta2*first[,9][i] + out5$mean$eps[9]} else {y2007_exp[i] <- NA}} > boxplot(exp(y1999_beg), exp(y1999_exp), exp(y2000_beg), exp(y2000_exp), exp(y2001_beg), exp(y2001_exp), exp(y2002_beg), exp(y2002_exp), exp(y2003_beg), exp(y2003_exp), exp(y2004_beg), exp(y2004_exp), exp(y2005_beg), exp(y2005_exp), exp(y2006_beg), exp(y2006_exp), exp(y2007_beg),exp(y2007_exp), names=c(1999,1999, 2000, 2000, 2001, 2001, 2002, 2002, 2003, 2003, 2004, 2004, 2005, 2005, 2006, 2006, 2007, 2007)) |
続いて、時間に伴う全般的な線形増減傾向を加える。モデルは、
mu + beta1 * year[i] + beta2 * first[i,j] + alpha[j] + eps[i]
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281 282 283 284 285 286 287 288 289 290 291 |
> # (g) Random site and random year effects, first-year fixed observer effect and overall linear time trend > # Specify model in BUGS language > sink("GLMM4.txt") > cat(" + model { + + # Priors + mu ~ dnorm(0, 0.01) # Overall intercept + beta1 ~ dnorm(0, 0.01) # Overall trend + beta2 ~ dnorm(0, 0.01) # First-year observer effect + + for (j in 1:nsite){ + alpha[j] ~ dnorm(0, tau.alpha) # Random site effects + } + tau.alpha <- 1/ (sd.alpha * sd.alpha) + sd.alpha ~ dunif(0, 5) + + for (i in 1:nyear){ + eps[i] ~ dnorm(0, tau.eps) # Random year effects + } + tau.eps <- 1/ (sd.eps * sd.eps) + sd.eps ~ dunif(0, 3) + + # Likelihood + for (i in 1:nyear){ + for (j in 1:nsite){ + C[i,j] ~ dpois(lambda[i,j]) + lambda[i,j] <- exp(log.lambda[i,j]) + log.lambda[i,j] <- mu + beta1 * year[i] + beta2 * first[i,j] + alpha[j] + eps[i] + } #j + } #i + } + ",fill = TRUE) > sink() > > # Bundle data > win.data <- list(C = t(C), nsite = nrow(C), nyear = ncol(C), first = t(first), year = ((1:9)-5) / 4) > > # Initial values > inits <- function() list(mu = runif(1, 0, 4), beta1 = runif(1, -1, 1), beta2 = runif(1, -1, 1), alpha = runif(235, -2, 2), eps = runif(9, -1, 1)) > > # Parameters monitored > params <- c("mu", "beta1", "beta2", "alpha", "eps", "sd.alpha", "sd.eps") > > # MCMC settings > ni <- 12000 > nt <- 6 > nb <- 6000 > nc <- 3 > > # Call WinBUGS from R (BRT 7 min) > out6 <- bugs(win.data, inits, params, "GLMM4.txt", n.chains = nc, + n.thin = nt, n.iter = ni, n.burnin = nb, debug = TRUE, bugs.directory = bugs.dir, working.directory = getwd()) > > # Summarize posteriors > print(out6, dig = 2) Inference for Bugs model at "GLMM4.txt", fit using WinBUGS, 3 chains, each with 12000 iterations (first 6000 discarded), n.thin = 6 n.sims = 3000 iterations saved mean sd 2.5% 25% 50% 75% 97.5% Rhat mu 2.09 0.11 1.90 2.00 2.08 2.15 2.34 1.19 beta1 -0.01 0.10 -0.21 -0.07 -0.01 0.05 0.19 1.01 beta2 0.00 0.02 -0.04 -0.02 0.00 0.01 0.04 1.00 alpha[1] -2.12 0.34 -2.81 -2.35 -2.10 -1.88 -1.50 1.01 alpha[2] -2.36 0.37 -3.12 -2.60 -2.34 -2.10 -1.69 1.00 alpha[3] 0.37 0.14 0.09 0.27 0.37 0.46 0.63 1.06 alpha[4] -0.11 0.15 -0.42 -0.21 -0.10 0.00 0.18 1.03 alpha[5] 1.00 0.12 0.75 0.92 1.00 1.08 1.22 1.06 alpha[6] -2.76 0.48 -3.78 -3.06 -2.72 -2.43 -1.92 1.01 alpha[7] -1.29 0.26 -1.82 -1.46 -1.28 -1.10 -0.79 1.01 alpha[8] 0.61 0.13 0.36 0.53 0.62 0.70 0.85 1.05 alpha[9] -1.81 0.32 -2.46 -2.01 -1.79 -1.59 -1.21 1.01 alpha[10] -0.34 0.17 -0.69 -0.46 -0.34 -0.23 -0.01 1.03 alpha[11] 1.27 0.11 1.03 1.19 1.27 1.34 1.48 1.07 alpha[12] 1.46 0.11 1.23 1.38 1.46 1.53 1.67 1.07 alpha[13] 0.65 0.13 0.39 0.57 0.65 0.74 0.89 1.04 alpha[14] -0.35 0.17 -0.69 -0.46 -0.34 -0.23 -0.02 1.02 alpha[15] -0.53 0.19 -0.90 -0.65 -0.53 -0.40 -0.18 1.02 alpha[16] 0.42 0.13 0.16 0.33 0.42 0.51 0.67 1.05 alpha[17] 0.32 0.13 0.05 0.23 0.32 0.41 0.59 1.04 alpha[18] 0.61 0.13 0.35 0.53 0.62 0.70 0.85 1.06 alpha[19] 1.48 0.11 1.25 1.41 1.49 1.56 1.69 1.07 alpha[20] 0.52 0.13 0.25 0.44 0.53 0.61 0.76 1.05 alpha[21] 0.25 0.14 -0.04 0.15 0.25 0.34 0.50 1.03 alpha[22] -0.12 0.16 -0.45 -0.23 -0.12 -0.01 0.18 1.02 alpha[23] 0.44 0.13 0.17 0.35 0.44 0.53 0.69 1.04 alpha[24] -2.66 0.42 -3.55 -2.93 -2.63 -2.36 -1.91 1.00 alpha[25] 0.67 0.13 0.41 0.59 0.68 0.76 0.92 1.06 alpha[26] 0.08 0.15 -0.22 -0.01 0.09 0.19 0.36 1.04 alpha[27] 0.86 0.12 0.61 0.78 0.87 0.94 1.09 1.05 alpha[28] 1.55 0.11 1.32 1.48 1.55 1.62 1.75 1.08 alpha[29] -0.53 0.18 -0.89 -0.65 -0.53 -0.41 -0.18 1.02 alpha[30] -1.84 0.30 -2.47 -2.03 -1.83 -1.63 -1.28 1.01 alpha[31] -0.53 0.18 -0.87 -0.65 -0.52 -0.41 -0.20 1.03 alpha[32] 1.18 0.11 0.95 1.11 1.19 1.26 1.40 1.06 alpha[33] 2.09 0.10 1.87 2.02 2.09 2.16 2.28 1.08 alpha[34] -2.03 0.36 -2.76 -2.27 -2.01 -1.78 -1.38 1.00 alpha[35] 1.51 0.11 1.29 1.43 1.51 1.58 1.71 1.06 alpha[36] 0.57 0.13 0.31 0.48 0.57 0.66 0.83 1.05 alpha[37] 1.37 0.11 1.14 1.30 1.38 1.45 1.58 1.06 alpha[38] -2.56 0.43 -3.44 -2.83 -2.55 -2.26 -1.80 1.01 alpha[39] 0.47 0.13 0.20 0.39 0.47 0.56 0.73 1.05 alpha[40] 0.99 0.12 0.75 0.91 0.99 1.07 1.22 1.05 alpha[41] -0.12 0.16 -0.45 -0.23 -0.12 -0.02 0.18 1.03 alpha[42] -0.19 0.17 -0.54 -0.30 -0.19 -0.08 0.12 1.02 alpha[43] 0.90 0.12 0.66 0.83 0.91 0.99 1.12 1.06 alpha[44] 1.98 0.10 1.77 1.91 1.98 2.05 2.17 1.09 alpha[45] 1.28 0.11 1.04 1.21 1.28 1.36 1.50 1.06 alpha[46] -0.63 0.18 -0.99 -0.75 -0.63 -0.51 -0.28 1.02 alpha[47] -3.08 0.51 -4.21 -3.39 -3.06 -2.71 -2.19 1.00 alpha[48] 1.16 0.12 0.92 1.09 1.17 1.24 1.38 1.06 alpha[49] 1.07 0.12 0.83 0.99 1.07 1.15 1.28 1.06 alpha[50] 0.91 0.12 0.66 0.83 0.91 0.99 1.13 1.07 alpha[51] -1.33 0.24 -1.81 -1.49 -1.33 -1.17 -0.89 1.01 alpha[52] 0.72 0.12 0.47 0.65 0.73 0.81 0.96 1.06 alpha[53] 0.56 0.13 0.31 0.48 0.57 0.65 0.80 1.06 alpha[54] 0.37 0.14 0.10 0.28 0.37 0.46 0.62 1.04 alpha[55] 0.82 0.12 0.57 0.74 0.82 0.91 1.05 1.05 alpha[56] -1.36 0.26 -1.89 -1.53 -1.34 -1.18 -0.88 1.01 alpha[57] 1.61 0.11 1.38 1.54 1.61 1.68 1.80 1.08 alpha[58] 1.02 0.12 0.78 0.94 1.02 1.10 1.23 1.06 alpha[59] 1.00 0.12 0.76 0.93 1.01 1.08 1.23 1.05 alpha[60] -0.94 0.22 -1.39 -1.09 -0.94 -0.79 -0.52 1.02 alpha[61] 0.72 0.13 0.47 0.64 0.72 0.81 0.97 1.06 alpha[62] 0.16 0.14 -0.12 0.06 0.16 0.25 0.44 1.05 alpha[63] 0.93 0.12 0.68 0.85 0.93 1.01 1.15 1.06 alpha[64] 1.07 0.12 0.83 0.99 1.07 1.15 1.29 1.06 alpha[65] 1.36 0.11 1.13 1.29 1.37 1.44 1.58 1.06 alpha[66] -1.85 0.30 -2.47 -2.04 -1.83 -1.64 -1.29 1.01 alpha[67] 1.42 0.11 1.19 1.34 1.43 1.50 1.63 1.06 alpha[68] -1.38 0.26 -1.92 -1.55 -1.38 -1.20 -0.90 1.01 alpha[69] 0.56 0.13 0.29 0.47 0.56 0.64 0.81 1.04 alpha[70] -1.55 0.26 -2.09 -1.72 -1.54 -1.37 -1.03 1.01 alpha[71] -2.13 0.34 -2.82 -2.35 -2.12 -1.89 -1.51 1.00 alpha[72] 1.43 0.11 1.20 1.36 1.44 1.50 1.63 1.07 alpha[73] 0.58 0.13 0.32 0.50 0.59 0.67 0.83 1.05 alpha[74] 0.71 0.12 0.47 0.63 0.72 0.80 0.95 1.05 alpha[75] -1.62 0.28 -2.18 -1.80 -1.61 -1.42 -1.10 1.00 alpha[76] -0.89 0.20 -1.31 -1.02 -0.88 -0.75 -0.51 1.02 alpha[77] 0.62 0.13 0.37 0.54 0.63 0.71 0.87 1.05 alpha[78] -3.08 0.50 -4.16 -3.39 -3.04 -2.73 -2.22 1.00 alpha[79] 1.23 0.12 1.00 1.16 1.24 1.31 1.46 1.06 alpha[80] 0.00 0.15 -0.30 -0.10 0.00 0.10 0.28 1.04 alpha[81] 0.69 0.13 0.42 0.60 0.70 0.78 0.94 1.04 alpha[82] -0.18 0.16 -0.50 -0.29 -0.18 -0.07 0.13 1.03 alpha[83] 0.21 0.14 -0.08 0.12 0.22 0.31 0.49 1.04 alpha[84] 1.26 0.12 1.03 1.19 1.27 1.34 1.48 1.06 alpha[85] 0.55 0.13 0.28 0.46 0.55 0.64 0.79 1.06 alpha[86] 0.99 0.12 0.75 0.91 0.99 1.07 1.21 1.06 alpha[87] 1.39 0.11 1.16 1.31 1.39 1.47 1.60 1.07 alpha[88] 1.13 0.12 0.90 1.05 1.13 1.21 1.35 1.07 alpha[89] 1.06 0.12 0.82 0.99 1.07 1.15 1.29 1.06 alpha[90] 0.55 0.13 0.29 0.46 0.55 0.64 0.79 1.05 alpha[91] -0.46 0.17 -0.81 -0.58 -0.46 -0.34 -0.14 1.02 alpha[92] 0.62 0.13 0.35 0.54 0.63 0.70 0.85 1.06 alpha[93] 0.45 0.13 0.18 0.36 0.45 0.54 0.71 1.03 alpha[94] 0.30 0.14 0.02 0.21 0.31 0.40 0.57 1.05 alpha[95] -0.54 0.18 -0.89 -0.65 -0.53 -0.42 -0.21 1.03 alpha[96] 1.49 0.11 1.27 1.42 1.50 1.57 1.70 1.07 alpha[97] 0.69 0.13 0.43 0.61 0.70 0.78 0.94 1.05 alpha[98] 0.08 0.15 -0.21 -0.01 0.09 0.18 0.36 1.04 alpha[99] 1.56 0.11 1.34 1.49 1.57 1.64 1.77 1.07 alpha[100] 0.99 0.12 0.74 0.92 1.00 1.08 1.21 1.08 alpha[101] 0.37 0.13 0.10 0.28 0.37 0.46 0.62 1.04 alpha[102] 1.03 0.12 0.79 0.95 1.03 1.11 1.25 1.06 alpha[103] -3.07 0.51 -4.16 -3.37 -3.03 -2.71 -2.17 1.00 alpha[104] 1.32 0.11 1.09 1.25 1.33 1.40 1.53 1.06 alpha[105] 0.82 0.13 0.57 0.74 0.82 0.90 1.07 1.07 alpha[106] 0.04 0.15 -0.26 -0.05 0.05 0.14 0.32 1.04 alpha[107] -2.40 0.40 -3.23 -2.65 -2.38 -2.12 -1.68 1.00 alpha[108] -3.07 0.51 -4.13 -3.41 -3.03 -2.71 -2.16 1.00 n.eff mu 16 beta1 3000 beta2 3000 alpha[1] 400 alpha[2] 530 alpha[3] 39 alpha[4] 65 alpha[5] 41 alpha[6] 390 alpha[7] 180 alpha[8] 48 alpha[9] 300 alpha[10] 62 alpha[11] 37 alpha[12] 35 alpha[13] 55 alpha[14] 87 alpha[15] 110 alpha[16] 42 alpha[17] 60 alpha[18] 41 alpha[19] 36 alpha[20] 57 alpha[21] 65 alpha[22] 98 alpha[23] 59 alpha[24] 630 alpha[25] 45 alpha[26] 55 alpha[27] 53 alpha[28] 32 alpha[29] 100 alpha[30] 190 alpha[31] 81 alpha[32] 39 alpha[33] 32 alpha[34] 930 alpha[35] 40 alpha[36] 50 alpha[37] 40 alpha[38] 370 alpha[39] 47 alpha[40] 43 alpha[41] 72 alpha[42] 100 alpha[43] 41 alpha[44] 29 alpha[45] 38 alpha[46] 89 alpha[47] 1400 alpha[48] 40 alpha[49] 39 alpha[50] 33 alpha[51] 250 alpha[52] 40 alpha[53] 43 alpha[54] 50 alpha[55] 48 alpha[56] 260 alpha[57] 31 alpha[58] 38 alpha[59] 45 alpha[60] 120 alpha[61] 40 alpha[62] 43 alpha[63] 40 alpha[64] 42 alpha[65] 41 alpha[66] 220 alpha[67] 38 alpha[68] 340 alpha[69] 60 alpha[70] 290 alpha[71] 470 alpha[72] 34 alpha[73] 48 alpha[74] 48 alpha[75] 530 alpha[76] 110 alpha[77] 49 alpha[78] 830 alpha[79] 37 alpha[80] 54 alpha[81] 62 alpha[82] 80 alpha[83] 53 alpha[84] 40 alpha[85] 44 alpha[86] 41 alpha[87] 37 alpha[88] 37 alpha[89] 41 alpha[90] 50 alpha[91] 110 alpha[92] 42 alpha[93] 72 alpha[94] 47 alpha[95] 76 alpha[96] 33 alpha[97] 49 alpha[98] 62 alpha[99] 36 alpha[100] 30 alpha[101] 53 alpha[102] 42 alpha[103] 830 alpha[104] 40 alpha[105] 34 alpha[106] 51 alpha[107] 1400 alpha[108] 1100 [ reached getOption("max.print") -- omitted 139 rows ] For each parameter, n.eff is a crude measure of effective sample size, and Rhat is the potential scale reduction factor (at convergence, Rhat=1). DIC info (using the rule, pD = Dbar-Dhat) pD = 238.2 and DIC = 11479.8 DIC is an estimate of expected predictive error (lower deviance is better). |
out6を分析してみる。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 |
> out6$mean $mu [1] 2.085063 $beta1 [1] -0.009154471 $beta2 [1] -0.002999401 $alpha [1] -2.121660333 -2.359001667 0.365836564 -0.108265085 0.996244633 [6] -2.758898667 -1.285145200 0.614000433 -1.807261500 -0.344473649 [11] 1.267055267 1.457143667 0.650201500 -0.347992373 -0.530127205 [16] 0.419342477 0.321173905 0.614440033 1.482984333 0.524158783 [21] 0.245375930 -0.124918867 0.436854190 -2.658428333 0.674508433 [26] 0.084241284 0.860982567 1.548356333 -0.530089815 -1.837932100 [31] -0.528526949 1.182271567 2.086269000 -2.027974933 1.506314667 [36] 0.571134933 1.370145033 -2.563980333 0.472077600 0.992356200 [41] -0.123191919 -0.189657797 0.904876900 1.977820000 1.282166767 [46] -0.630209257 -3.083541000 1.163151200 1.066627533 0.906343400 [51] -1.333337867 0.724514700 0.563493510 0.366362733 0.822781167 [56] -1.356479633 1.606529000 1.016872100 1.004211467 -0.943225200 [61] 0.722553167 0.156437603 0.927923000 1.065279833 1.361183967 [66] -1.845652067 1.419557667 -1.383799233 0.555322733 -1.550089000 [71] -2.126376000 1.429583000 0.583130433 0.713956167 -1.616091900 [76] -0.887511567 0.624876367 -3.077685333 1.232039067 -0.003809320 [81] 0.691905133 -0.181689665 0.214050704 1.264761767 0.547119563 [86] 0.987865667 1.388491067 1.128587233 1.064622467 0.549873270 [91] -0.464682343 0.621395400 0.450293257 0.304084841 -0.535066743 [96] 1.493977000 0.694206433 0.080910404 1.563179000 0.994820367 [101] 0.367216832 1.031156467 -3.067826667 1.322167867 0.818755233 [106] 0.042176035 -2.399696667 -3.069789333 -0.405262311 1.271720067 [111] 0.473704973 1.396638867 0.687735533 0.080989330 -0.170121417 [116] 1.045320600 -1.339390400 0.044732159 0.305835518 0.587065813 [121] 0.874320100 -0.003812988 -1.925364733 -2.370491333 -3.067246000 [126] 0.750473733 0.467905303 -2.499054667 -0.233837003 0.112767731 [131] 0.357095846 -2.016635000 0.319667812 -0.823074153 -2.654804667 [136] 0.554863800 1.588065000 0.455359746 -0.397939218 0.386651698 [141] 0.868862767 1.036554067 -2.243072667 -2.849569333 0.441442890 [146] 1.088386333 0.191062960 0.046352361 1.253469500 -0.682729723 [151] 1.295975267 1.325780367 -0.079068819 -0.530122938 -0.151977748 [156] -0.062423352 -2.507417000 -1.060255233 0.856054033 -2.759573333 [161] 0.473516725 -1.154420733 0.454042444 1.156685400 0.770636867 [166] -1.237320500 -2.669161333 -1.760001800 -0.792575900 0.959639100 [171] -0.091621349 0.926969800 1.146099733 -1.621911567 0.414219153 [176] -0.541727069 -2.867360000 -2.384033667 0.463937447 -2.021987567 [181] -0.040925334 0.804279700 -1.503639700 -0.680473200 -0.005774659 [186] 0.045866085 1.320252533 1.141527467 1.242887433 0.046477648 [191] 1.192837767 0.592775367 1.312483833 -0.104666120 0.093228177 [196] 0.581613537 -1.552603000 1.524025333 -3.368269667 1.133428233 [201] 0.714023000 -1.840431700 0.699158100 -0.341931412 -2.502227000 [206] -0.058752814 1.149989767 0.491406772 0.855939500 -0.073702302 [211] 1.442676000 0.437687986 0.955842200 -1.835774333 0.425450403 [216] 0.996394400 0.833488467 1.145997433 0.562134973 1.047379867 [221] -0.956829067 -3.373243667 0.465453783 -1.188607200 1.455708667 [226] -0.708938333 -1.613921200 -2.504643000 0.714282100 1.241204300 [231] 1.663679000 1.570201000 1.580968667 1.263252433 1.493981667 $eps [1] -0.001419146 0.073006750 -0.156694476 -0.103126514 0.062377340 0.105235248 [7] 0.229295271 -0.147793252 -0.051034461 $sd.alpha [1] 1.328803 $sd.eps [1] 0.1715431 $deviance [1] 11241.62 |
モデルは、mu + beta1 * year[i] + beta2 * first[i,j] + alpha[j] + eps[i]
$mu 2.085063
beta1 -0.009154471
beta2 -0.002999401
eps -0.001419146 0.073006750 -0.156694476 -0.103126514 0.062377340 0.105235248 0.229295271 -0.147793252 -0.051034461
注意はyear[]
|
1 2 3 |
> year = ((1:9)-5/4) > year [1] -0.25 0.75 1.75 2.75 3.75 4.75 5.75 6.75 7.75 |
|
1 2 3 4 5 6 7 8 9 10 |
> y1999_v <- out6$mean$mu + out6$mean$beta1*year[1] + out6$mean$beta2*first[,1] + out6$mean$alpha + out6$mean$eps[1] > y2000_v <- out6$mean$mu + out6$mean$beta1*year[2] + out6$mean$beta2*first[,2] + out6$mean$alpha + out6$mean$eps[2] > y2001_v <- out6$mean$mu + out6$mean$beta1*year[3] + out6$mean$beta2*first[,3] + out6$mean$alpha + out6$mean$eps[3] > y2002_v <- out6$mean$mu + out6$mean$beta1*year[4] + out6$mean$beta2*first[,4] + out6$mean$alpha + out6$mean$eps[4] > y2003_v <- out6$mean$mu + out6$mean$beta1*year[5] + out6$mean$beta2*first[,5] + out6$mean$alpha + out6$mean$eps[5] > y2004_v <- out6$mean$mu + out6$mean$beta1*year[6] + out6$mean$beta2*first[,6] + out6$mean$alpha + out6$mean$eps[6] > y2005_v <- out6$mean$mu + out6$mean$beta1*year[7] + out6$mean$beta2*first[,7] + out6$mean$alpha + out6$mean$eps[7] > y2006_v <- out6$mean$mu + out6$mean$beta1*year[8] + out6$mean$beta2*first[,8] + out6$mean$alpha + out6$mean$eps[8] > y2007_v <- out6$mean$mu + out6$mean$beta1*year[9] + out6$mean$beta2*first[,9] + out6$mean$alpha + out6$mean$eps[9] > boxplot(exp(y1999_v), exp(y2000_v), exp(y2001_v), exp(y2002_v), exp(y2003_v), exp(y2004_v), exp(y2005_v), exp(y2006_v), exp(y2007_v), names=c(1999:2007)) |
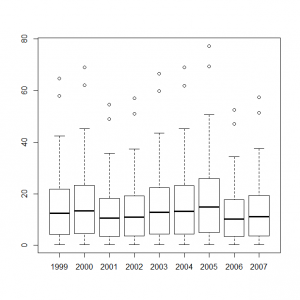
以下、前前々回の線形増減傾向を含まない場合と比較してみる。
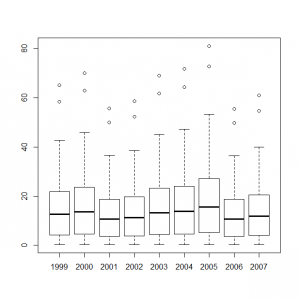
線形増減傾向はbeta2=-0.002999401と小さいので、ほとんどプロットには影響しなかった。
最後にフルモデル
mu + beta1 * year[i] + beta2 * first[i,j] + alpha[j] + gamma[newobs[i,j]] + eps[i]
ランダム観察者効果として
|
1 2 3 4 5 |
for (k in 1:nobs){ gamma[k] ~ dnorm(0, tau.gamma) # Random observer effects } tau.gamma <- 1/ (sd.gamma * sd.gamma) sd.gamma ~ dunif(0, 1) |
が含まれている。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281 282 283 284 285 286 287 288 289 290 291 292 293 294 295 296 297 |
> # (h) The full model > # Specify model in BUGS language > sink("GLMM5.txt") > cat(" + model { + + # Priors + mu ~ dnorm(0, 0.01) # Overall intercept + beta1 ~ dnorm(0, 0.01) # Overall trend + beta2 ~ dnorm(0, 0.01) # First-year observer effect + + for (j in 1:nsite){ + alpha[j] ~ dnorm(0, tau.alpha) # Random site effects + } + tau.alpha <- 1/ (sd.alpha * sd.alpha) + sd.alpha ~ dunif(0, 3) + + for (i in 1:nyear){ + eps[i] ~ dnorm(0, tau.eps) # Random year effects + } + tau.eps <- 1/ (sd.eps * sd.eps) + sd.eps ~ dunif(0, 1) + + for (k in 1:nobs){ + gamma[k] ~ dnorm(0, tau.gamma) # Random observer effects + } + tau.gamma <- 1/ (sd.gamma * sd.gamma) + sd.gamma ~ dunif(0, 1) + + # Likelihood + for (i in 1:nyear){ + for (j in 1:nsite){ + C[i,j] ~ dpois(lambda[i,j]) + lambda[i,j] <- exp(log.lambda[i,j]) + log.lambda[i,j] <- mu + beta1 * year[i] + beta2 * first[i,j] + alpha[j] + gamma[newobs[i,j]] + eps[i] + } #j + } #i + } + ",fill = TRUE) > sink() > > # Bundle data > win.data <- list(C = t(C), nsite = nrow(C), nyear = ncol(C), nobs = 272, newobs = t(newobs), first = t(first), year = ((1:9)-5) / 4) > > # Initial values > inits <- function() list(mu = runif(1, 0, 4), beta1 = runif(1, -1, 1), beta2 = runif(1, -1, 1), alpha = runif(235, -1, 1), gamma = runif(272, -1, 1), eps = runif(9, -1, 1)) > > # Parameters monitored > params <- c("mu", "beta1", "beta2", "alpha", "gamma", "eps", "sd.alpha", "sd.gamma", "sd.eps") > > # MCMC settings > ni <- 12000 > nt <- 6 > nb <- 6000 > nc <- 3 > > # Call WinBUGS from R (BRT 11 min) > out7 <- bugs(win.data, inits, params, "GLMM5.txt", n.chains = nc, + n.thin = nt, n.iter = ni, n.burnin = nb, debug = TRUE, bugs.directory = bugs.dir, working.directory = getwd()) > > # Summarize posteriors > print(out7, dig = 2) Inference for Bugs model at "GLMM5.txt", fit using WinBUGS, 3 chains, each with 12000 iterations (first 6000 discarded), n.thin = 6 n.sims = 3000 iterations saved mean sd 2.5% 25% 50% 75% 97.5% Rhat mu 2.08 0.11 1.89 2.00 2.08 2.16 2.29 1.06 beta1 -0.02 0.10 -0.31 -0.06 -0.01 0.04 0.15 1.16 beta2 0.02 0.02 -0.02 0.01 0.02 0.04 0.06 1.00 alpha[1] -2.44 0.36 -3.21 -2.68 -2.43 -2.19 -1.75 1.01 alpha[2] -2.10 0.40 -2.94 -2.37 -2.09 -1.83 -1.37 1.00 alpha[3] 0.37 0.25 -0.13 0.20 0.37 0.53 0.86 1.01 alpha[4] -0.46 0.20 -0.85 -0.60 -0.46 -0.33 -0.08 1.02 alpha[5] 0.93 0.33 0.30 0.70 0.92 1.16 1.58 1.01 alpha[6] -2.72 0.49 -3.74 -3.03 -2.70 -2.38 -1.78 1.00 alpha[7] -1.24 0.28 -1.81 -1.43 -1.23 -1.05 -0.72 1.02 alpha[8] 0.76 0.24 0.28 0.60 0.76 0.92 1.23 1.02 alpha[9] -1.79 0.33 -2.45 -2.01 -1.78 -1.57 -1.16 1.01 alpha[10] -0.44 0.20 -0.85 -0.58 -0.44 -0.30 -0.07 1.02 alpha[11] 1.01 0.19 0.64 0.88 1.01 1.15 1.38 1.03 alpha[12] 1.21 0.22 0.79 1.07 1.21 1.36 1.64 1.01 alpha[13] 0.60 0.36 -0.11 0.35 0.60 0.85 1.29 1.01 alpha[14] -0.17 0.25 -0.66 -0.34 -0.17 0.00 0.30 1.00 alpha[15] -0.60 0.24 -1.09 -0.76 -0.60 -0.44 -0.14 1.01 alpha[16] 0.38 0.35 -0.30 0.16 0.38 0.61 1.05 1.01 alpha[17] 0.19 0.19 -0.19 0.07 0.19 0.31 0.55 1.01 alpha[18] 0.60 0.34 -0.08 0.38 0.60 0.83 1.25 1.02 alpha[19] 1.41 0.16 1.11 1.31 1.42 1.51 1.73 1.03 alpha[20] 0.47 0.36 -0.22 0.23 0.47 0.71 1.17 1.01 alpha[21] 0.25 0.28 -0.30 0.06 0.25 0.44 0.78 1.00 alpha[22] -0.33 0.19 -0.73 -0.46 -0.32 -0.19 0.04 1.03 alpha[23] 0.36 0.24 -0.10 0.20 0.37 0.52 0.83 1.01 alpha[24] -2.50 0.52 -3.55 -2.84 -2.48 -2.15 -1.54 1.00 alpha[25] 0.59 0.19 0.20 0.46 0.59 0.72 0.97 1.02 alpha[26] 0.08 0.34 -0.61 -0.15 0.08 0.31 0.75 1.00 alpha[27] 0.78 0.18 0.43 0.65 0.79 0.91 1.14 1.03 alpha[28] 1.41 0.16 1.08 1.30 1.41 1.52 1.72 1.03 alpha[29] -0.63 0.23 -1.07 -0.78 -0.63 -0.47 -0.19 1.01 alpha[30] -1.85 0.43 -2.70 -2.14 -1.85 -1.55 -1.02 1.01 alpha[31] -0.46 0.26 -1.00 -0.64 -0.46 -0.29 0.04 1.01 alpha[32] 1.13 0.14 0.86 1.03 1.13 1.23 1.41 1.03 alpha[33] 1.85 0.17 1.52 1.73 1.84 1.96 2.18 1.02 alpha[34] -2.15 0.36 -2.88 -2.38 -2.14 -1.90 -1.46 1.00 alpha[35] 1.26 0.16 0.94 1.16 1.26 1.37 1.56 1.04 alpha[36] 0.86 0.21 0.44 0.72 0.86 1.01 1.27 1.01 alpha[37] 1.37 0.34 0.71 1.14 1.36 1.59 2.06 1.02 alpha[38] -2.57 0.46 -3.52 -2.89 -2.55 -2.25 -1.73 1.00 alpha[39] 0.30 0.28 -0.25 0.12 0.30 0.48 0.87 1.02 alpha[40] 0.92 0.33 0.26 0.71 0.93 1.14 1.56 1.00 alpha[41] -0.44 0.28 -0.98 -0.63 -0.44 -0.26 0.12 1.01 alpha[42] -0.30 0.18 -0.66 -0.42 -0.30 -0.18 0.06 1.01 alpha[43] 1.16 0.19 0.80 1.03 1.17 1.30 1.51 1.01 alpha[44] 1.70 0.17 1.38 1.59 1.70 1.81 2.02 1.02 alpha[45] 1.21 0.35 0.50 0.99 1.22 1.45 1.86 1.02 alpha[46] -0.54 0.28 -1.11 -0.74 -0.55 -0.35 0.00 1.01 alpha[47] -2.84 0.52 -3.94 -3.18 -2.80 -2.46 -1.93 1.00 alpha[48] 1.12 0.17 0.80 1.01 1.12 1.24 1.46 1.02 alpha[49] 0.84 0.17 0.50 0.73 0.85 0.96 1.17 1.03 alpha[50] 0.83 0.35 0.15 0.60 0.84 1.06 1.51 1.00 alpha[51] -1.47 0.30 -2.09 -1.67 -1.47 -1.26 -0.91 1.01 alpha[52] 0.70 0.34 -0.01 0.48 0.70 0.92 1.38 1.02 alpha[53] 0.52 0.35 -0.19 0.29 0.52 0.76 1.17 1.01 alpha[54] 0.11 0.18 -0.26 -0.01 0.11 0.23 0.45 1.01 alpha[55] 0.74 0.19 0.36 0.62 0.75 0.87 1.09 1.03 alpha[56] -1.36 0.27 -1.89 -1.54 -1.36 -1.18 -0.85 1.01 alpha[57] 1.87 0.18 1.52 1.74 1.86 1.99 2.22 1.02 alpha[58] 1.30 0.20 0.92 1.17 1.31 1.44 1.69 1.01 alpha[59] 1.00 0.35 0.31 0.76 1.00 1.24 1.67 1.00 alpha[60] -0.95 0.37 -1.68 -1.20 -0.95 -0.71 -0.22 1.01 alpha[61] 0.54 0.15 0.25 0.44 0.54 0.65 0.81 1.02 alpha[62] 0.09 0.18 -0.26 -0.03 0.10 0.23 0.45 1.02 alpha[63] 0.60 0.28 0.06 0.40 0.60 0.78 1.15 1.01 alpha[64] 1.06 0.25 0.59 0.89 1.06 1.23 1.56 1.02 alpha[65] 1.62 0.18 1.27 1.49 1.62 1.75 1.97 1.01 alpha[66] -1.59 0.34 -2.27 -1.82 -1.58 -1.36 -0.94 1.00 alpha[67] 1.15 0.13 0.90 1.06 1.15 1.25 1.41 1.03 alpha[68] -1.30 0.40 -2.11 -1.56 -1.30 -1.03 -0.50 1.01 alpha[69] 0.50 0.18 0.14 0.39 0.50 0.63 0.85 1.03 alpha[70] -1.60 0.36 -2.33 -1.84 -1.59 -1.36 -0.90 1.01 alpha[71] -2.08 0.39 -2.88 -2.34 -2.06 -1.82 -1.37 1.01 alpha[72] 1.12 0.27 0.59 0.94 1.12 1.30 1.64 1.02 alpha[73] 0.54 0.35 -0.15 0.32 0.55 0.77 1.24 1.01 alpha[74] 0.54 0.17 0.20 0.43 0.54 0.66 0.87 1.03 alpha[75] -1.53 0.41 -2.35 -1.81 -1.52 -1.25 -0.76 1.00 alpha[76] -0.63 0.25 -1.12 -0.80 -0.63 -0.46 -0.17 1.01 alpha[77] 0.88 0.19 0.52 0.74 0.88 1.01 1.25 1.02 alpha[78] -2.84 0.53 -3.94 -3.18 -2.81 -2.46 -1.89 1.00 alpha[79] 1.08 0.13 0.83 0.99 1.07 1.17 1.33 1.04 alpha[80] -0.04 0.18 -0.38 -0.16 -0.04 0.08 0.30 1.01 alpha[81] 0.63 0.35 -0.03 0.39 0.63 0.86 1.35 1.01 alpha[82] -0.44 0.30 -1.06 -0.64 -0.44 -0.24 0.13 1.01 alpha[83] 0.50 0.21 0.08 0.36 0.50 0.65 0.91 1.01 alpha[84] 1.16 0.34 0.48 0.94 1.15 1.38 1.83 1.00 alpha[85] 0.81 0.19 0.44 0.67 0.81 0.95 1.16 1.01 alpha[86] 0.94 0.14 0.68 0.85 0.94 1.04 1.21 1.02 alpha[87] 1.00 0.18 0.66 0.88 0.99 1.12 1.34 1.01 alpha[88] 1.13 0.33 0.49 0.92 1.13 1.35 1.78 1.01 alpha[89] 0.92 0.14 0.66 0.83 0.92 1.02 1.19 1.03 alpha[90] 0.51 0.34 -0.18 0.28 0.51 0.75 1.17 1.01 alpha[91] -0.44 0.36 -1.14 -0.68 -0.44 -0.19 0.25 1.01 alpha[92] 0.58 0.36 -0.11 0.34 0.58 0.83 1.30 1.00 alpha[93] 0.70 0.19 0.33 0.57 0.70 0.84 1.08 1.01 alpha[94] 0.29 0.35 -0.42 0.06 0.29 0.52 0.96 1.02 alpha[95] -0.67 0.27 -1.21 -0.86 -0.67 -0.49 -0.15 1.01 alpha[96] 1.33 0.13 1.08 1.24 1.33 1.43 1.59 1.03 alpha[97] 0.65 0.35 -0.02 0.41 0.65 0.88 1.32 1.01 alpha[98] 0.07 0.35 -0.63 -0.16 0.08 0.30 0.72 1.00 alpha[99] 1.44 0.34 0.76 1.21 1.46 1.68 2.11 1.00 alpha[100] 0.81 0.13 0.56 0.72 0.81 0.90 1.07 1.04 alpha[101] 0.18 0.17 -0.14 0.06 0.19 0.30 0.52 1.01 alpha[102] 1.04 0.16 0.71 0.93 1.03 1.15 1.35 1.02 alpha[103] -2.91 0.58 -4.17 -3.28 -2.89 -2.51 -1.83 1.00 alpha[104] 1.27 0.26 0.75 1.09 1.27 1.45 1.79 1.01 alpha[105] 0.60 0.20 0.22 0.47 0.60 0.73 1.00 1.01 alpha[106] 0.03 0.20 -0.36 -0.10 0.03 0.16 0.42 1.01 alpha[107] -2.30 0.46 -3.23 -2.60 -2.29 -2.00 -1.44 1.00 alpha[108] -2.85 0.54 -3.99 -3.19 -2.83 -2.48 -1.89 1.00 n.eff mu 42 beta1 31 beta2 3000 alpha[1] 200 alpha[2] 2300 alpha[3] 220 alpha[4] 110 alpha[5] 200 alpha[6] 1200 alpha[7] 130 alpha[8] 130 alpha[9] 370 alpha[10] 98 alpha[11] 71 alpha[12] 340 alpha[13] 350 alpha[14] 610 alpha[15] 190 alpha[16] 290 alpha[17] 270 alpha[18] 98 alpha[19] 72 alpha[20] 330 alpha[21] 530 alpha[22] 65 alpha[23] 220 alpha[24] 450 alpha[25] 110 alpha[26] 3000 alpha[27] 79 alpha[28] 73 alpha[29] 240 alpha[30] 250 alpha[31] 240 alpha[32] 66 alpha[33] 100 alpha[34] 670 alpha[35] 63 alpha[36] 240 alpha[37] 230 alpha[38] 850 alpha[39] 98 alpha[40] 2700 alpha[41] 170 alpha[42] 220 alpha[43] 180 alpha[44] 100 alpha[45] 84 alpha[46] 220 alpha[47] 3000 alpha[48] 110 alpha[49] 65 alpha[50] 690 alpha[51] 190 alpha[52] 120 alpha[53] 340 alpha[54] 200 alpha[55] 82 alpha[56] 160 alpha[57] 130 alpha[58] 190 alpha[59] 3000 alpha[60] 320 alpha[61] 110 alpha[62] 110 alpha[63] 190 alpha[64] 150 alpha[65] 150 alpha[66] 740 alpha[67] 78 alpha[68] 360 alpha[69] 66 alpha[70] 420 alpha[71] 400 alpha[72] 110 alpha[73] 200 alpha[74] 70 alpha[75] 460 alpha[76] 230 alpha[77] 140 alpha[78] 3000 alpha[79] 61 alpha[80] 150 alpha[81] 230 alpha[82] 270 alpha[83] 200 alpha[84] 1900 alpha[85] 180 alpha[86] 97 alpha[87] 190 alpha[88] 430 alpha[89] 79 alpha[90] 490 alpha[91] 240 alpha[92] 850 alpha[93] 290 alpha[94] 140 alpha[95] 200 alpha[96] 72 alpha[97] 360 alpha[98] 530 alpha[99] 710 alpha[100] 59 alpha[101] 170 alpha[102] 120 alpha[103] 1600 alpha[104] 240 alpha[105] 230 alpha[106] 180 alpha[107] 480 alpha[108] 1600 [ reached getOption("max.print") -- omitted 412 rows ] For each parameter, n.eff is a crude measure of effective sample size, and Rhat is the potential scale reduction factor (at convergence, Rhat=1). DIC info (using the rule, pD = Dbar-Dhat) pD = 345.3 and DIC = 11034.3 DIC is an estimate of expected predictive error (lower deviance is better). |
out7を分析してみる。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 |
> out7$mean $mu [1] 2.083956 $beta1 [1] -0.02027451 $beta2 [1] 0.02040788 $alpha [1] -2.44106600 -2.10495957 0.36688000 -0.46156946 0.92599900 -2.71560633 [7] -1.24285017 0.75952422 -1.79170533 -0.44471666 1.01153910 1.21177320 [13] 0.59825199 -0.16966245 -0.60090641 0.38331842 0.18779839 0.59722578 [19] 1.41233593 0.47468410 0.24861063 -0.32752408 0.36233807 -2.49711063 [25] 0.59231646 0.07949163 0.78276763 1.40862257 -0.62965627 -1.84993810 [31] -0.46187545 1.13137690 1.84588100 -2.14640400 1.25870787 0.86176323 [37] 1.36548873 -2.57395317 0.30126482 0.92054207 -0.43966235 -0.30072689 [43] 1.16429953 1.70021067 1.21009672 -0.54487200 -2.83630967 1.12160613 [49] 0.84390780 0.83308943 -1.47225313 0.69578948 0.51704212 0.11066089 [55] 0.74350103 -1.36127330 1.86652400 1.30410273 1.00315886 -0.95065906 [61] 0.54271654 0.09487122 0.59594376 1.05902777 1.62004967 -1.59288587 [67] 1.15356713 -1.29677800 0.50304403 -1.59599617 -2.08396327 1.12175120 [73] 0.54441441 0.54116945 -1.53327788 -0.63383220 0.88038633 -2.83544833 [79] 1.07636957 -0.04144019 0.63479384 -0.44297300 0.50160417 1.15556122 [85] 0.80652607 0.94204513 0.99577310 1.13106057 0.91936560 0.50973400 [91] -0.43797829 0.58468842 0.70310967 0.28889478 -0.67390758 1.33187377 [97] 0.64688579 0.06822612 1.44448470 0.81112227 0.18159913 1.03838787 [103] -2.91245100 1.27062883 0.60414064 0.03084811 -2.30287607 -2.85209700 [109] -0.14564861 1.18344526 0.43876651 1.31574810 0.76769942 0.05540116 [115] 0.08878300 1.01302651 -1.37850017 0.02665341 0.56283542 0.73407563 [121] 0.88512195 0.03332699 -1.91827807 -2.20193270 -2.88932397 0.79424458 [127] 0.71751541 -2.44071633 -0.20864488 0.10615941 0.13504228 -2.15602767 [133] 0.49226899 -0.75962104 -2.51452613 0.52516485 1.84788167 0.42739547 [139] -0.52059221 0.14115342 0.81604128 1.29644960 -2.27191770 -2.62326300 [145] 0.32844966 1.03683229 0.03000885 0.30350421 1.51185740 -0.52959224 [151] 1.23265213 1.25396850 -0.07859709 -0.58965176 0.02485818 -0.10281508 [157] -2.26308660 -1.21915827 0.80876090 -2.59988133 0.73261783 -0.88968685 [163] 0.50890502 1.05651723 0.70893108 -1.27304299 -2.42868967 -1.50791060 [169] -0.54079960 1.21936340 -0.09604485 0.86428000 1.02026180 -1.81985970 [175] 0.42973296 -0.28434737 -2.75954600 -2.25876203 0.43165743 -1.87843787 [181] -0.62949180 0.83897210 -1.25107383 -0.42643814 -0.43475171 0.02991226 [187] 1.25361123 1.01509133 1.19173237 0.36962605 1.00657573 0.85030153 [193] 1.21873510 -0.27260000 0.35056476 0.32935906 -1.45381590 1.77962833 [199] -3.10941100 1.04887443 0.97190490 -1.72136437 0.68553774 -0.35649443 [205] -2.67914967 -0.14160519 1.09168773 0.45013128 0.73472321 -0.27718584 [211] 1.36080255 0.41049023 0.89281105 -1.73160430 0.67959678 1.25366650 [217] 0.79275292 1.03394203 0.25908805 0.98045282 -0.89408009 -3.15427900 [223] 0.45768517 -0.93698029 1.35263873 -0.65743918 -1.36982207 -2.46720697 [229] 0.97065513 1.17332227 1.41934297 1.37813240 1.59767917 1.52434660 [235] 1.75243200 $gamma [1] 0.0667672912 0.0198438103 -0.4989713254 0.0172686179 -0.2397118172 [6] 0.1872975526 0.0408389302 0.0895515805 -0.0633050190 -0.1160587978 [11] 0.0540076338 0.1731847838 -0.0198075047 0.3358718069 0.4376705556 [16] -0.2341689071 0.0820257198 0.0635486055 0.0006034248 -0.1068594987 [21] 0.0551394561 -0.3645931150 0.1549303322 0.0679018041 0.0895113007 [26] -0.3066040631 -0.2398677715 0.0761580437 -0.0914432474 -0.0361735038 [31] 0.1108270456 -0.4662317079 -0.0141490421 -0.5883828340 0.1750667738 [36] -0.0892119676 -0.3471762251 -0.0760849661 0.1205442560 -0.1395370163 [41] 0.2436989670 -0.1067899476 0.0445332397 0.2215683205 -0.1709514362 [46] -0.0315759201 0.0369095505 0.3266214047 -0.3248905661 0.1843246148 [51] -0.3334582044 -0.2873930748 -0.0174709533 0.0042127024 -0.2135077137 [56] 0.0009582513 -0.2311613228 0.0460226357 -0.0755827373 0.0347608392 [61] 0.3571709628 -0.2934868196 0.0488431453 0.0564526582 -0.1203483574 [66] -0.5386671880 -0.1396960282 0.1054598954 -0.0085994318 -0.1463131036 [71] 0.3298205373 0.1304540438 -0.5498881200 0.0683883630 -0.4238173714 [76] -0.3837453342 -0.1779757577 -0.3836162815 0.3437566733 0.2139462858 [81] -0.0689823561 -0.1525990310 -0.0659922187 -0.2015632550 -0.0414640776 [86] 0.0746613334 0.1141129278 0.0389238250 0.3972186626 -0.0302552018 [91] 0.2225845055 0.0382120725 -0.0373421054 -0.0724111251 0.0097654218 [96] -0.1682896849 0.1452131792 0.1569207836 0.0714490264 0.1322142055 [101] 0.2119538826 0.0834087912 0.0087001852 -0.1911443605 0.0303672926 [106] 0.0431275092 0.1012952343 0.2005482814 0.0405026925 -0.2193145390 [111] 0.3145653581 0.3326608409 0.2123800921 -0.1563304413 -0.6162820537 [116] 0.2508689428 0.5636267367 0.0962794405 -0.0179150199 0.0012329633 [121] 0.0695798239 0.0370107028 0.1971980728 0.3686271456 0.0441252673 [126] 0.1537099841 -0.2202558073 0.0646541776 0.0229385569 0.3148745023 [131] 0.2477141014 0.0723656917 0.4062794197 0.0432835497 -0.1425161149 [136] -0.2065212043 -0.0940589833 0.0587849863 -0.0006835738 0.0629237282 [141] 0.0504620239 0.1391740668 0.1616595838 0.0232445402 -0.0653626066 [146] -0.0887041425 0.0472880214 0.1031265110 -0.3933096356 0.1794525349 [151] 0.0329729586 -0.0283974124 0.0028765105 0.1382438643 0.0023819268 [156] 0.0781848479 0.0515688786 0.0480563870 -0.2425213302 -0.0867106914 [161] 0.1370762386 0.1998955026 0.0401405789 -0.1238674592 -0.4976051561 [166] 0.3539919633 0.0179490018 0.1240252720 0.0421211232 -0.1146528972 [171] 0.0859117126 0.0824844871 0.0859901923 0.0595824248 -0.1029606911 [176] 0.1053972135 -0.1018793412 0.3644587165 -0.1500970010 -0.0332910390 [181] -0.5033738386 -0.1388785218 -0.0846006074 0.1039169001 0.2087976810 [186] 0.0002436300 -0.1205603244 0.1144078425 -0.1903140171 -0.4313249620 [191] 0.1435783993 -0.0169932000 -0.4054698335 0.1873520925 -0.3450109861 [196] 0.1536834766 0.3015927771 0.1476881434 -0.0587879980 0.5785181100 [201] 0.0646962663 0.0032207132 -0.1333434150 -0.4199639275 0.2697604892 [206] -0.2116129318 -0.0162384006 -0.3074732693 -0.2982051441 -0.4995739603 [211] 0.1424363351 -0.1490902163 -0.0270796028 0.0498351449 0.0303694782 [216] 0.0243947350 -0.0561249745 0.0692241104 -0.0527108648 0.0064002711 [221] -0.2479301996 0.0477438916 0.1101964151 0.0342081855 0.0362546413 [226] -0.0215252230 0.0517109003 0.0943551552 0.0153586013 0.4571616481 [231] 0.0684976248 0.2954267358 0.0711746531 0.2515356069 0.2399796896 [236] 0.2568541780 -0.0300804373 -0.1319243292 0.3761978561 -0.1670316217 [241] -0.2455004989 0.5971190833 0.0487397740 0.2350626597 -0.0570349054 [246] 0.0491963137 0.0659248485 -0.3059029550 -0.2431238509 0.2788904844 [251] 0.2540709576 -0.0200673067 -0.3183696543 0.4193828764 -0.2441778786 [256] -0.1217179556 0.0731247358 -0.1414767015 -0.0388776083 -0.2702953770 [261] 0.1533726186 0.3154505782 -0.1425711547 -0.1501203620 0.3880106851 [266] -0.0272728727 0.0783324177 -0.0437081433 -0.1167622224 -0.5798829646 [271] 0.0260424658 -0.2566421794 $eps [1] -0.02409771 0.06694917 -0.15840634 -0.10449092 0.05521460 0.10194736 [7] 0.22630240 -0.13303958 -0.03263556 $sd.alpha [1] 1.302355 $sd.gamma [1] 0.3355838 $sd.eps [1] 0.1696964 $deviance [1] 10689.03 |
mu 2.083956
beta1 -0.02027451
beta2 0.02040788
モデルは
mu + beta1 * year[i] + beta2 * first[i,j] + alpha[j] + gamma[newobs[i,j]] + eps[i]
gamma[]は、272個のデータが含まれている。
newobs[i,j]とは忘れそうになるが、解析の当初に観測者に新たに連番で割り振ったID番号であるが、観測者データの欠損には272があてがわれた。
|
1 2 3 4 5 6 7 8 |
a <- as.numeric(levels(factor(obs))) # All the levels, numeric newobs <- obs # Gets ObsID from 1:271 for (j in 1:length(a)){newobs[which(obs==a[j])] <- j } table(newobs) newobs[is.na(newobs)] <- 272 table(newobs) first[is.na(first)] <- 0 table(first) |
235の観測サイトの調査には、どの観測者が担当したかのデータが含まれている。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
newobs obs1999 obs2000 obs2001 obs2002 obs2003 obs2004 obs2005 obs2006 obs2007 [1,] 61 61 61 61 61 61 61 61 156 [2,] 272 272 272 272 272 272 272 272 272 [3,] 272 143 143 143 256 256 256 256 256 [4,] 61 133 133 133 133 133 133 133 5 [5,] 121 121 121 121 121 121 121 121 121 ......... [106,] 47 47 47 47 192 192 192 192 192 [107,] 272 29 29 29 29 29 29 29 29 [108,] 272 272 272 272 272 272 272 272 272 [109,] 272 272 272 272 272 272 272 272 272 [110,] 173 173 173 173 173 173 173 173 173 [111,] 47 47 47 47 47 47 47 47 47 [ reached getOption("max.print") -- omitted 124 rows ] |
観察サイトにおける観察者の情報に基づくgamma[]指定は、例えば初年1999年は以下のように指定できる
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 |
> out7$mean$gamma[newobs[,1]] [1] 0.3571709628 -0.2566421794 -0.2566421794 0.3571709628 0.0695798239 [6] -0.2566421794 -0.2479301996 -0.2479301996 0.1731847838 0.1031265110 [11] 0.2954267358 0.3358718069 0.0515688786 -0.2455004989 0.1031265110 [16] 0.0362546413 0.2350626597 0.0179490018 0.3298205373 0.0477438916 [21] -0.0198075047 0.4062794197 -0.1779757577 -0.1709514362 0.1872975526 [26] 0.0028765105 0.2954267358 0.1731847838 0.0943551552 0.0064002711 [31] 0.0432835497 0.2119538826 0.1304540438 -0.0085994318 0.4062794197 [36] 0.0943551552 0.0064002711 -0.2566421794 0.1794525349 0.0711746531 [41] 0.3145653581 0.1304540438 -0.2566421794 0.3298205373 0.0723656917 [46] -0.0867106914 -0.2566421794 0.3298205373 0.3571709628 0.0746613334 [51] -0.0215252230 0.0303694782 0.0460226357 0.5636267367 0.0172686179 [56] 0.2119538826 -0.2566421794 -0.2873930748 0.0009582513 -0.2566421794 [61] 0.3326608409 0.2436989670 0.4571616481 0.0564526582 -0.2566421794 [66] -0.2566421794 0.3326608409 -0.2566421794 0.1382438643 -0.2311613228 [71] -0.0892119676 -0.3471762251 0.0421211232 0.2123800921 -0.0940589833 [76] -0.2566421794 -0.2566421794 -0.2566421794 0.0369095505 0.0487397740 [81] 0.0595824248 0.3686271456 -0.2873930748 0.1101964151 -0.2566421794 [86] 0.0369095505 0.0487397740 -0.0006835738 0.0369095505 0.0370107028 [91] -0.0283974124 0.0389238250 -0.2566421794 0.0097654218 0.3148745023 [96] 0.1569207836 -0.2566421794 0.0198438103 0.1205442560 0.0369095505 [101] 0.0369095505 0.2399796896 -0.1911443605 0.0824844871 -0.2566421794 [106] 0.0369095505 -0.2566421794 -0.2566421794 -0.2566421794 0.0859901923 [111] 0.0369095505 0.0834087912 -0.2566421794 -0.2566421794 -0.2566421794 [116] 0.0347608392 0.1141129278 0.1322142055 -0.2566421794 -0.5498881200 [121] -0.1067899476 -0.0414640776 -0.1425161149 -0.1563304413 -0.2015632550 [126] -0.0689823561 -0.3066040631 -0.0653626066 -0.0300804373 0.0441252673 [131] 0.2225845055 0.1569207836 0.0012329633 -0.0659922187 -0.1670316217 [136] 0.0629237282 -0.2566421794 0.0329729586 0.2215683205 0.3437566733 [141] 0.0517109003 -0.2566421794 -0.1396960282 -0.2566421794 0.0012329633 [146] 0.0504620239 -0.2566421794 -0.2566421794 -0.2566421794 -0.1525990310 [151] -0.3334582044 -0.2566421794 -0.1160587978 0.0683883630 -0.2934868196 [156] -0.6162820537 -0.2566421794 0.0895515805 0.0498351449 -0.2566421794 [161] -0.2566421794 -0.2566421794 -0.2566421794 -0.2341689071 0.0635486055 [166] 0.0480563870 -0.2566421794 -0.2566421794 -0.2566421794 -0.2566421794 [171] 0.0042127024 0.0445332397 -0.1319243292 0.3761978561 -0.0174709533 [176] -0.2566421794 0.0540076338 -0.2566421794 0.0342081855 -0.1525990310 [181] 0.5971190833 -0.0755827373 -0.2566421794 -0.2566421794 -0.1682896849 [186] 0.0153586013 0.0684976248 0.1569207836 0.0488431453 -0.2566421794 [191] 0.1569207836 -0.2566421794 0.1391740668 -0.1682896849 -0.2566421794 [196] -0.2566421794 -0.1068594987 -0.2566421794 -0.2566421794 0.0859117126 [201] -0.2566421794 -0.1203483574 -0.3836162815 -0.4989713254 0.0023819268 [206] -0.0302552018 -0.0373421054 0.0408389302 0.2568541780 0.0023819268 [211] 0.0820257198 0.0303672926 0.0646541776 -0.1146528972 -0.2566421794 [216] -0.2566421794 0.0405026925 0.1537099841 0.1549303322 0.0679018041 [221] -0.0633050190 -0.2202558073 -0.0570349054 -0.2566421794 0.1012952343 [226] -0.0527108648 -0.2566421794 -0.0315759201 -0.2566421794 0.0692241104 [231] 0.0761580437 -0.2398677715 -0.0174709533 -0.2566421794 -0.2566421794 |
そこで年度ごとのデータをモデル式に挿入すると、
|
1 2 3 4 5 6 7 8 9 10 11 |
> y1999_w <- out7$mean$mu + out7$mean$beta1*year[1] + out7$mean$beta2*first[,1] + out7$mean$alpha + out7$mean$gamma[newobs[,1]] + out7$mean$eps[1] > y2000_w <- out7$mean$mu + out7$mean$beta1*year[2] + out7$mean$beta2*first[,2] + out7$mean$alpha + out7$mean$gamma[newobs[,2]] + out7$mean$eps[2] > y2001_w <- out7$mean$mu + out7$mean$beta1*year[3] + out7$mean$beta2*first[,3] + out7$mean$alpha + out7$mean$gamma[newobs[,3]] + out7$mean$eps[3] > y2002_w <- out7$mean$mu + out7$mean$beta1*year[4] + out7$mean$beta2*first[,4] + out7$mean$alpha + out7$mean$gamma[newobs[,4]] + out7$mean$eps[4] > y2003_w <- out7$mean$mu + out7$mean$beta1*year[5] + out7$mean$beta2*first[,5] + out7$mean$alpha + out7$mean$gamma[newobs[,5]] + out7$mean$eps[5] > y2004_w <- out7$mean$mu + out7$mean$beta1*year[6] + out7$mean$beta2*first[,6] + out7$mean$alpha + out7$mean$gamma[newobs[,6]] + out7$mean$eps[6] > y2005_w <- out7$mean$mu + out7$mean$beta1*year[7] + out7$mean$beta2*first[,7] + out7$mean$alpha + out7$mean$gamma[newobs[,7]] + out7$mean$eps[7] > y2006_w <- out7$mean$mu + out7$mean$beta1*year[8] + out7$mean$beta2*first[,8] + out7$mean$alpha + out7$mean$gamma[newobs[,8]] + out7$mean$eps[8] > y2007_w <- out7$mean$mu + out7$mean$beta1*year[9] + out7$mean$beta2*first[,9] + out7$mean$alpha + out7$mean$gamma[newobs[,9]] + out7$mean$eps[9] > boxplot(exp(y1999_w), exp(y2000_w), exp(y2001_w), exp(y2002_w), exp(y2003_w), exp(y2004_w), exp(y2005_w), exp(y2006_w), exp(y2007_w), names=c(1999:2007)) > + boxplot(exp(y1999_v), exp(y2000_v), exp(y2001_v), exp(y2002_v), exp(y2003_v), exp(y2004_v), exp(y2005_v), exp(y2006_v), exp(y2007_v), names=c(1999:2007)) |
前回と、調査差のランダム効果を含めた今回を並べて比較してみる。
|
1 |
> boxplot(exp(y1999_v), exp(y1999_w), exp(y2000_v), exp(y2000_w), exp(y2001_v), exp(y2001_w), exp(y2002_v), exp(y2002_w), exp(y2003_v), exp(y2003_w), exp(y2004_v), exp(y2004_w), exp(y2005_v), exp(y2005_w), exp(y2006_v), exp(y2006_w), exp(y2007_v), exp(y2007_w), names=c(1999, 1999, 2000, 2000, 2001, 2001, 2002, 2002, 2003, 2003, 2004, 2004, 2005, 2005, 2006, 2006, 2007, 2007)) |