BPA BUGSで学ぶ階層モデリング Baysian Population Analysis Using WinBUGS, Marc Kery & Michael Schaubの学習ノート
——————————————————————
ポアソンGLMの例として、i年計測値Ciをモデル化する。
以下に単一の共変量Xがある場合の年iにおける計測数CiのポアソンGLMを代数記述する。
1. 応答変数のランダムな部分(統計分布)
Ci ? Poisson(λi)
2. リンク関数と系統的な部分(対数リンク関数)
log(λi)=ηi
3. 応答の系統的な部分(線形予測子ηi)
ηi = α + β * Xi
ここでは、λiは、算術軸上での年iにおける計数値の期待値(応答変数の平均)
ηiは、対数軸上での年iにおける計数値の期待値
Xiは、年iにおける共変量Xの値
αとβは、この共変量と計数値との線形対数回帰における2つのパラメータ
以下、シミュレーションで生成された仮想データと、実際のデータセットを使用したポアソンGLMデータの生成と解析例を示す。
3.3.1 仮想データの生成と解析
ハヤブサ(Falco peregrinus)のある個体群の計数値データを生成する関数を定義する。データはポアソン分布に従い、n年に渡る。ここで、パラメータは実際のデータを元にしている。
線形予測子には、時間に関する三次元多項関数
ηi = α + β1 * Xi^1 + β2 * Xi^2 + β3 * Xi^3
以下、まず頻度主義のGLMを示し、続いてベイズ主義でのGLMを示す。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 |
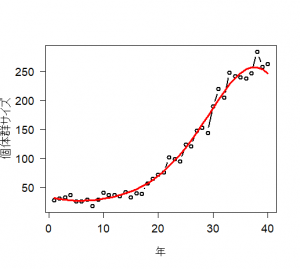
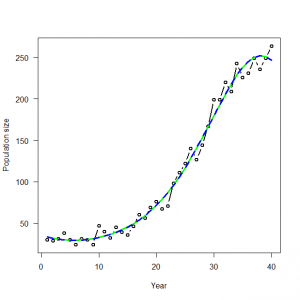
# 3.3. Poisson GLM in R and WinBUGS for modeling times series of counts # 3.3.1. Generation and analysis of simulated data data.fn <- function(n = 40, alpha = 3.5576, beta1 = -0.0912, beta2 = 0.0091, beta3 = -0.00014){ # n: Number of years #調査年数 # alpha, beta1, beta2, beta3: coefficients of a #年に対する計数値の三次元多項式の係数 # cubic polynomial of count on year #時間の共変量の値を生成 # Generate values of time covariate year <- 1:n #信号:GLMの系統的な部分を生成 # Signal: Build up systematic part of the GLM log.expected.count <- alpha + beta1 * year + beta2 * year^2 + beta3 * year^3 expected.count <- exp(log.expected.count) #ノイズ:GLMのランダムな部分を生成 #GLM:計数値の期待値のまわりのポアソン分布ノイズ # Noise: generate random part of the GLM: Poisson noise around expected counts C <- rpois(n = n, lambda = expected.count) #シミュレーションで生成された仮想データを作図する # Plot simulated data plot(year, C, type = "b", lwd = 2, col = "black", main = "", las = 1, ylab = "Population size", xlab = "Year", cex.lab = 1.2, cex.axis = 1.2) lines(year, expected.count, type = "l", lwd = 3, col = "red") return(list(n = n, alpha = alpha, beta1 = beta1, beta2 = beta2, beta3 = beta3, year = year, expected.count = expected.count, C = C)) } |
実際にRで上記コードを動かしてみると、
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
> # 3.3. Poisson GLM in R and WinBUGS for modeling times series of counts > # 3.3.1. Generation and analysis of simulated data > data.fn <- function(n = 40, alpha = 3.5576, beta1 = -0.0912, beta2 = 0.0091, beta3 = -0.00014){ + # n: Number of years + # alpha, beta1, beta2, beta3: coefficients of a + # cubic polynomial of count on year + + # Generate values of time covariate + year <- 1:n + + # Signal: Build up systematic part of the GLM + log.expected.count <- alpha + beta1 * year + beta2 * year^2 + beta3 * year^3 + expected.count <- exp(log.expected.count) + + # Noise: generate random part of the GLM: Poisson noise around expected counts + C <- rpois(n = n, lambda = expected.count) + + # Plot simulated data + plot(year, C, type = "b", lwd = 2, col = "black", main = "", las = 1, ylab = "個体群サイズ", xlab = "年", cex.lab = 1.2, cex.axis = 1.2) + lines(year, expected.count, type = "l", lwd = 3, col = "red") + + return(list(n = n, alpha = alpha, beta1 = beta1, beta2 = beta2, beta3 = beta3, year = year, expected.count = expected.count, C = C)) + } > > data <- data.fn() Hit <Return> to see next plot: |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
> fm <- glm(C ~ year + I(year^2) + I(year^3), family = poisson, data = data) > summary(fm) Call: glm(formula = C ~ year + I(year^2) + I(year^3), family = poisson, data = data) Deviance Residuals: Min 1Q Median 3Q Max -2.10679 -0.59098 0.03127 0.49605 1.79249 Coefficients: Estimate Std. Error z value Pr(>|z|) (Intercept) 3.590e+00 1.133e-01 31.685 < 2e-16 *** year -9.337e-02 1.985e-02 -4.704 2.56e-06 *** I(year^2) 9.000e-03 9.879e-04 9.110 < 2e-16 *** I(year^3) -1.360e-04 1.443e-05 -9.423 < 2e-16 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 (Dispersion parameter for poisson family taken to be 1) Null deviance: 2691.615 on 39 degrees of freedom Residual deviance: 38.148 on 36 degrees of freedom AIC: 294.29 Number of Fisher Scoring iterations: 4 |
dataの中身を覗いてみる
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
> data $n [1] 40 $alpha [1] 3.5576 $beta1 [1] -0.0912 $beta2 [1] 0.0091 $beta3 [1] -0.00014 $year [1] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 [27] 27 28 29 30 31 32 33 34 35 36 37 38 39 40 $expected.count [1] 32.30946 30.27978 28.85029 27.92270 27.42898 27.32385 27.57970 [8] 28.18303 29.13208 30.43521 32.10976 34.18134 36.68324 39.65591 [15] 43.14644 47.20784 51.89799 57.27819 63.41117 70.35825 78.17579 [22] 86.91060 96.59433 107.23686 118.81884 131.28362 144.52897 158.39945 [29] 172.67997 187.09191 201.29269 214.88006 227.40214 238.37379 247.29946 [36] 253.70191 257.15525 257.31989 253.97606 247.05229 $C [1] 28 31 33 37 26 26 29 18 29 41 37 37 35 42 33 40 39 57 65 [20] 72 76 102 99 95 124 121 148 153 144 190 220 205 248 242 240 238 247 284 [39] 258 263 |
まずはsink()関数について、理解しておこう。
R コマンドの実行結果はデフォルトではウィンドウ (console) 内に表示されますが、下記のようにして任意のファイルに出力先を切り替えることができます。
> sink(“output.txt”)
出力先をウィンドウ (console) に戻すには、パラメータ無しで以下のように実行します。
> sink()
では、次にベイズ流解析を示そう。
そのままでは、共変量xiが40^3=64000となり、数値がオーバーフローを引き起こすようだ。
そこで、共変量の中央化や標準化を行う。ここでは、平均を引き、標準偏差で割る。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
> # Specify model in BUGS language > sink("GLM_Poisson.txt") > cat(" + model { + + # Priors + alpha ~ dunif(-20, 20) + beta1 ~ dunif(-10, 10) + beta2 ~ dunif(-10, 10) + beta3 ~ dunif(-10, 10) + + # Likelihood: Note key components of a GLM on one line each + for (i in 1:n){ + C[i] ~ dpois(lambda[i]) # 1. Distribution for random part + log(lambda[i]) <- log.lambda[i] # 2. Link function + log.lambda[i] <- alpha + beta1 * year[i] + beta2 * pow(year[i],2) + beta3 * pow(year[i],3) # 3. Linear predictor + } #i + } + ",fill = TRUE) > sink() > > # Initial values > inits <- function() list(alpha = runif(1, -2, 2), beta1 = runif(1, -3, 3)) > > # Parameters monitored > params <- c("alpha", "beta1", "beta2", "beta3", "lambda") > > # MCMC settings > ni <- 2000 > nt <- 2 > nb <- 1000 > nc <- 3 |
|
1 2 3 4 5 6 7 |
> # Bundle data > mean.year <- mean(data$year) # Mean of year covariate > sd.year <- sd(data$year) # SD of year covariate > win.data <- list(C = data$C, n = length(data$C), year = (data$year - mean.year) / sd.year) > > # Call WinBUGS from R (BRT < 1 min) > out <- bugs(data = win.data, inits = inits, parameters.to.save = params, model.file = "GLM_Poisson.txt", n.chains = nc, n.thin = nt, n.iter = ni, n.burnin = nb, debug = TRUE, bugs.directory = bugs.dir, working.directory = getwd()) |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 |
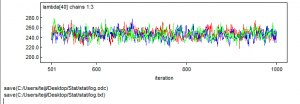
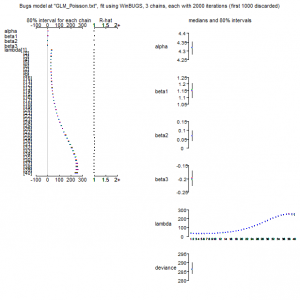
> print(out, dig = 3) Inference for Bugs model at "GLM_Poisson.txt", fit using WinBUGS, 3 chains, each with 2000 iterations (first 1000 discarded), n.thin = 2 n.sims = 1500 iterations saved mean sd 2.5% 25% 50% 75% 97.5% Rhat n.eff alpha 4.318 0.028 4.262 4.300 4.317 4.336 4.373 1.002 1000 beta1 1.151 0.043 1.062 1.124 1.151 1.181 1.232 1.020 100 beta2 0.069 0.023 0.022 0.054 0.069 0.084 0.114 1.006 450 beta3 -0.198 0.023 -0.241 -0.214 -0.200 -0.184 -0.150 1.020 100 lambda[1] 33.599 3.210 27.644 31.417 33.505 35.752 40.025 1.007 310 lambda[2] 31.755 2.593 26.895 30.027 31.630 33.442 37.021 1.006 370 lambda[3] 30.469 2.131 26.410 29.057 30.400 31.882 34.680 1.005 450 lambda[4] 29.658 1.792 26.255 28.447 29.605 30.840 33.220 1.004 530 lambda[5] 29.260 1.552 26.355 28.187 29.225 30.250 32.375 1.004 560 lambda[6] 29.238 1.394 26.629 28.267 29.200 30.120 32.056 1.004 500 lambda[7] 29.565 1.305 27.165 28.670 29.530 30.430 32.230 1.005 390 lambda[8] 30.231 1.270 27.945 29.340 30.190 31.080 32.845 1.007 310 lambda[9] 31.235 1.277 28.884 30.320 31.185 32.060 33.860 1.008 260 lambda[10] 32.582 1.314 30.160 31.650 32.560 33.450 35.330 1.009 230 lambda[11] 34.291 1.372 31.770 33.320 34.260 35.182 37.170 1.010 210 lambda[12] 36.381 1.443 33.715 35.360 36.360 37.330 39.381 1.010 210 lambda[13] 38.884 1.522 36.050 37.800 38.870 39.872 42.045 1.010 210 lambda[14] 41.832 1.604 38.845 40.710 41.805 42.850 45.160 1.009 220 lambda[15] 45.269 1.687 42.080 44.097 45.235 46.340 48.755 1.009 240 lambda[16] 49.237 1.769 45.890 48.030 49.190 50.350 52.896 1.008 270 lambda[17] 53.788 1.847 50.320 52.557 53.720 54.960 57.595 1.006 310 lambda[18] 58.971 1.921 55.400 57.717 58.935 60.220 62.891 1.005 390 lambda[19] 64.840 1.991 61.100 63.530 64.800 66.130 68.901 1.004 520 lambda[20] 71.445 2.060 67.500 70.110 71.430 72.780 75.651 1.003 790 lambda[21] 78.832 2.133 74.694 77.440 78.810 80.222 83.111 1.001 1400 lambda[22] 87.038 2.216 82.709 85.587 86.985 88.505 91.420 1.001 1500 lambda[23] 96.089 2.321 91.528 94.520 96.080 97.620 100.700 1.001 1500 lambda[24] 105.991 2.454 101.200 104.400 106.000 107.600 110.900 1.002 1300 lambda[25] 116.725 2.631 111.700 115.000 116.700 118.500 121.900 1.003 650 lambda[26] 128.249 2.849 122.847 126.300 128.200 130.100 133.952 1.006 360 lambda[27] 140.476 3.109 134.600 138.400 140.400 142.600 146.600 1.008 250 lambda[28] 153.276 3.396 146.747 151.075 153.100 155.600 160.152 1.010 200 lambda[29] 166.480 3.693 159.347 164.000 166.350 169.000 173.800 1.012 170 lambda[30] 179.859 3.975 172.147 177.200 179.800 182.500 187.852 1.013 150 lambda[31] 193.138 4.214 184.895 190.300 193.000 195.800 201.557 1.014 150 lambda[32] 205.986 4.386 197.447 203.100 205.900 208.800 214.652 1.014 150 lambda[33] 218.030 4.485 209.300 215.100 217.900 220.900 226.900 1.012 170 lambda[34] 228.869 4.528 220.047 225.800 228.600 231.700 238.200 1.009 220 lambda[35] 238.081 4.592 229.347 235.000 237.800 241.100 247.552 1.006 360 lambda[36] 245.252 4.817 236.300 241.900 245.000 248.325 255.152 1.002 1100 lambda[37] 249.997 5.380 239.947 246.200 249.800 253.700 260.852 1.001 1500 lambda[38] 251.987 6.405 239.995 247.300 251.950 256.300 264.752 1.003 690 lambda[39] 250.973 7.903 236.500 245.375 250.800 256.500 266.400 1.006 310 lambda[40] 246.816 9.783 228.795 239.800 246.800 253.600 266.052 1.010 200 deviance 286.722 2.766 283.400 284.600 286.100 288.200 294.000 1.002 840 For each parameter, n.eff is a crude measure of effective sample size, and Rhat is the potential scale reduction factor (at convergence, Rhat=1). DIC info (using the rule, pD = Dbar-Dhat) pD = 3.9 and DIC = 290.6 DIC is an estimate of expected predictive error (lower deviance is better). |
|
1 |
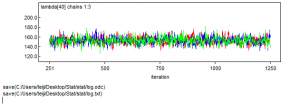
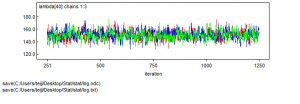
> plot(out) |
|
1 2 3 4 5 6 7 8 |
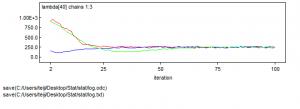
> # New MCMC settings with essentially no burnin > ni <- 100 > nt <- 1 > nb <- 1 > > # Call WinBUGS from R (BRT < 1 min) > tmp <- bugs(data = win.data, inits = inits, parameters.to.save = params, model.file = "GLM_Poisson.txt", n.chains = nc, n.thin = nt, n.iter = ni, n.burnin = nb, debug = TRUE, bugs.directory = bugs.dir, working.directory = getwd()) > |
|
1 2 3 4 5 |
> plot(1:40, data$C, type = "b", lwd = 2, col = "black", main = "", las = 1, ylab = "Population size", xlab = "Year") > R.predictions <- predict(glm(C ~ year + I(year^2) + I(year^3), family = poisson, data = data), type = "response") > lines(1:40, R.predictions, type = "l", lwd = 3, col = "green") > WinBUGS.predictions <- out$mean$lambda > lines(1:40, WinBUGS.predictions, type = "l", lwd = 3, col = "blue", lty = 2) |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 |
> cbind(R.predictions, WinBUGS.predictions) R.predictions WinBUGS.predictions 1 33.41527 33.59892 2 31.65689 31.75460 3 30.43349 30.46943 4 29.66708 29.65756 5 29.30334 29.26017 6 29.30611 29.23756 7 29.65361 29.56511 8 30.33575 30.23124 9 31.35230 31.23466 10 32.71155 32.58248 11 34.42940 34.29077 12 36.52867 36.38124 13 39.03858 38.88356 14 41.99420 41.83248 15 45.43594 45.26855 16 49.40878 49.23746 17 53.96133 53.78794 18 59.14454 58.97142 19 65.00993 64.84036 20 71.60732 71.44528 21 78.98185 78.83193 22 87.17039 87.03809 23 96.19709 96.08892 24 106.06834 105.99094 25 116.76699 116.72493 26 128.24615 128.24907 27 140.42298 140.47560 28 153.17263 153.27633 29 166.32319 166.47960 30 179.65227 179.85920 31 192.88587 193.13760 32 205.70058 205.98587 33 217.72962 218.02987 34 228.57358 228.86880 35 237.81574 238.08093 36 245.04215 245.25160 37 249.86542 249.99733 38 251.95111 251.98687 39 251.04448 250.97307 40 246.99546 246.81600 |
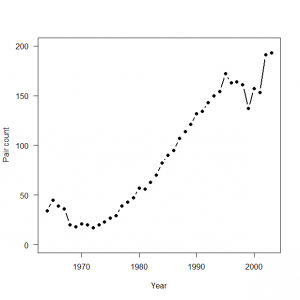
3.3.2 実際のデータセットの解析
|
1 2 3 4 5 6 |
> # 3.3.2. Analysis of real data set > # Read data > peregrine <- read.table("falcons.txt", header = TRUE) > attach(peregrine) > > plot(Year, Pairs, type = "b", lwd = 2, main = "", las = 1, ylab = "Pair count", xlab = "Year", ylim = c(0, 200), pch = 16) |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
> # Bundle data > mean.year <- mean(1:length(Year)) # Mean of year covariate > sd.year <- sd(1:length(Year)) # SD of year covariate > win.data <- list(C = Pairs, n = length(Pairs), year = (1: length(Year) - mean.year) / sd.year) > > # Initial values > inits <- function() list(alpha = runif(1, -2, 2), beta1 = runif(1, -3, 3)) > > # Parameters monitored > params <- c("alpha", "beta1", "beta2", "beta3", "lambda") > > # MCMC settings > ni <- 2500 > nt <- 2 > nb <- 500 > nc <- 3 > > # Call WinBUGS from R (BRT < 1 min) > out1 <- bugs(data = win.data, inits = inits, parameters.to.save = params, model.file = "GLM_Poisson.txt", n.chains = nc, n.thin = nt, n.iter = ni, n.burnin = nb, debug = TRUE, bugs.directory = bugs.dir, working.directory = getwd()) |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 |
> # Summarize posteriors > print(out1, dig = 3) Inference for Bugs model at "GLM_Poisson.txt", fit using WinBUGS, 3 chains, each with 2500 iterations (first 500 discarded), n.thin = 2 n.sims = 3000 iterations saved mean sd 2.5% 25% 50% 75% 97.5% Rhat n.eff alpha 4.232 0.028 4.176 4.214 4.233 4.251 4.286 1.002 1700 beta1 1.116 0.045 1.030 1.087 1.115 1.146 1.204 1.001 2800 beta2 0.006 0.023 -0.041 -0.009 0.006 0.021 0.050 1.002 1400 beta3 -0.233 0.024 -0.281 -0.249 -0.234 -0.218 -0.188 1.001 3000 lambda[1] 32.301 3.119 26.479 30.120 32.170 34.400 38.591 1.001 2600 lambda[2] 30.250 2.506 25.530 28.507 30.145 31.900 35.330 1.001 2400 lambda[3] 28.804 2.056 24.949 27.390 28.720 30.190 32.980 1.001 2100 lambda[4] 27.861 1.729 24.540 26.670 27.820 29.020 31.280 1.002 1900 lambda[5] 27.348 1.501 24.470 26.310 27.320 28.360 30.310 1.002 1800 lambda[6] 27.219 1.351 24.630 26.290 27.170 28.170 29.820 1.002 1700 lambda[7] 27.442 1.263 25.010 26.580 27.430 28.310 29.980 1.002 1600 lambda[8] 28.000 1.224 25.600 27.160 27.980 28.850 30.450 1.002 1600 lambda[9] 28.888 1.222 26.489 28.050 28.880 29.730 31.300 1.002 1600 lambda[10] 30.109 1.246 27.710 29.250 30.090 30.960 32.560 1.002 1600 lambda[11] 31.675 1.289 29.170 30.800 31.670 32.542 34.220 1.002 1700 lambda[12] 33.604 1.344 30.990 32.700 33.590 34.502 36.210 1.002 1700 lambda[13] 35.920 1.406 33.180 34.980 35.890 36.860 38.660 1.002 1700 lambda[14] 38.652 1.473 35.760 37.660 38.605 39.620 41.510 1.002 1700 lambda[15] 41.833 1.542 38.820 40.810 41.810 42.860 44.770 1.002 1700 lambda[16] 45.497 1.610 42.350 44.400 45.480 46.580 48.590 1.002 1700 lambda[17] 49.683 1.677 46.399 48.570 49.670 50.822 52.900 1.002 1700 lambda[18] 54.425 1.744 50.980 53.270 54.430 55.590 57.860 1.002 1700 lambda[19] 59.756 1.812 56.230 58.570 59.770 60.990 63.360 1.002 1700 lambda[20] 65.701 1.886 62.029 64.467 65.720 66.970 69.460 1.002 1700 lambda[21] 72.276 1.970 68.410 70.980 72.310 73.600 76.111 1.002 1700 lambda[22] 79.483 2.074 75.449 78.100 79.530 80.870 83.611 1.002 1800 lambda[23] 87.302 2.205 83.069 85.770 87.370 88.740 91.700 1.001 2000 lambda[24] 95.689 2.370 91.100 94.100 95.710 97.252 100.500 1.001 2300 lambda[25] 104.572 2.572 99.599 102.800 104.600 106.300 109.800 1.001 2700 lambda[26] 113.840 2.808 108.397 111.900 113.800 115.700 119.402 1.001 3000 lambda[27] 123.344 3.068 117.200 121.300 123.300 125.400 129.500 1.001 3000 lambda[28] 132.897 3.335 126.300 130.600 132.900 135.100 139.500 1.001 3000 lambda[29] 142.262 3.590 135.297 139.900 142.300 144.600 149.400 1.001 3000 lambda[30] 151.171 3.807 143.700 148.675 151.200 153.600 158.900 1.001 3000 lambda[31] 159.320 3.968 151.597 156.700 159.300 161.900 167.200 1.001 3000 lambda[32] 166.384 4.058 158.497 163.675 166.400 169.000 174.500 1.001 3000 lambda[33] 172.035 4.084 164.000 169.300 172.000 174.800 180.100 1.001 3000 lambda[34] 175.957 4.078 168.100 173.100 175.900 178.700 184.200 1.001 3000 lambda[35] 177.868 4.110 169.900 175.075 177.800 180.625 186.000 1.001 3000 lambda[36] 177.552 4.287 169.200 174.600 177.600 180.400 185.800 1.001 3000 lambda[37] 174.870 4.700 165.800 171.700 174.900 177.900 184.100 1.001 3000 lambda[38] 169.783 5.385 159.400 166.175 169.900 173.300 180.400 1.001 3000 lambda[39] 162.368 6.293 150.200 158.100 162.400 166.500 174.800 1.001 3000 lambda[40] 152.818 7.328 138.897 147.800 152.800 157.700 167.500 1.001 3000 deviance 322.233 2.770 318.800 320.300 321.600 323.600 328.900 1.001 3000 For each parameter, n.eff is a crude measure of effective sample size, and Rhat is the potential scale reduction factor (at convergence, Rhat=1). DIC info (using the rule, pD = Dbar-Dhat) pD = 3.9 and DIC = 326.1 DIC is an estimate of expected predictive error (lower deviance is better). |
|
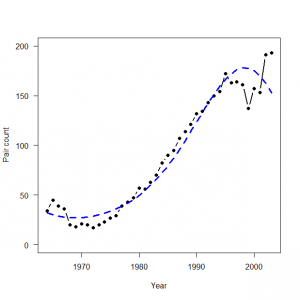
1 2 |
> WinBUGS.predictions <- out1$mean$lambda > lines(Year, WinBUGS.predictions, type = "l", lwd = 3, col = "blue", lty = 2) |
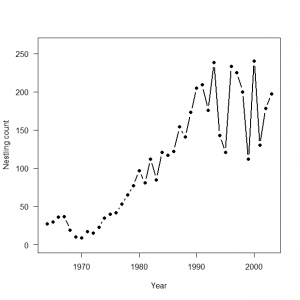
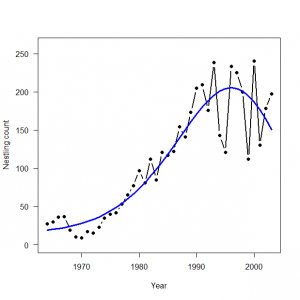
3.4 産仔数のモデリング:ポアソンGLM
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
> # 3.4. Poisson GLM for modeling fecundity > plot(Year, Eyasses, type = "b", lwd = 2, main = "", las = 1, ylab = "Nestling count", xlab = "Year", ylim = c(0, 260), pch = 16) > > # Bundle data > mean.year <- mean(1:length(Year)) # Mean of year covariate > sd.year <- sd(1:length(Year)) # SD of year covariate > win.data <- list(C = Eyasses, n = length(Eyasses), year = (1: length(Year) - mean.year) / sd.year) > > # Call WinBUGS from R (BRT < 1 min) > out2 <- bugs(data = win.data, inits = inits, parameters.to.save = params, model.file = "GLM_Poisson.txt", n.chains = nc, n.thin = nt, n.iter = ni, n.burnin = nb, debug = TRUE, bugs.directory = bugs.dir, working.directory = getwd()) > > # Plot predictions > WinBUGS.predictions <- out2$mean$lambda > lines(Year, WinBUGS.predictions, type = "l", lwd = 3, col = "blue") |
3.5 上限のある計数値データのモデリング;二項GLM
二項GLMの例として、年iにおける全観測つがい数(Ni)中の繁殖成功つがい数(Ci) を40年全体を対象としてモデル化する。
1. 応答のうちのランダムな部分(統計分布)
Ci ~ Ninomial(Ni, pi)
2. ランダムな部分と系統的な部分のリンク(ロジットリンク関数)
logit(pi) = log(pi/(1-pi) = ηi
3. 応答のうちの系統的な部分(線形予測子ηi)
ηi = α + β1 * Xi + β2 * Xi^2
ここでpiは、算術軸上での成功つがい数の割合の期待値であり、Ni回試行それぞれに対する応答の平均である。ηiは、それと同じ割合をロジットリンク軸としたもの。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
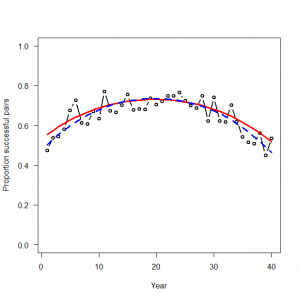
> # 3.5. Binomial GLM for modeling bounded counts or proportions > # 3.5.1. Generation and analysis of simulated data > data.fn <- function(nyears = 40, alpha = 0, beta1 = -0.1, beta2 = -0.9){ + # nyears: Number of years + # alpha, beta1, beta2: coefficients + + # Generate untransformed and transformed values of time covariate + year <- 1:nyears + YR <- (year-round(nyears/2)) / (nyears / 2) + + # Generate values of binomial totals (N) + N <- round(runif(nyears, min = 20, max = 100)) + + # Signal: build up systematic part of the GLM + exp.p <- plogis(alpha + beta1 * YR + beta2 * (YR^2)) + + # Noise: generate random part of the GLM: Binomial noise around expected counts (which is N) + C <- rbinom(n = nyears, size = N, prob = exp.p) + + # Plot simulated data + plot(year, C/N, type = "b", lwd = 2, col = "black", main = "", las = 1, ylab = "Proportion successful pairs", xlab = "Year", ylim = c(0, 1)) + points(year, exp.p, type = "l", lwd = 3, col = "red") + + return(list(nyears = nyears, alpha = alpha, beta1 = beta1, beta2 = beta2, year = year, YR = YR, exp.p = exp.p, C = C, N = N)) + } > > data <- data.fn(nyears = 40, alpha = 1, beta1 = -0.03, beta2 = -0.9) |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
> # Specify model in BUGS language > sink("GLM_Binomial.txt") > cat(" + model { + + # Priors + alpha ~ dnorm(0, 0.001) + beta1 ~ dnorm(0, 0.001) + beta2 ~ dnorm(0, 0.001) + + # Likelihood + for (i in 1:nyears){ + C[i] ~ dbin(p[i], N[i]) # 1. Distribution for random part + logit(p[i]) <- alpha + beta1 * year[i] + beta2 * pow(year[i],2) # link function and linear predictor + } + } + ",fill = TRUE) > sink() |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
> # Bundle data > win.data <- list(C = data$C, N = data$N, nyears = length(data$C), year = data$YR) > > # Initial values > inits <- function() list(alpha = runif(1, -1, 1), beta1 = runif(1, -1, 1), beta2 = runif(1, -1, 1)) > > # Parameters monitored > params <- c("alpha", "beta1", "beta2", "p") > > # MCMC settings > ni <- 2500 > nt <- 2 > nb <- 500 > nc <- 3 > # Call WinBUGS from R (BRT < 1 min) > out <- bugs(data = win.data, inits = inits, parameters.to.save = params, model.file = "GLM_Binomial.txt", n.chains = nc, n.thin = nt, n.iter = ni, n.burnin = nb, debug = TRUE, bugs.directory = bugs.dir, working.directory = getwd()) > # Plot predictions > WinBUGS.predictions <- out$mean$p > lines(1:length(data$C), WinBUGS.predictions, type = "l", lwd = 3, col = "blue", lty = 2) > |
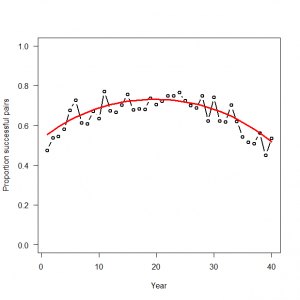
3.5.2 実際のデータセットの解析
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
> # 3.5.2. Analysis of real data set > # Read data and attach them > peregrine <- read.table("falcons.txt", header = TRUE) > attach(peregrine) 以下のオブジェクトは peregrine (pos = 3) からマスクされています: Eyasses, Pairs, R.Pairs, Year > > # Bundle data (note yet another standardization for year) > win.data <- list(C = R.Pairs, N = Pairs, nyears = length(Pairs), year = (Year-1985)/ 20) > > # Initial values > inits <- function() list(alpha = runif(1, -1, 1), beta1 = runif(1, -1, 1), beta2 = runif(1, -1, 1)) > > # Parameters monitored > params <- c("alpha", "beta1", "beta2", "p") > > # MCMC settings > ni <- 2500 > nt <- 2 > nb <- 500 > nc <- 3 > > # Call WinBUGS from R (BRT < 1 min) > out3 <- bugs(data = win.data, inits = inits, parameters.to.save = params, model.file = "GLM_Binomial.txt", n.chains = nc, n.thin = nt, n.iter = ni, n.burnin = nb, debug = TRUE, bugs.directory = bugs.dir, working.directory = getwd()) > |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 |
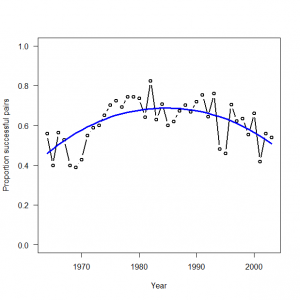
> # Summarize posteriors and plot estimates > print(out3, dig = 3) Inference for Bugs model at "GLM_Binomial.txt", fit using WinBUGS, 3 chains, each with 2500 iterations (first 500 discarded), n.thin = 2 n.sims = 3000 iterations saved mean sd 2.5% 25% 50% 75% 97.5% Rhat n.eff alpha 0.788 0.055 0.684 0.751 0.787 0.826 0.893 1.001 3000 beta1 -0.034 0.071 -0.169 -0.085 -0.034 0.014 0.107 1.002 1400 beta2 -0.893 0.121 -1.133 -0.975 -0.889 -0.814 -0.658 1.002 1600 p[1] 0.460 0.037 0.389 0.435 0.461 0.485 0.532 1.003 870 p[2] 0.482 0.034 0.415 0.459 0.483 0.506 0.548 1.003 880 p[3] 0.504 0.031 0.442 0.482 0.504 0.525 0.564 1.003 890 p[4] 0.524 0.029 0.466 0.504 0.524 0.544 0.580 1.003 920 p[5] 0.543 0.026 0.491 0.525 0.542 0.561 0.594 1.003 960 p[6] 0.561 0.024 0.513 0.544 0.560 0.578 0.608 1.002 1000 p[7] 0.577 0.022 0.533 0.562 0.577 0.593 0.620 1.002 1100 p[8] 0.592 0.020 0.553 0.579 0.592 0.607 0.632 1.002 1200 p[9] 0.606 0.019 0.570 0.594 0.606 0.619 0.643 1.002 1400 p[10] 0.619 0.017 0.585 0.608 0.619 0.631 0.653 1.002 1600 p[11] 0.631 0.016 0.599 0.620 0.631 0.642 0.663 1.001 2000 p[12] 0.641 0.015 0.611 0.631 0.641 0.652 0.672 1.001 2700 p[13] 0.651 0.014 0.622 0.641 0.651 0.660 0.679 1.001 3000 p[14] 0.659 0.014 0.631 0.650 0.659 0.668 0.686 1.001 3000 p[15] 0.666 0.013 0.640 0.657 0.666 0.675 0.692 1.001 3000 p[16] 0.672 0.013 0.647 0.663 0.672 0.680 0.697 1.001 3000 p[17] 0.677 0.013 0.653 0.669 0.677 0.686 0.702 1.001 3000 p[18] 0.681 0.012 0.657 0.673 0.681 0.690 0.705 1.001 3000 p[19] 0.684 0.012 0.660 0.676 0.684 0.692 0.708 1.001 3000 p[20] 0.686 0.012 0.663 0.678 0.686 0.694 0.709 1.001 3000 p[21] 0.687 0.012 0.664 0.679 0.687 0.695 0.710 1.001 3000 p[22] 0.687 0.012 0.665 0.679 0.687 0.696 0.710 1.001 3000 p[23] 0.686 0.011 0.664 0.679 0.686 0.694 0.708 1.001 3000 p[24] 0.685 0.011 0.663 0.677 0.685 0.692 0.706 1.001 3000 p[25] 0.682 0.011 0.660 0.674 0.682 0.689 0.703 1.001 3000 p[26] 0.678 0.011 0.657 0.671 0.678 0.685 0.698 1.001 3000 p[27] 0.673 0.010 0.652 0.666 0.673 0.680 0.693 1.001 3000 p[28] 0.667 0.010 0.647 0.661 0.668 0.674 0.687 1.001 3000 p[29] 0.661 0.010 0.641 0.654 0.661 0.667 0.679 1.001 3000 p[30] 0.653 0.010 0.633 0.646 0.653 0.659 0.671 1.001 3000 p[31] 0.644 0.009 0.625 0.637 0.644 0.650 0.662 1.001 3000 p[32] 0.633 0.009 0.615 0.627 0.634 0.640 0.652 1.001 3000 p[33] 0.622 0.010 0.603 0.616 0.622 0.629 0.640 1.001 3000 p[34] 0.610 0.010 0.590 0.603 0.610 0.616 0.628 1.001 3000 p[35] 0.596 0.011 0.574 0.589 0.596 0.603 0.617 1.001 3000 p[36] 0.581 0.012 0.557 0.573 0.581 0.589 0.604 1.001 3000 p[37] 0.565 0.013 0.538 0.556 0.565 0.574 0.590 1.001 3000 p[38] 0.547 0.015 0.517 0.537 0.547 0.557 0.576 1.000 3000 p[39] 0.528 0.017 0.494 0.517 0.529 0.540 0.561 1.001 3000 p[40] 0.508 0.019 0.470 0.496 0.509 0.521 0.545 1.001 3000 deviance 289.602 2.414 286.800 287.800 289.000 290.800 295.800 1.004 1000 For each parameter, n.eff is a crude measure of effective sample size, and Rhat is the potential scale reduction factor (at convergence, Rhat=1). DIC info (using the rule, pD = Dbar-Dhat) pD = 3.0 and DIC = 292.6 DIC is an estimate of expected predictive error (lower deviance is better). > plot(Year, R.Pairs/Pairs, type = "b", lwd = 2, col = "black", main = "", las = 1, ylab = "Proportion successful pairs", xlab = "Year", ylim = c(0,1)) > lines(Year, out3$mean$p, type = "l", lwd = 3, col = "blue") |
データを覗いてみる。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 |
> data $nyears [1] 40 $alpha [1] 1 $beta1 [1] -0.03 $beta2 [1] -0.9 $year [1] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 [26] 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 $YR [1] -0.95 -0.90 -0.85 -0.80 -0.75 -0.70 -0.65 -0.60 -0.55 -0.50 -0.45 -0.40 [13] -0.35 -0.30 -0.25 -0.20 -0.15 -0.10 -0.05 0.00 0.05 0.10 0.15 0.20 [25] 0.25 0.30 0.35 0.40 0.45 0.50 0.55 0.60 0.65 0.70 0.75 0.80 [37] 0.85 0.90 0.95 1.00 $exp.p [1] 0.5538528 0.5739535 0.5927270 0.6101636 0.6262705 0.6410674 0.6545839 [8] 0.6668562 0.6779245 0.6878313 0.6966192 0.7043294 0.7110009 0.7166694 [15] 0.7213665 0.7251195 0.7279507 0.7298773 0.7309111 0.7310586 0.7303206 [22] 0.7286927 0.7261647 0.7227212 0.7183416 0.7130002 0.7066668 0.6993070 [29] 0.6908829 0.6813537 0.6706773 0.6588110 0.6457135 0.6313470 0.6156796 [36] 0.5986877 0.5803597 0.5606991 0.5397286 0.5174929 $C [1] 29 29 48 18 23 16 19 14 47 33 47 31 26 45 31 21 26 15 42 36 26 69 18 75 68 [26] 21 55 36 33 43 28 21 47 18 45 48 35 18 18 39 $N [1] 61 54 88 31 34 22 31 23 70 52 61 46 39 64 41 31 38 22 57 51 36 92 24 98 94 [26] 30 80 48 53 58 45 34 67 29 83 93 69 32 40 73 |
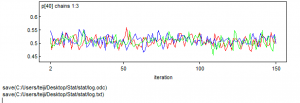
初めのMCMC150ループを見てみる。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
> win.data <- list(C = R.Pairs, N = Pairs, nyears = length(Pairs), year = (Year-1985)/ 20) > > # Initial values > inits <- function() list(alpha = runif(1, -1, 1), beta1 = runif(1, -1, 1), beta2 = runif(1, -1, 1)) > > # Parameters monitored > params <- c("alpha", "beta1", "beta2", "p") > > # MCMC settings > ni <- 150 > nt <- 1 > nb <- 1 > nc <- 3 > > # Call WinBUGS from R (BRT < 1 min) > out4 <- bugs(data = win.data, inits = inits, parameters.to.save = params, model.file = "GLM_Binomial.txt", n.chains = nc, n.thin = nt, n.iter = ni, n.burnin = nb, debug = TRUE, bugs.directory = bugs.dir, working.directory = getwd()) |