Rによるベイズ統計分析(照井伸彦著, 朝倉書店)からの学習ノート
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
5.1 モンテカルロ法
モンテカルロ積分 Monte Carlo integration
θの確率密度をp(θ)とし、θのある関数g(θ)の期待値r = E(g(θ)] = ∫g(θ)p(θ)dθである積分値を、p(θ)からのN個の独立標本{θ(1), θ(2), …,θ(N)}を用いて、大数の法則を利用して求める方法。
この方法の基礎になる分布からの標本の抽出法として、繰り返しシミュレーション法の一つのクラスであるマルコフ連鎖モンテカルロ法(MCMC)がある。
エルゴード性:数多くの施行の繰り返しののちに、最初の状態に関係なく一定の確率状態になる性質
エルゴード性を有するマルコフ連鎖をシミュレートするのがMCMC方法であり、その代表的アルゴリズムとしてギッブスサンプリング(Gibbs sampling)がある。
現代のベイズ統計によるモデリングでは、共役事前分布とMCMC法を上手に組み合わせて、分析対象に対して効率的で柔軟なモデリング技術を提供している。
5.2 モンテカルロ法により積分評価ー非繰返しモンテカルロ法
5.2.1 モンテカルロ積分
θの確率密度をp(θ)とし、p(θ)からのN個の無作為標本{θ(1), θ(2), …,θ(N)}が得られた時、
関数g(θ)の期待値r = E(g(θ)] = ∫g(θ)p(θ)dθ ≒ 1/N Σg(θ(j))を用いて推定する方法
ここで確率変数g(θ(j))が分散Var(g(θ))を持つとすれば、推定値の精度を分散で評価すれば、
Var(r) = 1/N^2 ΣVar(g(θ(j)) = 1/N Var(g(θ)) = 1/N Σ[g(θ(j)-r]^2/(N-1)
5.3.3 連続状態空間への拡張
現在 θ∈Θ の状態から A∈Θ へ推移する確率は、その条件付き確率をp(φ|Θ)dφ とした場合、
K(Θ, A) = ∫ p(φ|Θ)dφ
で、推移カーネル(transitional kernel)と表される。
ここでは、不変式 ∫A π(θ)dθ = ∫φ K(Θ, A)π(θ)dθ
が成り立つ。
可逆性の条件は π(θ)p(φ|θ) = π(φ)p(θ|φ)
5.3.4 ギッブスサンプリング
初期値θ(0)を与件として、{p(θ(i)|θ(i-1)}、すなわちp(θ(1)|θ(0)),θ(2)|θ(1)),…, θ(i)|θ(i-1))のそれぞれから得られるサンプリング列{θ(0),θ(1),….,θ(t)} はマルコフ連鎖である。ギッブスサンプリングは、これを用いて、θ=(θ(0),θ(1),….,θ(k))のk次元分布を評価する方法であり、完全条件付き分布(full conditional distribution)が利用できるアルゴリズムである。
ギッブスサンプリング
1. 初期値{θ1(0),….θk(0)}の設定
2. 繰り返し
[ θ1(1) 〜 h(θ1|θ2(0),….θk(0)}
θ2(1) 〜 h(θ2|θ1(0),θ3|θ1(0),….θk(0)}
….
θk(1) 〜 h(θ2|θ1(0),….θk-1(0)}
]
[
θ1(i) 〜 h(θ1|θ2(i-1),….θk(i-1)}
θ2(i) 〜 h(θ2|θ1(i-1),θ3|θ1(i-1),….θk(i-1)}
….
θk(i) 〜 h(θ2|θ1(i-1),….θk-1(i-1)}
]
3. これをN回繰り返す。
例題)正規母集団から15個の観察値yを得た場合のパラメータ(μ, δ^2)の事後分布をギッブスサンプリングを用いて評価する。
y <- c(1.53, 19.02, 5.34, -2.16, 0.83, 6.74, 5.53,
0.65, -0.49, -0.08, 5.31, 3.18, 7.19, 4.23, 6.45)
特に特徴のない15個の実数。
平均値は、
> mean(y)
[1] 4.218
標準偏差は、
> > sd(y)
[1] 5.051704
分散は、
> var(y)
[1] 25.51972
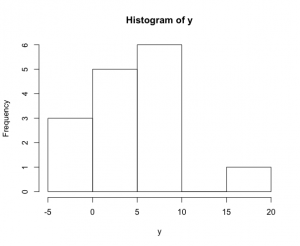
ヒストグラムを描くと
> hist(y)
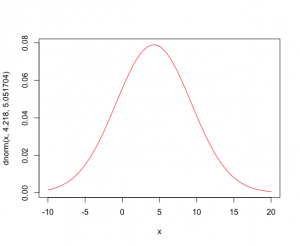
N(4.218,5.051704)を描くと
> curve(dnorm(x,4.218,5.051704),-10,20,col = “red”)
事前分布は、μ〜N(μ0, σ0^2), σ^2 〜IG(r0/2, s0/2)を仮定する。
ギッブスサンプリングのためには、条件付き事後分布p(μ|σ^2, y)およびp(σ^2|μ,y)が必要。
事前分布のパタメータには
μ0=0, σ0^2=100, r0=0.01, s0=100と設定。
### 003 page 59
# Rによる正規母集団のギッブスサンプリング
# Gibbs sampler for non conjugat Normal-Gamma
y <- c(1.53, 19.02, 5.34, -2.16, 0.83, 6.74, 5.53, #15個の観測データ
0.65, -0.49, -0.08, 5.31, 3.18, 7.19, 4.23, 6.45)
my <- mean(y); n <- length(y)
iterations <- 3500 #MCMC繰り返し数設定
m0 <- 0; s0 <- 100; a0 <- 0.01; b0 <- 0.01 #パラメータの初期値設定
theta <- matrix(nrow = iterations, ncol = 2)
cur.mu <- 0; cur.tau <- 1
cur.s <- sqrt(1 / cur.tau)
for (t in 1:iterations){ #3500回のループ
w <- s0 ^ 2 / (cur.s ^ 2 / n + s0 ^ 2)
m <- w * my + (1 - w) * m0
s <- sqrt(w + cur.s ^ 2 / n)
cur.mu <- rnorm(1, m, s)
a <- a0 + 0.5 * n
b <- b0 + 0.5 * sum((y - cur.mu) ^ 2)
cur.tau <- rgamma(1, a, b)
cur.s <- sqrt(1 / cur.tau)
theta[t,] <- c(cur.mu, cur.s) }
op <- par(mfrow = c(2, 1))
p = 1:iterations
plot(p,theta[, 1],type="l",main="mu",xlab=" iteration",
ylab="mu",lty=1,lwd=1)
plot(p,theta[, 2],type="l",main="sigma",xlab=" iteration",
ylab="sigma",lty=1,lwd=1)
par(op)
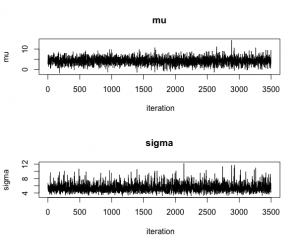
> mean(theta[, 1][501:3500])
[1] 4.198439
> mean(theta[, 2][501:3500])
[1] 5.451327
> sd(theta[, 1][501:3500])
[1] 1.765598
> sd(theta[, 2][501:3500])
[1] 1.148988
> curve(dnorm(x,4.198439,5.451327),-5,20,add = TRUE,col = “green”)
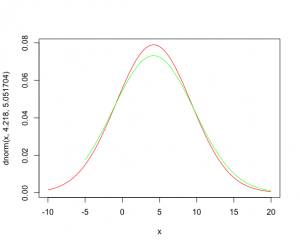
μの分布は
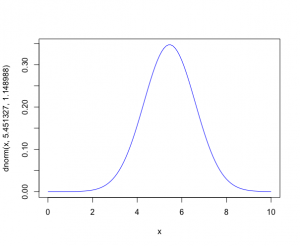
> curve(dnorm(x,5.451327,1.765598),0,10,col = “blue”)
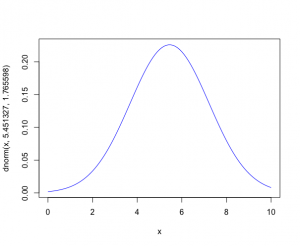
σ^2の分布は
> curve(dnorm(x,5.451327,1.148988),0,10,col = “blue”)