確率と情報の科学:データ解析のための統計モデリング入門:久保拓弥、岩波書店
第10章階層ベイズモデル GLMMのベイズモデル化
より詳細な理解へ
???????????
10.1 例題:個体差と生存種子数(個体差あり)
|
1 2 3 4 5 6 7 8 9 10 |
> d <- read.csv("data7a.csv") > d id y 1 1 0 2 2 2 3 3 7 4 4 8 5 5 1 ...... 100 100 0 |
10.2 GLMMの階層ベイズモデル化
リンク関数と線形予測子を
logit(qi) = β + ri
とする。
切片β, 個体差riは、平均ゼロ標準偏差sの正規分布に従う。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
model { for (i in 1:N) { Y[i] ~ dbin(q[i], 8) #二項分布 logit(q[i]) <- beta + r[i] # 生存確率 } 解説:N個分ので観測データとの対応付け。観測された生存数Y[i]は、生存確率q[i]でサイズ8の二項分布(dbin(q[i]/ 8))に従う。種子の生存率q[i]は線形予測子beta + r[i]とロジットリンク関数logit(q[i])で与えられる。 以下は事前分布の定義 beta ~ dnorm(0, 1.0E-4) # 無情報事前分布>平均値ゼロで標準偏差10^2の正規分布 for (i in 1:N) { r[i] ~ dnorm(0, tau) # 階層事前分布>平均ゼロで標準偏差sの正規分布 } tau <- 1 / (s * s) # tau tauは分散の逆数 s ~ dunif(0, 1.0E+4) # 無情報事前分布>0<s<10^4の一様分布 } |
10.3.2 階層ベイズモデルの事後分布推定と予測
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
> source("R2WBwrapper.R") # reading "R2WBwrapper.R" (written by kubo@ees.hokudai.ac.jp)... > d <- read.csv("data7a.csv") > > clear.data.param() > set.data("N", nrow(d)) > set.data("Y", d$y) > > set.param("beta", 0) > set.param("r", rnorm(N, 0, 0.1)) > set.param("s", 1) > set.param("q", NA) NULL > > post.bugs <- call.bugs( + file = "model.bug.txt", + n.iter = 10100, n.burnin = 100, n.thin = 10 + ) > post.list <- to.list(post.bugs) > post.mcmc <- to.mcmc(post.bugs) |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 |
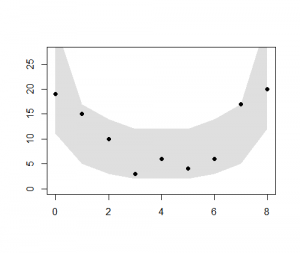
> d <- read.csv("data7a.csv") > library(R2WinBUGS) > if (!exists("post.bugs")) load("post.bugs.RData") > #post.mcmc <- to.mcmc(post.bugs) > post.mcmc <- as.mcmc(post.bugs$sims.matrix) > > q <- sum(d$y) / (8 * nrow(d)) > logistic <- function(z) 1 / (1 + exp(-z)) > n <- nrow(d) > size <- 8 > q <- sum(d$y) / (size * n) > > f.gaussian.binom <- function(alpha, x, size, fixed, sd) + dbinom(x, size, logistic(fixed + alpha)) * dnorm(alpha, 0, sd) > > d.gaussian.binom <- function(v.x, size, fixed, sd) sapply( + v.x, function(x) integrate( + f = f.gaussian.binom, + lower = -sd * 10, + upper = sd * 10, + # for f.gaussian.binom + x = x, + size = size, + fixed = fixed, + sd = sd + )$value + ) > > plot.data <- function() plot( + 0:size, summary(as.factor(d$y)), + ylim = range(c(0, dbinom(0:size, size, q) * n)), + xlab = "", + ylab = "", + pch = 19 + ) > plot.polygon <- function(mm, p) + { + pp <- 1 - p + qp <- apply(mm, 1, quantile, probs = c(0.5 * pp, 1 - 0.5 * pp)) + polygon( + c(0:size, size:0), + c(qp[1,], rev(qp[2,])), + border = NA, + col = "#00000020" + ) + } > > plot.lines <- function(mm) + { + apply( + mm, 2, + function(x) lines(0:size, x, col = "#00000001", lwd = 2) + ) + } > > beta <- post.mcmc[, "beta"] > sigma <- post.mcmc[, "s"] > if (!exists("my")) { + cat("# generating mp ") + mp <- sapply( + 1:nrow(post.mcmc), + function(i) { + if (i %% 100 == 0) cat(".") + d.gaussian.binom( + 0:size, size, + fixed = beta[i], + sd = sigma[i] + ) + } + ) + cat(" done\n") + my <- apply( + mp, 2, function(prob) summary( + factor( + sample(0:size, n, replace = TRUE, prob = prob), + levels = 0:size + ) + ) + ) + } > plot.median <- function() + { + lines( + 0:size, apply(mp * n, 1, median), + type = "b", + col = "black", + bg = "white", + pch = 21 + ) + } > plot.data() > q.env <- apply(my, 1, quantile, probs = c(0.025, 0.975)) > polygon( + c(0:size, size:0), + c(q.env[1,], rev(q.env[2,])), # 0.025 and 0.975 + border = FALSE, + col = "#00000020" + ) |
|
1 |
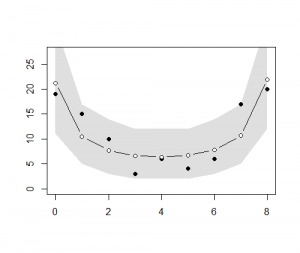
> plot.median() |
10.5 個体差+場所差の階層ベイズモデル
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
model { for (i in 1:N.sample) { Y[i] ~ dpois(lambda[i]) log(lambda[i]) <- beta1 + beta2 * F[i] + r[i] + rp[Pot[i]] } beta1 ~ dnorm(0, 1.0E-4) beta2 ~ dnorm(0, 1.0E-4) for (i in 1:N.sample) { r[i] ~ dnorm(0, tau[1]) } for (j in 1:N.pot) { rp[j] ~ dnorm(0, tau[2]) } for (k in 1:N.tau) { tau[k] <- 1.0 / (s[k] * s[k]) s[k] ~ dunif(0, 1.0E+4) } } |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
> source("R2WBwrapper.R") # reading "R2WBwrapper.R" (written by kubo@ees.hokudai.ac.jp)... > d <- read.csv("d1.csv") > > clear.data.param() > set.data("N.sample", nrow(d)) > set.data("N.pot", length(levels(d$pot))) > set.data("N.tau", 2) > > set.data("Y", d$y) > set.data("F", as.numeric(d$f == "T")) > set.data("Pot", as.numeric(d$pot)) > > set.param("beta1", 0) > set.param("beta2", 0) > set.param("s", c(1, 1)) > set.param("r", rnorm(N.sample, 0, 0.1)) > set.param("rp", rnorm(N.pot, 0, 0.1)) > > post.bugs <- call.bugs( + file = "model.bug.txt", + n.iter = 51000, n.burnin = 1000, n.thin = 50 + ) > post.list <- to.list(post.bugs) > post.mcmc <- to.mcmc(post.bugs) |
|
1 |
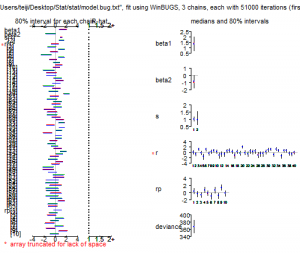
> plot(post.bugs) |
|
1 2 3 |
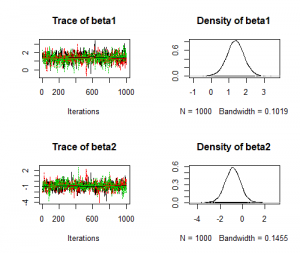
> plot(post.bugs) > s <- colnames(post.mcmc) %in% c("beta1", "beta2") > plot(post.list[,s,]) |