確率と情報の科学：データ解析のための統計モデリング入門：久保拓弥、岩波書店
第10章階層ベイズモデル　GLMMのベイズモデル化
???????????

階層事前分布(hierarchial prior）を使って、一般線形今後モデル（GLMM)を階層ベイズモデル（hierarchial Bayesian model)として扱う方法をまとめる。現実のデータ解析では、個体差だけでなく、調査場所の差などもモデルに含める必要がある。階層ベイズモデルとMCMCサンプリングによるパラメータの推定が威力を発揮する。

10.1 例題：個体差と生存種子数（個体差あり）

> d <- read.csv(“data7a.csv”)
> d
id y
1 1 0
2 2 2
3 3 7
4 4 8
5 5 1
……
100 100 0

> hist(d$y)

10.2 GLMMの階層ベイズモデル化
リンク関数と線形予測子を
logit(qi) = β + ri
とする。
切片β, 個体差riは、平均ゼロ標準偏差sの正規分布に従う。

データが得られる確率p(Y|βi, {ri})=Π(8 yi)qi^yi*(1-qi)^(8-yi)

推定したい事後分布は
　事後分布∝p(Y|β, {ri}) x 事前分布

あとは事前分布を指定すれば統計モデルは完了する。

線形予測子の切片βの事前分布は平均ゼロで、標準偏差100の正規分布を選択する。
p(β）= 1/√(2πX1000^2)exp(-β^2/(2×100^2))

個体差riのパラメータの事前分布は、平均ゼロで標準偏差sの正規分布に従う。

p(ri|s) = 1/√2πs^2(-ri^2/2s^2)

個体差のばらつきsの事前分布はp(s)＝（０から10^4までの連続一様分布）とする。

p(ri|s) は階層事前分布、sは超パラメータ(hyper parameter)、事前分布の事前分布であるp(s)は超事前分布(hyper prior)と呼ぶ。

10.3 階層ベイズモデルの推定・予測
この例題の階層ベイズモデルの事後分布は

p(β,s,{ri}|Y)∝p(Y|β,{ri})p(β)p(s)Πp(ri|s)

10.3.1 階層ベイズモデルのMCMCサンプリング
http://hosho.ees.hokudai.ac.jp/~kubo/stat/iwanamibook/fig/hbm/model.bug.txt

model
{
for (i in 1:N) {
Y[i] ~ dbin(q[i], 8) #二項分布
logit(q[i]) <- beta + r[i] # 生存確率 } 解説：N個分ので観測データとの対応付け。観測された生存数Y[i]は、生存確率q[i]でサイズ8の二項分布(dbin(q[i]/ 8))に従う。種子の生存率q[i]は線形予測子beta + r[i]とロジットリンク関数logit(q[i])で与えられる。 以下は事前分布の定義 beta ~ dnorm(0, 1.0E-4) # 無情報事前分布>平均値ゼロで標準偏差10^2の正規分布
for (i in 1:N) {
r[i] ~ dnorm(0, tau) # 階層事前分布>平均ゼロで標準偏差sの正規分布
}
tau <- 1 / (s * s) # tau tauは分散の逆数 s ~ dunif(0, 1.0E+4) # 無情報事前分布＞010.3.2　階層ベイズモデルの事後分布推定と予測

生存種子数yの確率分布は、二項分布p(y|β,r)と正規分布p(r|s)の無限混合分布であり、以下の式で表せるとする。
p(y|β,s) = ∫p(y|β,r)p(r|s)dr

> source(“R2WBwrapper.R”)
# reading “R2WBwrapper.R” (written by kubo@ees.hokudai.ac.jp)…
> d <- read.csv("data7a.csv") >
> clear.data.param()
> set.data(“N”, nrow(d))
> set.data(“Y”, d$y)
>
> set.param(“beta”, 0)
> set.param(“r”, rnorm(N, 0, 0.1))
> set.param(“s”, 1)
> set.param(“q”, NA)
NULL
>
> post.bugs <- call.bugs( + file = "model.bug.txt", + n.iter = 10100, n.burnin = 100, n.thin = 10 + ) > #post.list <- to.list(post.bugs) > #post.mcmc <- to.mcmc(post.bugs) 以下作図用のRコード http://hosho.ees.hokudai.ac.jp/~kubo/stat/iwanamibook/fig/hbm/fig10_04.R

> d <- read.csv("data7a.csv") > library(R2WinBUGS)
> if (!exists(“post.bugs”)) load(“post.bugs.RData”)
> #post.mcmc <- to.mcmc(post.bugs) > post.mcmc <- as.mcmc(post.bugs$sims.matrix) >
> q <- sum(d$y) / (8 * nrow(d)) > logistic <- function(z) 1 / (1 + exp(-z)) > n <- nrow(d) > size <- 8 > q <- sum(d$y) / (size * n) >
> f.gaussian.binom <- function(alpha, x, size, fixed, sd) + dbinom(x, size, logistic(fixed + alpha)) * dnorm(alpha, 0, sd) >
> d.gaussian.binom <- function(v.x, size, fixed, sd) sapply( + v.x, function(x) integrate( + f = f.gaussian.binom, + lower = -sd * 10, + upper = sd * 10, + # for f.gaussian.binom + x = x, + size = size, + fixed = fixed, + sd = sd + )$value + ) >
> plot.data <- function() plot( + 0:size, summary(as.factor(d$y)), + ylim = range(c(0, dbinom(0:size, size, q) * n)), + xlab = "", + ylab = "", + pch = 19 + ) > plot.polygon <- function(mm, p) + { + pp <- 1 - p + qp <- apply(mm, 1, quantile, probs = c(0.5 * pp, 1 - 0.5 * pp)) + polygon( + c(0:size, size:0), + c(qp[1,], rev(qp[2,])), + border = NA, + col = "#00000020" + ) + } >
> plot.lines <- function(mm) + { + apply( + mm, 2, + function(x) lines(0:size, x, col = "#00000001", lwd = 2) + ) + } >
> beta <- post.mcmc[, "beta"] > sigma <- post.mcmc[, "s"] > if (!exists(“my”)) {
+ cat(“# generating mp “)
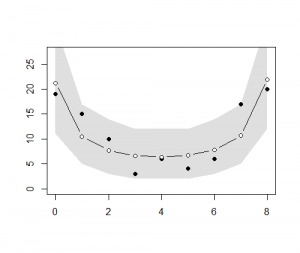
+ mp <- sapply( + 1:nrow(post.mcmc), + function(i) { + if (i %% 100 == 0) cat(".") + d.gaussian.binom( + 0:size, size, + fixed = beta[i], + sd = sigma[i] + ) + } + ) + cat(" done\n") + my <- apply( + mp, 2, function(prob) summary( + factor( + sample(0:size, n, replace = TRUE, prob = prob), + levels = 0:size + ) + ) + ) + } > plot.median <- function() + { + lines( + 0:size, apply(mp * n, 1, median), + type = "b", + col = "black", + bg = "white", + pch = 21 + ) + } > 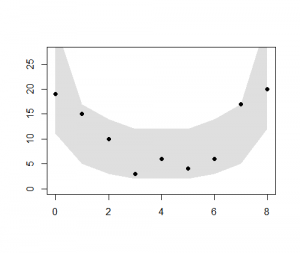plot.data()
> q.env <- apply(my, 1, quantile, probs = c(0.025, 0.975)) > polygon(
+ c(0:size, size:0),
+ c(q.env[1,], rev(q.env[2,])), # 0.025 and 0.975
+ border = FALSE,
+ col = “#00000020”
+ )

> plot.median()

10.4ベイズモデルで使うさまざまな事前分布
ベイズ統計モデルでよく使用される3種類の事前統計分布は(1)主観的な事前分布、(2)無情報事前分布、(3)階層事前分布である。ただし、本書では(1）考え方は取らない。

パラメータの事前分布として、(2)無情報事前分布、(3)階層事前分布のどちらを選択するのか？　その選択は、そのパラメータがデータ全体のどの範囲を説明しているかに依存している。現実的な統計モデルには、以下の２種類のパラメータがある。データ全体を大域的に説明する少数のパラメータ(global)と、データのごく一部だけを説明する局所的な多数のパラメータ)local)とがある。この例では、切片βは、大域的なパラメータであり、無情報事前分布を用いて推定する。一方、個々のriについてはデータの一部を説明しているだけで、無情報事前分布を指定するのではなくて、{ri}全体のばらつきを変えられる階層事前分布を指定する。

10.5 個体差＋場所差の階層ベイズモデル

場所差も組み込んだ階層ベイズモデルを説明する。
植木鉢10個に対して、それぞれの鉢に10個の植物が植えられている。
j∈{A,B,C,D,E}の植木鉢は無処理(fi=0)で、j∈{F,G,H,I,J}は施肥処理(fi=1).

個体差と植木鉢差を同時に扱う統計モデルを作る。
これまで同様に個体iの種子数yiのばらつきを平均λiのポアソン分布
p(yi|λi) = λi^yiexp(-λi)/yi!

線形予測子と対数リンク関数を使って、平均種子数λiは、
logλi = β1 + β2fi + ri + rj(i)

β1: 切片
β2: 施肥処理の有無を表すfiの係数
ri: 個体iの効果
植木鉢jの効果rj(i)

個体を表すriは100、ばらつきをS
植木鉢の差であるrj(i)は10個、ばらつきをSp

大域的な平均パラメータのβ1とβ2には、無情報事前分布、平均ゼロの押しつぶされた正規分布。
大域的なばらつきパラメータであるSとSpは無情報事前分布から、ゼロから10^4の範囲を取る一様分布。
局所パラメータであるriとrj(i)は階層事前分布、平均ゼロで恭順偏差はそれぞれSとSp

この統計モデルのBUGSコードは以下の通り。
http://hosho.ees.hokudai.ac.jp/~kubo/stat/iwanamibook/fig/hbm/nested/model.bug.txt
model
{
for (i in 1:N.sample) {
Y[i] ~ dpois(lambda[i])
log(lambda[i]) <- beta1 + beta2 * F[i] + r[i] + rp[Pot[i]] } beta1 ~ dnorm(0, 1.0E-4) beta2 ~ dnorm(0, 1.0E-4) for (i in 1:N.sample) { r[i] ~ dnorm(0, tau[1]) } for (j in 1:N.pot) { rp[j] ~ dnorm(0, tau[2]) } for (k in 1:N.tau) { tau[k] <- 1.0 / (s[k] * s[k]) s[k] ~ dunif(0, 1.0E+4) } } 施肥処理の有無を表す因子型の説明をF[i]＞Rのコード内で、無処理の個体ではデータF[i]をゼロ、施肥処理の個体では、F[i]を1とする。 あと、植木鉢差rp[Pot[i]]は、植木鉢の名前{A,B,....J}を整数{1,2,....10}とし、rp[j]が植木鉢の効果rj(i)。個体iのいる植木鉢の番号をあらわすPot[i]はiが5であれば１、iが33であれば4となるようなデータであり、Rの中でPotの値を指定する。 > source(“R2WBwrapper.R”)
# reading “R2WBwrapper.R” (written by kubo@ees.hokudai.ac.jp)…
> d <- read.csv("d1.csv") >
> clear.data.param()
> set.data(“N.sample”, nrow(d))
> set.data(“N.pot”, length(levels(d$pot)))
> set.data(“N.tau”, 2)
>
> set.data(“Y”, d$y)
> set.data(“F”, as.numeric(d$f == “T”))
> set.data(“Pot”, as.numeric(d$pot))
>
> set.param(“beta1”, 0)
> set.param(“beta2”, 0)
> set.param(“s”, c(1, 1))
> set.param(“r”, rnorm(N.sample, 0, 0.1))
> set.param(“rp”, rnorm(N.pot, 0, 0.1))
>
> post.bugs <- call.bugs( + file = "model.bug.txt", + n.iter = 51000, n.burnin = 1000, n.thin = 50 + ) > post.list <- to.list(post.bugs) > post.mcmc <- to.mcmc(post.bugs) > plot(post.bugs)

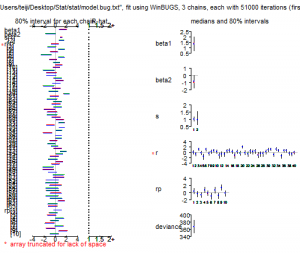
> plot(post.bugs)
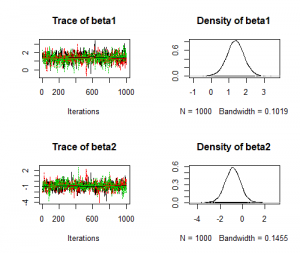
> s <- colnames(post.mcmc) %in% c("beta1", "beta2") > plot(post.list[,s,])

10.6 この章のまとめ
GLMMをベイズモデル化すると階層ベイズモデルになる。
階層ベイズモデルとは、事前分布となる確率分布のパラメータにも事前分布が指定されている統計モデルである。
無情報事前分布と階層事前分布をつかうことで、ベイズ統計モデルから主観的な事前分布を排除できる。
個体差＋場所差といった複雑な構造のあるデータの統計モデリングでは、階層ベイズモデルとMCMCサンプリングによるパラメータ推定の組み合わせで対処する。

参考までにR自体にも、MCMCサンプリングで推定できるMCMCglmmパッケージがある。