確率と情報の科学:データ解析のための統計モデリング入門:久保拓弥、岩波書店
第9章GLMのベイズモデル化と事後分布の推定
——————————–
WinBUGSのインストレーション、環境設定を含む下準備
ベイズ統計の大海原を彷徨い、理解できた点、いまだ全く解らない点など、モヤッとした状態が続く。
知識の整理を計るため、統計学の成書としての本書の章を精読する。ついては、WinBUGSをインストールする必要がある。WinBUGS とは、1989 年にケンブリッジ大学のMRC Biostatistics Unit において開発が始められたBUGS(Bayesian inference Using Gibbs Sampling)というソフトウェアのMS-Windows版であり、マルコフ連鎖モンテカルロ(Markov chain Monte Carlo; MCMC)法によりベイズ階層モデルの解析を行うソフトウェアのことである。
当然、WinBUGSは、Windows版なので、Mac OS Xでは作動しないし、Mac版もない。従って、Macでの使用は、MacOSXにインストールしたVirtual Boxか、VMware Fusion内で動かすWindows 10で使用するとした。
VMware Fusion ver 7をver 10にまずアップグレードした。 続いて、USB付きのWinodows 10を仮想環境に載せることとした。このUSBキーからWindows 10をVMwareの仮想環境にインストールするのにまたすったもんだだった。このUSBインストールは、Unified Extensible Firmware Interface (ユニファイド・エクステンシブル・ファームウェア・インタフェース)という、OSとファームウエア間をやり取りするインターフェースの仕様で、BIOSが行っていたことを、UEFIが替わって行うという仕組みらしい。以下のサイトを参考にして、USBキーからWindows 10をなんとか完了した。ただし、Fusion 10では、すでにfirmware = “efi”等が“(仮想マシンの名前).vmx” というファイルには記載済であったりして、余計に混乱した。
https://medium.com/@_myoshida/vmware-fusion-8-に-usb-メモリから-windows-10-をインストールする-ae49fec52d95
WInBUGSは、以下のサイトからWinBUGS 1.4がダウンロードできる。
https://www.mrc-bsu.cam.ac.uk/software/bugs/the-bugs-project-winbugs/
同じく、サイトからテキストファイルpatch for 1.4.3をダウンロードして、patch内の以下の記述に従って、WinBUGS>Tools>Decode>Decode Allでver.1.4.3に更新する。
WinBUGS Cumulative Patch No. 3 (Version 1.4.3), August 6, 2007
1. Start your copy of WinBUGS 1.4 and open this file from within it.
2. Select “Decode” from the “Tools” menu — the “Decode” dialogue box
should appear.
3. Click on the “Decode All” button to install the upgrade patch. You
may be prompted to create two new directories during the installation
process — click on “OK” for each one.
4. Quit WinBUGS to complete the installation. (You may delete this file
afterwards if you wish.)
5. After installation, the front page of the WinBUGS manual (F1) should
provide a hyperlink to a list of upgraded/new features.
もう一点、本書の精読に必要となるWinBUGSの使用に関して注意が必要なことは、Windows10にインストールした、RとRstudioとWinBUGSは管理者権限で動かさないと、色々と「書き込み出来ない」等のエラーがでてしまうことである。管理者権限での作動は、exeファイルを右クリック(マックではコントロールキーを押しながらクリック)して、ファイルのプロパティーを出して、「互換性」タブを開いて、下の方にあるチェックボックス「管理者としてこのプログラムを実行する」にチェックを入れておくことで完了する。
同書の著者の以下のサポートサイトの該当部分を参照しながら、ソフトウェアを実際に動かしながら、読み進まないと理解が難しい。
http://hosho.ees.hokudai.ac.jp/~kubo/ce/IwanamiBook.html
9.1 例題:種子数のポアソン回帰(個体差なし)
架空の植物個体iでは体サイズxiに依存して、種子数yiの平均が増減する。ここでの架空植物の個体数は20。
まずはデータファイルd.RDataを以下のサイトからダウンロードして、RStudioのプロジェクトフォルダ内に移す。
http://hosho.ees.hokudai.ac.jp/~kubo/ce/IwanamiBook.html
次にRSTudioから、データファイルを指定して、データを変数dに移す。
> load(“d.RData”)
> d
x y
1 3.000000 5
2 3.210526 3
3 3.421053 6
4 3.631579 7
5 3.842105 7
6 4.052632 5
7 4.263158 9
8 4.473684 9
9 4.684211 7
10 4.894737 10
11 5.105263 12
12 5.315789 8
13 5.526316 7
14 5.736842 4
15 5.947368 4
16 6.157895 11
17 6.368421 9
18 6.578947 9
19 6.789474 8
20 7.000000 6
xが体サイズで、yが種子数。観測データを図にしてみる。
> plot(d$x, d$y)
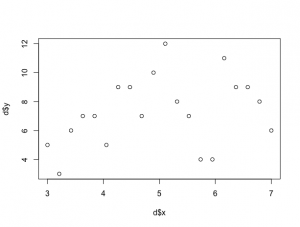
次に、glm()関数を使って、切片、傾き、最尤推定値を求める。
> glm(y~x, family = poisson, data=d)
Call: glm(formula = y ~ x, family = poisson, data = d)
Coefficients:
(Intercept) x
1.56606 0.08334
Degrees of Freedom: 19 Total (i.e. Null); 18 Residual
Null Deviance: 15.66
Residual Deviance: 14.17 AIC: 94.04
その結果、傾き0.08334≒0.1、y切片1.56606≒1.5が得られた。
平均値 λ=exp(1.5+0.1x)
> plot(d$x, d$y)
> result <- lm(exp(1.5+0.1*d$x) ~ x, data = d)
> abline(result)
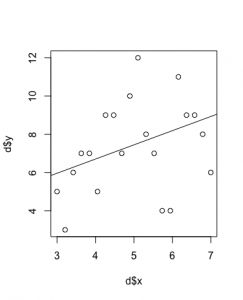
9.2 GLMのベイズモデル化
個体 i の種子数 yi のばらつきは、平均 λi のポアソン分布 p(yi|λi) に従うとする。
線形予測子と対数リンク関数を使って、平均をλi = exp(β1 + β2xi)と指定する。
L(β1, β2) = Πp(yi|λi) = Πp(yi|β1,β2,xi)
X={xi}として、この尤度関数は、iで規程される離散確率分布なので、パラメーター{β1,β2}がある値を取っている時に
Yが得られる確率はp(Y|β1, β2) =L(β1, β2)
ベイズモデルでの事後分布は、(尤度)x(事前分布)に比例するので、
p(β1, β2|Y) ∝?p(Y|β1, β2)p(β1)p(β2)
つまりp(β1, β2|Y)は、事後分布であり、データYが与えられたときのパラメーター{β1,β2}の同時確率である。
p(β1)とp(β2)は、それぞれ切片β1と傾きβ2の事前分布であり、これら事前分布を適切に指定すればベイズモデル化したGLMとなる。
9.3 無情報事前分布
事前分布p(β*)とは、「観測値Yが得られていないときのパラメータβ*の確率分布」>そんなことはわからないので、無情報事前分布(non-informative prior)として、線形予測子β*の値は[-∞,∞]の範囲内で適当な値を取ってよいとなる。ここでは、無限区間(たとえば-109<β*<109の一様分布もありえるが、平均ゼロで標準偏差が大きい平べったい正規分布N(0,100)を採用する。
9.4 ベイズ統計モデルの事後分布の推定
p(β1, β2|Y)をMCMCサンプリングを使って推定する。ここではWinBUGSを使ってベイズ統計モデルをBUGS言語で書かれたBUGSコードで定義する。
9.4.1 ベイズ統計モデルのコーディング
ベイズモデル化したGLMをBUGSコードで表現する。まずは、WinBUGSにBUGSコードを渡すためのテキストを以下のように作成する。
|
1 2 3 4 5 6 7 8 9 10 |
model { Tau.noninformative <- 1.0E-4 for (i in 1:N) { Y[i] ~ dpois(lambda[i]) log(lambda[i]) <- beta1 + beta2 * (X[i] - Mean.X) } beta1 ~ dnorm(0, Tau.noninformative) beta2 ~ dnorm(0, Tau.noninformative) } |
この中身について以下解読する。
全体をmodel{….}でくくって、内部が統計モデルの記述となる。
for (i in 1:N) {….}で囲まれたブロックでは、個体 i=1から20までが
Y[i] ~ dpois(lambda[i])
log(lambda[i]) <- beta1 + beta2 * (X[i] – Mean.X)
に挿入されて、
Y[1] ~ dpois(lambda[1])
log(lambda[1) <- beta1 + beta2 * (X[1] – Mean.X)
Y[2] ~ dpois(lambda[2])
log(lambda[2) <- beta1 + beta2 * (X[2] – Mean.X)
……
Y[20] ~ dpois(lambda[20])
log(lambda[20) <- beta1 + beta2 * (X[20] – Mean.X)
となる。
for{}ブロック内の一行目
Y[i] ~ dpois(lambda[i])
は、個体iの種子数Y[i]が平均lambda[i]のポアソン分布dpois(lambda[i])に従っていることを意味している。
二行目
log(lambda[i]) <- beta1 + beta2 * (X[i] – Mean.X)
は、個体iの平均種子数lambda[i]の指定には対数リンク関数を使用し、さらに右片のその線形予測子ではbeta1とbeta2はそれぞれ切片β1と傾きβ2, X[i]は?明変数である個体iのサイズxi, Mean.Xはxiの標本平均。xiから標本平均を差し引くのは中央化(centralization)をするため(計算の高速化のためであり、中央化自体は結果に影響しない)。
以下で、パラメータβ1, β2の事前分布p(β1)、p(β2)を無情報事前分布に指定する。
beta1 ~ dnorm(0, Tau.noninformative)
beta2 ~ dnorm(0, Tau.noninformative)
関数dnorm(mean, tau)では、meanは平均、tauは分散の逆数を指定するので、標準偏差は1/√tauとなる。
9.4.2 事後分布推定の準備
WinBUGSで事後分布を推定するためには、上記のように統計モデルをBUGSコードで記述する以外に、モデルの中で使用するデータやパラメータの初期値、サンプリング回数などを指定する必要がある。
方法として、WinBUGSに装備されたGUIを使う方法がある(使いにくいとのこと)。
ただし、Rを使用してWinBUGSを以下の手順で操作することもできる。
(1) R内で推定に必要なデータを準備
(2) R内で推定するパラメータの初期値を指定
(3) RからWInBUGSを呼び出して、データ、初期値、MCMC散布ロング回数やBUGSコードファイル名を伝達
(4) Rの指示通りに、WinBUGSがMCMCサンプリングを行う
(5) MCMCサンプリングが終了すればWinBUGSが結果をRに転送する。
(6) MCMCサンプリングの結果をR内で調べる。
R内からWinBUGSを使うためには、RのパッケージR2WinBUGSを使う。ただし、R2WinBUGSもそのままでは使いにくいため、R2WBwrapper.Rファイルで定義したラッパー関数を以下のように使う。
> library(“R2WinBUGS”)
要求されたペッケージ codaをロード中です
要求されたペッケージ bootをロード中です
> source(“R2WBwrapper.R”) #ラッパー関数の読み込み(
R2WBwrapper.Rは、ここhttp://hosho.ees.hokudai.ac.jp/~kubo/ce/r/R2WBwrapper.R
なぜかファイルをRstudioフォルダに置いても読み込めないので、直接貼り付けて実行した。ウィンドウズのファイル名表示で登録拡張子表示をしないでふぁおると設定だと、勝手に.txtが拡張子に付記されても気が付かないことが原因ー>ウィンドウズシステムツール>コントロールパネルー>デスクトップのカスタマイズ>エキスプローラーのオプション>表示>「登録されている拡張子は表示しない」のチェックボックスを外すこと。
https://121ware.com/qasearch/1007/app/servlet/relatedqa?QID=017779
> load(“d.RData”) #データの読み込み
> clear.data.param() #データm初期値設定の準備
#データの設定
set.data(“N”, nrow(d)) #サンプルサイズ
set.data(“Y”, d$y) #応答変数:種子数Y[i]
set.data(“X”, d$x) #?明変数:植物の体サイズxi
set.data(“Mean.X”, mean(s$x)) #X[i]の標本平均
#パラメータの初期値設定
set.param(“beta1”, 0)
set.param(“beta2”, 0)
#WinBUGSを呼び出し、サンプリング結果をpost.bugsに格納
post.bugs <- call.bugs( #call.bugs()関数でWinBUGSを呼び出している。
file = “model.bug.txt”, #ベイズ統計モデルをBUGSコードで書いたテキストファイルを指定
n.iter = 1600, # MCMCサンプリング回数
n.burnin = 100, #MCMCサンプリングのburn-in初期捨て回数
n.thin = 3 #MCMC2つ飛ばしで、3つめごとにデータを「まびき」して取得(サンプルの分量を減らせる)
)
9.4.3 どれだけ長くMCMCサンプリングすればよいのか?
得られた結果を見ながら試行錯誤を繰り返すことになるが、以下の点を注意する。
とくにn.chainsオプションを指定するとMCMCサンプリングの反復回数を指定できる(デフォルトは3)
反復毎のMCMCサンプリングをサンプル列Chainと呼んでいる。複数のサンプル列を比較することにより,
burn-inの区間の長さやモデルの妥当性などが理解できる。サンプル列の解離の大小を調べることを収束診断(convergence assessment)と呼ぶ。
収束しているかどうかの診断では、R指数が用いられる。
R=√(var+/W): Wはサンプル列ごとの分散の平均、var+は周辺事後分布の分散
var+=(n-1)/n*W+1/n*B: ?Bはサンプル列間の分散
この推定値が1.0に近ければ、サンプル列間よりも列内のばらつきが大きいので、収束しているとみなせる。
一方、R>1.1となるようなときには、サンプル列間のばらつきが大きいため定常分布・事後分布は推定できないと判断する。
b.burninや、n.thin, n.iterを調整しても収束しなければ、
不適切な統計モデリング
BUGSコードの間違い
データの間違い
パラメータの初期値があまりにも不適切
などの理由が考えられる。
9. 5 MCMCサンプリングから事後分布を推定
WinBUGSを使ったMCMCサンプリングの結果は、post.bugsに格納される。
post.bugsに格納された情報を取り出して図示する。
わかりやすく図に示すために、post.bugsをmcmcクラスを変換する。
> plot(post.bugs)
> plot(post.bugs)
> post.list <- to.list(post.bugs) > post.mcmc <- to.mcmc(post.bugs) > s <- colnames(post.mcmc) %in% c(“beta1”, “beta2”) > plot(post.list[,s,])
R2WBwrapper.Rファイルで定義されているto.list()関数とto.mcmc()関数を用いて、post.bugsオブジェクトをそれぞれto.listクラスとmcmcクラスのオブジェクトに変換する。
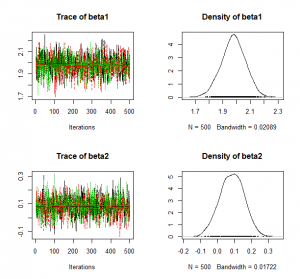
サンプリング過程を示す左図は、それぞれ3本のサンプル列を表示している。
サンプル列間に乖離はない。Rもほぼ1となっている。
右図にしめされるものは、合計1500のサンプルから推定されたβ1とβ2のそれぞれの周辺事後分布(marginal posterior distribution)である。
同時分布である事後分布p(β1,β2,|Y)において、β2で積分すればβ1の周辺事後分布p(β1|Y)=∫p(β1,β2,|Y)dβ2が得られる。
mcmcオブジェクトには、サンプル列の区別なく、β1とβ2の長さ1500のMCMCサンプルを単なる行列として格納している。このpost.mcmcを使って作図できる。
#post.mcmc <- to.mcmc(post.bugs)
post.mcmc <- as.mcmc(post.bugs$sims.matrix)
beta1 <- post.mcmc[, “beta1”]
beta2 <- post.mcmc[, “beta2”]
add.mean <- function(bb1, bb2, lty = 2, lwd = 1, …)
{
lines(d$x, exp(bb1 + bb2 * (d$x – mean(d$x))), lty = lty, lwd = lwd, …)
}
# fig09_06 (A)
par(ask = TRUE)
plot(d$x, d$y, type = “n”, xlab = “x_i”, ylab = “y_i”)
for (i in 1:nrow(post.mcmc)) {
add.mean(beta1[i], beta2[i], lty = 1, col = “#00000004”)
}
points(d$x, d$y)
add.mean(median(beta1), median(beta2), lty = 1, lwd = 2)
http://hosho.ees.hokudai.ac.jp/~kubo/stat/iwanamibook/fig/gibbs/winbugs/fig09_06.R
# fig09_06 (B)
plot(
as.matrix(post.mcmc)[,c(“beta1”, “beta2”)],
lty = 1, col = “#00000030”,
pch = 16, cex = 2,
xlab = “”, ylab = “”
)

9.5.1 事後分布の統計量
WinBUGSで得られたMCMCサンプリングの結果の詳細について、post.bugsに格納されている情報をprint()関数で出力させる。
> print(post.bugs, digits.summary = 3)
Inference for Bugs model at “C:/Users/teiji/Desktop/Stat/stat/model.bug.txt”, fit using WinBUGS,
3 chains, each with 1600 iterations (first 100 discarded), n.thin = 3
n.sims = 1500 iterations saved
mean sd 2.5% 25% 50% 75% 97.5% Rhat n.eff
beta1 1.977 0.085 1.808 1.921 1.978 2.035 2.136 1.003 600
beta2 0.085 0.070 -0.053 0.037 0.088 0.135 0.219 1.001 1500
deviance 92.138 2.035 90.095 90.710 91.475 92.940 97.525 1.000 1500
For each parameter, n.eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor (at convergence, Rhat=1).
DIC info (using the rule, pD = Dbar-Dhat)
pD = 2.1 and DIC = 94.2
DIC is an estimate of expected predictive error (lower deviance is better).
このように表形式で行ごとに、パラメータの平均、標準偏差や分散の分位点や収束の良さを表す指標が示される。
結果、パラメータβ1の事後分布の平均1.973で、中央値は1.975、95%信用区間(
credible interval)は1.805から2.143である。
パラメータβ2の事後分布の95%信頼区間は-0.050から0.209となる。
事後分布の95%信用区間を推定したいのであれば、上下に2,5%に十分な個数のMCMC
サンプルが入る必要があり、合計サンプリング数1500の結果から、95%区間は1425個、区間外には75個のサンプルがあり、少なくともこれくらいは必要。
あと、β2>0となる確率は0.89と考えられた。
Rは、Rhat列に示され、n.effは有効なサンプルサイズ数(number of effective samples)。
9.6 複数パラメータのMCMCサンプリング
上記例に示される複数のパラメータ(例えばβ1とβ2)があるような事後分布からMCMCサンプリングするためには、β1とβ2を交互に更新する方法を用いる。
1) 一旦は、β2を定数だとみなしてβ1を変更
2) 変更されたβ1を定数とみなしてβ2を変更
を繰り返して,p(β1,β2|Y)からのランダムサンプルを発生させる。
9.6.1 ギブスサンプリング
MCMCサンプリングの用いるアルゴリズムの中で、効率と汎用性の点でとくに重要であるのはギブスサンプリング(Gibs sampling)である。メトロポリス法との違いは、更新の方法にある。メトロポリス法ではm「新しい値の候補をあげ、それに変化するかどうかを決める」が、ギブスサンプリングでは、「新しい値の確率分布を作り、その確率分布のランダムサンプルを新しい値とする」。
ここでの新しい確率分布は、多変量確率分布からひとつの変量を除いて、他の変量をすべて定数とする一変量確率分布である。これを全条件つき分布(full conditional distribution, FCD)という。
ギブスサンプリングの手順は
1) 最初に何らかの{β1, β2}の初期値を設定する。
2) p(β1|Y, β2)にしたがう乱数を発生させて、それを新しいβ1とする。
3) p(β2|Y, β1)にしたがう乱数を発生させて、それを新しいβ1とする。
4) このMCMCステップにおけるβ1とβ2を記録しておく
5) 十分な個数のβ1、β2が得られるまで1)-4)を繰り返す。
ギブスサンプリングの利点は、各MCMCステップにおいて、もとの値と更新された値の相関がより少ないことと、MCMCサンプリングの詳細を指定する必要がないことである。
9.6.2 WinBUGSの挙動
WinBUGSがどのようにFCDに従う乱数を発生しているのかは不明であるが、
最初にパラメータβ*の事前分布p(β*)が尤度に比例する確率分布p(Y|β*)の共役事前分布かどうかを調べて、そうであるならば、それらに対応した乱数発生方法を採用する。一方、そうでない場合は、数値的な方法による対処を行って乱数を発生させる。
9.7 まとめ
1. 全個体に共通のパラメータの事前分布として、無情報事前分布を指定する。
2. MCMCサンプリングソフトウェアWInBUGSを使うため、BUGS言語でベイズ統計モデル化したGLMを記述する。
3. WInBUGSにBUGSコードを与えて、MCMCサンプリングを行い、Rを使って事後分布の統計量の分散やMCMCサンプル列の収束診断を行う。
4. MCMCアルゴリズムのなかで、ギブスサンプリングは効率の良い方法の一つである

