????????????
ベイズ推論による機械学習入門 須山 敦志 著 を読む
????????????
NMF:nonnegative matrix factorization
????????????
From demo_nonconjugate.jlからで、取り込むモジュールは無いので、シンプルに入力、実行。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
using PyPlot, PyCall using Distributions import StatsFuns.logsumexp PyDict(matplotlib["rcParams"])["mathtext.fontset"] = "cm" PyDict(matplotlib["rcParams"])["mathtext.rm"] = "serif" PyDict(matplotlib["rcParams"])["lines.linewidth"] = 1.5 PyDict(matplotlib["rcParams"])["font.family"] = "TakaoPGothic" <pre> Out: "TakaoPGothic" <pre> function expt(a, b, sigma, Y, X, N_s) S = rand(Gamma(a, 1.0/b), N_s) C = mean([exp(sum(logpdf.(Normal(s, sigma), Y))) for s in S]) curve = [exp(sum(logpdf.(Normal(mu, sigma), Y))) * pdf(Gamma(a, 1.0/b), mu) for mu in X] m = mean([s*exp(sum(logpdf.(Normal(s, sigma), Y)))/C for s in S]) v = mean([(s-m)^2 * exp(sum(logpdf.(Normal(s, sigma), Y)))/C for s in S]) return curve/C, m, v end |
Out:expt (generic function with 1 method)
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
X = linspace(-5, 10, 1000) a = 2.0 b = 2.0 mu = 1.0 sigma=1.0 # data N = 10 Y = rand(Normal(mu, sigma), N) # calc posterior N_s = 100000 posterior, m, v = expt(a, b, sigma, Y, X, N_s) a_h = m^2 / v b_h = m / v |
Out: 12.311196813709383
|
1 2 3 4 5 6 7 8 9 10 |
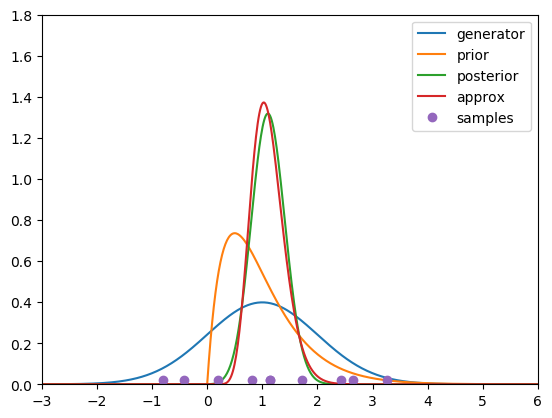
figure() plot(X, pdf(Normal(mu,sigma), X)) plot(X, pdf(Gamma(a,1.0/b), X)) plot(X, posterior) plot(X, pdf(Gamma(a_h,1.0/b_h), X)) plot(Y, 0.02*ones(N), "o") legend(["generator", "prior", "posterior", "approx", "samples"]) #legend(["データ生成分布", "事前分布", "事後分布", "近似分布", "データ"], fontsize=12) xlim([-3, 6]) ylim([0, 1.8]) |