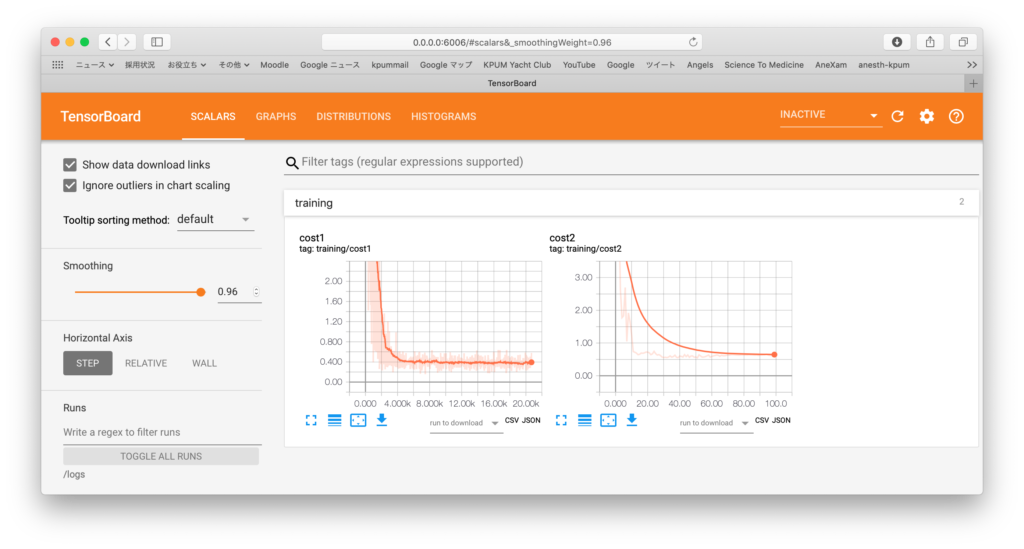
実データで調整してみる。以前の過去の全身麻酔1万3852症例のデータベースから、術中尿量が理想体重あたりで算定される膀胱容量を越えてしまうかどうか、つまり二値分類(Binary Classification)を、事前に得られる術前情報からMulti-Layer Perceptronで推移する。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 |
import tensorflow as tf import numpy as np import pandas as pd from sklearn.model_selection import train_test_split #データファイルからのデータ読み込みとコラム(フィールド名登録) filename = "urecath5R.csv" df = pd.read_csv(filename,encoding="UTF-8",skiprows=1) df.columns = ["id","dept","age","gender","height","weight","ASA","disease","surgery","portion","anesth","position","pre_ope_time","ope_entry_time","anesth_time","surgery_time","bleeding","urine","urecath_neg", "urecath_posi", "predicted_vol", "over", "over_nega"] X_cols = ["dept","age","gender","height","weight","ASA","portion","anesth","position","pre_ope_time"] y_cols = ["over", "over_nega"] X = df[X_cols].values.astype('float') Y = df[y_cols].values.astype('float') X, X_test, Y, Y_test = train_test_split(X, Y) len(X), len(X_test) # パラメータ learning_rate = 0.01 training_epochs = 100 batch_size = 50 display_step = 1 # ネットワークパラメータ n_hidden_1 = 10 # 第1層ニューロン数 n_hidden_2 = 10 # 第2層ニューロン数 n_hidden_3 = 10 # 第3層ニューロン数 n_input = 10 # 入力層数 n_classes = 2 # 出力層数 # プレースホルダー x = tf.placeholder("float", [None, n_input]) y = tf.placeholder("float", [None, n_classes]) # モデルレイヤー with tf.name_scope('layers') as scope: def multilayer_perceptron(x, weights, biases): # 第1隠れ層 RELU活性 layer_1 = tf.add(tf.matmul(x, weights['h1']), biases['b1']) layer_1 = tf.nn.relu(layer_1) # 第2隠れ層 RELU活性 layer_2 = tf.add(tf.matmul(layer_1, weights['h2']), biases['b2']) layer_2 = tf.nn.relu(layer_2) # 第3隠れ層 RELU活性 layer_3 = tf.add(tf.matmul(layer_2, weights['h3']), biases['b3']) layer_3 = tf.nn.relu(layer_3) # 出力層 直線活性化関数 out_layer = tf.matmul(layer_2, weights['out']) + biases['out'] return out_layer # 重み係数、バイアス係数 with tf.name_scope('interface') as scope: step_var = tf.Variable(0, trainable=False) weights = { 'h1': tf.Variable(tf.random_normal([n_input, n_hidden_1])), 'h2': tf.Variable(tf.random_normal([n_hidden_1, n_hidden_2])), 'h3': tf.Variable(tf.random_normal([n_hidden_2, n_hidden_3])), 'out': tf.Variable(tf.random_normal([n_hidden_3, n_classes])) } biases = { 'b1': tf.Variable(tf.random_normal([n_hidden_1])), 'b2': tf.Variable(tf.random_normal([n_hidden_2])), 'b3': tf.Variable(tf.random_normal([n_hidden_3])), 'out': tf.Variable(tf.random_normal([n_classes])) } # モデル生成 with tf.name_scope('model') as scope: pred = multilayer_perceptron(x, weights, biases) w1_log = tf.summary.histogram("w1", weights['h1']) w2_log = tf.summary.histogram("w2", weights['h2']) w3_log = tf.summary.histogram("w3", weights['h3']) w4_log = tf.summary.histogram("w4", weights['out']) # コスト関数、最適化 with tf.name_scope('cost_func') as scope: cost = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits_v2(logits=pred, labels=y)) with tf.name_scope('training') as scope: optimizer = tf.train.AdamOptimizer(learning_rate=learning_rate).minimize(cost, global_step=step_var) cost1_log = tf.summary.scalar("cost1", cost) cost2_log = tf.summary.scalar("cost2", cost) # 変数の初期化 init = tf.global_variables_initializer() # セッション立ち上げ with tf.Session() as sess: writer = tf.summary.FileWriter('./logs', sess.graph) sess.run(init) # 訓練サイクル for epoch in range(training_epochs): avg_cost = 0. total_batch = int(len(X)/batch_size) X_batches = np.array_split(X, total_batch) Y_batches = np.array_split(Y, total_batch) # バッチループ for i in range(total_batch): batch_x, batch_y = X_batches[i], Y_batches[i] step = sess.run(step_var) # バックプロパゲーション最適化、コスト関数 _, c, summary_str1, summary_str2, w1_str, w2_str, w3_str, w4_str = sess.run([optimizer, cost, cost1_log, cost2_log, w1_log, w2_log, w3_log, w4_log], feed_dict={x: batch_x, y: batch_y}) # 平均損失算定 avg_cost += c / total_batch writer.add_summary(summary_str1, global_step=step) # エポックごとのログ if epoch % display_step == 0: print("Epoch:", '%04d' % (epoch+1), "cost=", "{:.9f}".format(avg_cost)) writer.add_summary(summary_str2, epoch) writer.add_summary(w1_str, epoch) writer.add_summary(w2_str, epoch) writer.add_summary(w3_str, epoch) writer.add_summary(w4_str, epoch) print("Optimization Finished!") # モデルをテスト correct_prediction = tf.equal(tf.argmax(pred, 1), tf.argmax(y, 1)) # 精度計算 accuracy = tf.reduce_mean(tf.cast(correct_prediction, "float")) print("Accuracy:", accuracy.eval({x: X_test, y: Y_test})) global result result = tf.argmax(pred, 1).eval({x: X_test, y: Y_test}) |
出力は、
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 |
Epoch: 0001 cost= 12.996831196 Epoch: 0002 cost= 5.091527830 Epoch: 0003 cost= 3.630704669 Epoch: 0004 cost= 2.854212336 Epoch: 0005 cost= 2.393571365 Epoch: 0006 cost= 1.830698144 Epoch: 0007 cost= 1.362857197 Epoch: 0008 cost= 1.050749659 Epoch: 0009 cost= 0.966252408 Epoch: 0010 cost= 0.641816053 Epoch: 0011 cost= 0.575847910 Epoch: 0012 cost= 0.646862613 Epoch: 0013 cost= 0.553969320 Epoch: 0014 cost= 0.538633519 Epoch: 0015 cost= 0.479475871 Epoch: 0016 cost= 0.462024585 Epoch: 0017 cost= 0.456832046 Epoch: 0018 cost= 0.426888565 Epoch: 0019 cost= 0.499762091 Epoch: 0020 cost= 0.419082926 Epoch: 0021 cost= 0.427864665 Epoch: 0022 cost= 0.428373863 Epoch: 0023 cost= 0.412366147 Epoch: 0024 cost= 0.401712736 Epoch: 0025 cost= 0.413094043 Epoch: 0026 cost= 0.388587600 Epoch: 0027 cost= 0.383447928 Epoch: 0028 cost= 0.387419000 Epoch: 0029 cost= 0.406776535 Epoch: 0030 cost= 0.397721399 Epoch: 0031 cost= 0.401628481 Epoch: 0032 cost= 0.400971626 Epoch: 0033 cost= 0.398844143 Epoch: 0034 cost= 0.398389086 Epoch: 0035 cost= 0.394291329 Epoch: 0036 cost= 0.389437957 Epoch: 0037 cost= 0.389456655 Epoch: 0038 cost= 0.385598682 Epoch: 0039 cost= 0.387760509 Epoch: 0040 cost= 0.384587679 Epoch: 0041 cost= 0.383797744 Epoch: 0042 cost= 0.381829699 Epoch: 0043 cost= 0.387931142 Epoch: 0044 cost= 0.387112003 Epoch: 0045 cost= 0.382782753 Epoch: 0046 cost= 0.383860344 Epoch: 0047 cost= 0.379619694 Epoch: 0048 cost= 0.388586827 Epoch: 0049 cost= 0.388381903 Epoch: 0050 cost= 0.382281008 Epoch: 0051 cost= 0.385128317 Epoch: 0052 cost= 0.387040275 Epoch: 0053 cost= 0.385443135 Epoch: 0054 cost= 0.382941529 Epoch: 0055 cost= 0.384841349 Epoch: 0056 cost= 0.384800666 Epoch: 0057 cost= 0.384610893 Epoch: 0058 cost= 0.386373968 Epoch: 0059 cost= 0.382560664 Epoch: 0060 cost= 0.385291286 Epoch: 0061 cost= 0.381220501 Epoch: 0062 cost= 0.380056458 Epoch: 0063 cost= 0.380330499 Epoch: 0064 cost= 0.377685405 Epoch: 0065 cost= 0.377175938 Epoch: 0066 cost= 0.377255466 Epoch: 0067 cost= 0.378071358 Epoch: 0068 cost= 0.377867895 Epoch: 0069 cost= 0.378151173 Epoch: 0070 cost= 0.377914684 Epoch: 0071 cost= 0.377473129 Epoch: 0072 cost= 0.377012356 Epoch: 0073 cost= 0.377847183 Epoch: 0074 cost= 0.377925990 Epoch: 0075 cost= 0.376687482 Epoch: 0076 cost= 0.376281331 Epoch: 0077 cost= 0.376274984 Epoch: 0078 cost= 0.375797580 Epoch: 0079 cost= 0.376094406 Epoch: 0080 cost= 0.376045946 Epoch: 0081 cost= 0.375903829 Epoch: 0082 cost= 0.375957008 Epoch: 0083 cost= 0.375765706 Epoch: 0084 cost= 0.375741490 Epoch: 0085 cost= 0.376012515 Epoch: 0086 cost= 0.375937276 Epoch: 0087 cost= 0.376010826 Epoch: 0088 cost= 0.376011515 Epoch: 0089 cost= 0.375758051 Epoch: 0090 cost= 0.375444158 Epoch: 0091 cost= 0.375140219 Epoch: 0092 cost= 0.375584504 Epoch: 0093 cost= 0.376084303 Epoch: 0094 cost= 0.375375519 Epoch: 0095 cost= 0.376103972 Epoch: 0096 cost= 0.375413385 Epoch: 0097 cost= 0.374594815 Epoch: 0098 cost= 0.376522485 Epoch: 0099 cost= 0.375386964 Epoch: 0100 cost= 0.378003579 Optimization Finished! Accuracy: 0.8380017 |
|
1 2 |
len(X)+len(X_test), len(X), len(X_test) 13852, 10389, 3463 |
で、全13852件のデータについて、10389を訓練データ、3463をテスト検証に用いた。その結果、構築されたモデルでは、84%の正答率でもって、術中尿量>理想体重(kg) x 12mLが推測されるとなった。