DL4jのPerceptronアルゴリズムを調べるうちに、いくつかの基本的事項について、再度、確認しておく。

◎出力関数
1) ソフトマックス関数
ソフトマックス関数は分類問題をニューラルネットワークで解く場合に、出力層の活性化関数として用いられる関数。
http://nok-lab-life.hatenablog.com/entry/2017/12/03/174032
https://www.hellocybernetics.tech/entry/2016/11/30/012350

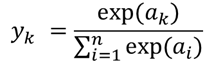
ここでyiというのは出力層のi番目のユニットの出力、Dは出力層のユニットの数である。分母に和の式を導入することで、出力層のすべてのユニットの出力の和を取ると1となってくれる。そして分母も分子もexp関数ですから正の値であり、当然分母の方が大きいためを満たしてくれる。従って、これを出力層の活性化関数に用いることで、ニューラルネットワークの出力があたかもあるクラスに属する確率を表しているとして学習させることができる。

1) ReLU(Rectified linear unit)関数
入力した値が0以下のとき0になり、1より大きいとき入力をそのまま出力する。

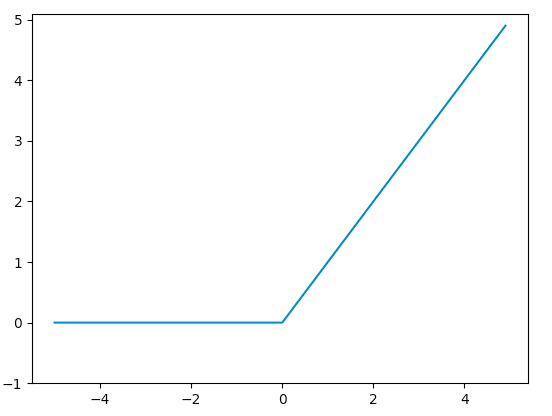
なぜ、ReLU関数が用いられるのかは、勾配消失の問題＞http://jokouprog.hatenablog.com/entry/2017/10/05/131222

◎勾配降下法
1) 確率的勾配降下法stochastic gradient descent method, SGD)
https://ja.wikipedia.org/wiki/確率的勾配降下法

2) ミニバッチ学習minibatch learning
minibatchと、エポックepochという単位。

3) 改良版勾配降下法
https://ja.wikipedia.org/wiki/確率的勾配降下法
モーメンタム法momentum
ネステロフの加速勾配法Nesterov’s accelerated gradient method

◎重みパラメータの初期値
1)Xavierの初期値
たとえば、前層から渡されるノード数がn個であるときには、標準偏差√nで割ってやります。
つまり以下の値を作用させます。
1/√n
http://el-ement.com/blog/2018/02/12/nn-introduction/
初期状態、つまり「何も知らない」 Neural Network に対する重みの選択は慎重に行う必要があります。良い方法としては、あるニューロンへの入力の重みを「平均0、分散1/n (nは入力数） の正規分布」で決定するXavierの初期値、および分散をその2倍にしたHeの初期値が知られている。