生存モデルで寿命のモデルを構築。n個体の集合で寿命t1…tnを観察した。
調査修了時に生存者がいる。反応を(ti, δi)で表すと、tiは観測個体の生存期間あるいは打ち切り時間、δ=１は死亡、δ=0は生存。ここでp個の共変量x1….xpを使って生存期間のばらつきを記述したい。
線形対数モデル：log ti= μ + β1*xi1 + ….. βp*xip + σ*εi
eiは密度f(ε)=exp(ε-eε）のガンベル分布に従うと仮定する。

＜Edmonson et al.の卵巣がん手術後の異なる化学療法の効果検証＞
log TIMEi = μ + β1*TREATi + β2*AGE + σ*εi
> data(chemotherapy)
> attach(chemotherapy)
> chemotherapy
patient time status treat age
1 1 156 1 1 66
2 2 1040 0 1 38
3 3 59 1 1 72
4 4 421 0 2 53
5 5 329 1 1 43
6 6 769 0 2 59
7 7 365 1 2 64
8 8 770 0 2 57
9 9 1227 0 2 59
10 10 268 1 1 74
11 11 475 1 2 59
12 12 1129 0 2 53
13 13 464 1 2 56
14 14 1206 0 2 44
15 15 638 1 1 56
16 16 563 1 2 55
17 17 1106 0 1 44
18 18 431 1 1 50
19 19 855 0 1 43
20 20 803 0 1 39
21 21 115 1 1 74
22 22 744 0 2 50
23 23 477 0 1 64
24 24 448 0 1 56
25 25 353 1 2 63
26 26 377 0 2 58

survivalパッケージのsurvreg()関数を使ってモデルを当てはめる。

> survreg(Surv(time,status)~factor(treat)+age,dist=”weibull”)
Call:
survreg(formula = Surv(time, status) ~ factor(treat) + age, dist = “weibull”)

Coefficients:
(Intercept) factor(treat)2 age
10.98683919 0.56145663 -0.07897718

Scale= 0.5489202

Loglik(model)= -88.7 Loglik(intercept only)= -98
Chisq= 18.41 on 2 degrees of freedom, p= 1e-04
n= 26

事後密度の位置と広がりについて初期の推定値を得るために、laplace()関数を使う。survreg()関数の当てはめ結果を使って
事後モード（-0.5, 9, 0.5, -0.05)の初期値を推定する。この関数の出力はは事後モードθと分散共分散行列V

> start=c(-.5,9,.5,-.05)
> d=cbind(time,status,treat-1,age)
> fit=laplace(weibullregpost,start,d)
> fit
$mode
[1] -0.59986796 10.98663371 0.56151088 -0.07897316

$var
[,1] [,2] [,3] [,4]
[1,] 0.057298875 0.13530436 0.004541435 -0.0020828431
[2,] 0.135304360 1.67428176 -0.156631948 -0.0255278352
[3,] 0.004541435 -0.15663195 0.115450201 0.0017880712
[4,] -0.002082843 -0.02552784 0.001788071 0.0003995202

$int
[1] -25.31207

$converge
[1] TRUE

この情報を使って、rwmetrop()関数に実装されたメトロポリスランダムウェーク連鎖提案密度を求める。
提案密度は平均ゼロで分散共分散scaleVの多変量正規密度である。
scaleは尺度パラメータでランダムウェーク連鎖が20-40%の受理範囲内に収まるように指定される。
ここではscale=1.5
> proposal=list(var=fit$var,scale=1.5)
> bayesfit=rwmetrop(weibullregpost,proposal,fit$mode,10000,d)
> bayesfit$accept
[1] 0.2769

> proposal=list(var=fit$var,scale=2)
> bayesfit=rwmetrop(weibullregpost,proposal,fit$mode,10000,d)
> bayesfit$accept
[1] 0.1789
>

[1] 0.1789
> proposal=list(var=fit$var,scale=3)
> bayesfit=rwmetrop(weibullregpost,proposal,fit$mode,10000,d)
> bayesfit$accept
[1] 0.0728
>

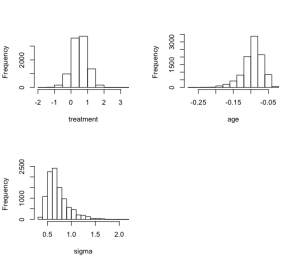
ヒストグラムを実行して,β1、β2,尺度パラメータσの周辺事後密度をシミュレーション
> par(mfrow=c(2,2))
> sigma=exp(bayesfit$par[,1])
> mu=bayesfit$par[,2]
> beta1=bayesfit$par[,3]
> beta2=bayesfit$par[,4]
> hist(beta1,xlab=”treatment”,main=””)
> hist(beta2,xlab=”age”,main=””)
> hist(sigma,xlab=”sigma”,main=””)