これまでのTensorFlowのキーポイントで、だいたい基本的なアルゴリズムを理解して、アレンジすることができるであろう。
そこで、まずは、単純なLinear Regressionを書いてみる。
Placeholderの使い方、Session ()内でのFeedの仕方、Summaryのまとめ方など、まだ少し掴みどころのないものがあるかもしれないが、あとは動かして、理解を深めればよいであろう。
y = ax + b という単純な直線回帰について、まずは、TensorBoardは考えずにコードする。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 |
import tensorflow as tf # 乱数で入力データを生成 N = 100 x = tf.random_normal([N]) a_real = tf.truncated_normal([N], seed=123, mean=1.0, stddev=0.5) b_real = tf.truncated_normal([N], seed=123, mean=2.0, stddev=0.5) # 一次回帰式 y = a * x + b y = a_real * x + b_real # パラメータ変数 a = tf.Variable(tf.random_normal([])) b = tf.Variable(tf.random_normal([])) # モデルと損失関数 model = tf.add(tf.multiply(x, a), b) loss = tf.reduce_mean(tf.pow(model - y, 2)) # 最適化アルゴリズム learn_rate = 0.1 num_epochs = 100 num_batches = N optimizer = tf.train.GradientDescentOptimizer(learn_rate).minimize(loss) # 変数を初期化 init = tf.global_variables_initializer() # セッション立ち上げ with tf.Session() as sess: sess.run(init) a_value, b_value, x_value, y_value = sess.run([a_real,b_real, x, y]) # 入力データを標準出力へ print('a_value = ', a_value, 'b_value = ', b_value, 'x_value = ', x_value, 'y_value = ', y_value) # 訓練アルゴリズム for epoch in range(num_epochs): for batch in range(num_batches): sess.run(optimizer) # 結果を標準出力へ a_final, b_final = sess.run([a, b]) print('a = ', a_final, 'b = ', b_final) |
このコードの標準出力は:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 |
a_value = [1.326649 0.67673004 1.2519947 0.66888154 0.68067974 1.839853 0.01158315 1.0966942 1.3736663 1.1960026 1.732466 0.9017789 1.0158412 0.6692703 1.3300446 1.096179 0.47501785 1.2456415 0.8835614 0.62317884 0.86885345 1.3798163 1.6583147 1.5727681 1.8461292 0.62813675 1.0586408 1.296908 1.2906543 0.31108624 0.9217831 1.7896631 1.703606 1.7858737 1.1566803 0.97074825 1.8401349 1.2074813 1.178132 0.9729775 1.2063625 1.436618 1.54302 1.1752828 0.6869371 1.4349676 0.4843803 1.3956009 0.7690195 0.324584 0.539621 1.8617102 1.4464974 1.0741993 0.48665273 1.4011142 1.3905436 1.4887097 0.7391108 0.80724233 1.1423923 0.6671516 0.85668904 1.0983977 0.58074707 0.48433417 1.5115764 0.47373134 0.41961753 0.99077857 0.8543482 0.8911292 1.2674088 1.0124779 1.9874856 0.49232167 1.4573307 0.7851268 1.1191953 0.1956408 1.3999242 0.4181654 1.4255954 1.221211 1.2630471 1.0663528 0.45448107 0.71340907 0.78816277 0.48661542 1.4900393 1.8379422 1.3991143 1.4005061 1.3932931 1.5294144 1.5392598 1.5438297 0.8769987 1.1846204 ] b_value = [2.326649 1.67673 2.2519946 1.6688815 1.6806798 2.839853 1.0115831 2.0966942 2.3736663 2.1960025 2.732466 1.9017788 2.0158412 1.6692703 2.3300447 2.096179 1.4750178 2.2456415 1.8835614 1.6231788 1.8688534 2.3798163 2.6583147 2.5727682 2.8461292 1.6281368 2.0586407 2.296908 2.2906544 1.3110862 1.9217831 2.789663 2.7036061 2.7858737 2.1566803 1.9707482 2.8401349 2.2074814 2.178132 1.9729775 2.2063625 2.436618 2.54302 2.1752827 1.6869371 2.4349678 1.4843802 2.395601 1.7690195 1.324584 1.539621 2.86171 2.4464974 2.0741994 1.4866527 2.4011142 2.3905435 2.4887097 1.7391108 1.8072424 2.1423922 1.6671516 1.856689 2.0983977 1.5807471 1.4843342 2.5115764 1.4737313 1.4196175 1.9907786 1.8543482 1.8911293 2.2674088 2.0124779 2.9874856 1.4923217 2.4573307 1.7851268 2.1191955 1.1956408 2.399924 1.4181654 2.4255953 2.221211 2.263047 2.0663528 1.4544811 1.7134091 1.7881627 1.4866154 2.4900393 2.8379421 2.3991141 2.4005063 2.3932931 2.5294144 2.53926 2.5438297 1.8769988 2.1846204] x_value = [-0.09231008 1.0855889 -0.43433964 0.6707218 -1.0305201 2.034448 0.41368032 -0.60824543 1.0065421 0.01425526 1.1110084 2.7672353 0.859031 -2.6010704 2.2298074 1.5587605 0.6486767 -0.3918182 0.03712625 -1.4642048 1.2242433 2.6017838 -0.39365187 -1.5816551 0.6466187 2.041991 -1.4988339 0.84230906 -0.3569571 0.3731087 -0.90077764 -1.3975755 0.7190008 -0.91975975 -0.02832626 0.90727234 -0.48704988 -1.0150082 -2.321191 -0.28803873 -1.4529393 0.26401109 -0.4307428 0.5003817 -0.7158611 0.78780687 0.45577294 0.8770861 0.5144365 0.58442014 -0.9576149 -0.31123543 -0.7763137 0.14826132 -0.6276706 0.03591552 -0.3434228 -0.3776658 -0.29329062 0.15592426 -0.58498174 -0.18438649 0.69946617 -1.7494621 2.1738703 0.50134933 1.0366391 -0.72730845 -0.11787201 -0.08727485 -0.7962338 0.53102994 -0.23028928 0.32886267 0.3952184 0.18132208 0.41557643 1.3113774 0.5632978 0.1356041 0.31649 -0.48323488 -0.5552353 -1.7473876 -0.04666808 0.9808306 0.61923134 -1.6188087 -1.6397622 0.5511873 0.8116867 1.0300299 0.23895128 -0.3443828 0.05640506 0.23773786 -0.9268613 0.3168603 1.4148934 0.7792227 ] y_value = [ 2.039956 2.471879 5.1278954 1.4274445 0.98279536 1.5049248 1.6758792 1.4568521 5.7849684 2.465848 1.1838633 1.24967 3.4296513 1.1531539 1.0103786 1.8216333 1.7100407 2.349721 1.426135 0.6898669 1.2808721 3.2869647 1.4019508 1.7098147 3.371813 4.84823 1.0794731 1.4732311 1.9127958 1.4369173 1.9194809 1.5881312 0.38489908 4.302853 0.9868343 1.6375351 2.9462202 3.5174186 1.7189698 1.2166415 -0.3525229 1.4811182 2.4969723 0.28664863 1.7653491 2.807786 2.583896 0.78649944 3.0822248 2.0417695 1.0362663 2.639449 1.4108918 1.0913 0.66815674 1.8731337 2.0891995 2.7020514 4.3283834 1.0184219 2.5953176 4.3706627 3.6935787 3.4044886 2.6359134 1.1218184 -0.35363746 3.413061 1.3878336 0.6158372 6.121844 4.3196154 2.1446893 1.8476038 4.390691 0.72680634 1.8897862 4.013748 1.6733935 1.7196813 -0.59811544 -0.10295534 0.87035763 1.2344656 1.7092555 4.040079 2.1447577 1.6141943 1.1943771 1.9436827 1.8399373 2.2263834 1.8486059 1.9031076 3.5375865 2.0378175 1.6591477 -0.29784137 2.4796238 1.4309907 ] a = 1.0319816 b = 2.0251942 |
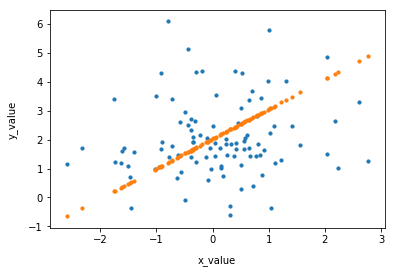
Matplotlibで散布図を描くと
|
1 2 3 4 5 6 7 8 9 10 11 |
import matplotlib import matplotlib.pyplot as plt %matplotlib inline plt.scatter(x_value, y_value, s=10) plt.xlabel("x_value", labelpad=10) plt.ylabel("y_value", labelpad=10) plt.scatter(x_value, a_final * x_value + b_final, s=10) <matplotlib.collections.PathCollection at 0x7f073d3e74e0> |
次に、Tensorboardへの解析サマリー出力を組み込んでみる。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 |
import tensorflow as tf # 乱数で入力データを生成 N = 100 x = tf.random_normal([N]) a_real = tf.truncated_normal([N], seed=123, mean=1.0, stddev=0.5) b_real = tf.truncated_normal([N], seed=123, mean=2.0, stddev=0.5) # 一次回帰式 y = a * x + b y = a_real * x + b_real # パラメータ変数 a = tf.Variable(tf.random_normal([])) b = tf.Variable(tf.random_normal([])) # パラメータをTesnorBoardでモニター step_var = tf.Variable(0, trainable=False) summary_a = tf.summary.scalar('a', a) summary_b = tf.summary.scalar('b', b) # モデルと損失関数 model = tf.add(tf.multiply(x, a), b) loss = tf.reduce_mean(tf.pow(model - y, 2)) summary_op = tf.summary.scalar('loss', loss) # 最適化 learn_rate = 0.1 num_epochs = 100 num_batches = N optimizer = tf.train.GradientDescentOptimizer(learn_rate).minimize(loss, global_step=step_var) # 変数の初期化 init = tf.global_variables_initializer() summary = tf.summary.merge_all() # セッション立ち上げ with tf.Session() as sess: writer = tf.summary.FileWriter('logs', sess.graph) sess.run(init) a_value, b_value, x_value, y_value = sess.run([a_real,b_real, x, y]) # 入力データを標準出力へ print('a_value = ', a_value, 'b_value = ', b_value, 'x_value = ', x_value, 'y_value = ', y_value) # 訓練アルゴリズム for epoch in range(num_epochs): for batch in range(num_batches): _, summary_op2, step, summary_a2, summary_b2 = sess.run([optimizer, summary_op, step_var, summary_a, summary_b]) writer.add_summary(summary_op2, global_step=step) writer.add_summary(summary_a2, global_step=step) writer.add_summary(summary_b2, global_step=step) writer.flush() writer.close() # 結果を標準出力へ a_final, b_final = sess.run([a, b]) print('a = ', a_final, 'b = ', b_final) |
出力結果は、
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 |
a_value = [1.326649 0.67673004 1.2519947 0.66888154 0.68067974 1.839853 0.01158315 1.0966942 1.3736663 1.1960026 1.732466 0.9017789 1.0158412 0.6692703 1.3300446 1.096179 0.47501785 1.2456415 0.8835614 0.62317884 0.86885345 1.3798163 1.6583147 1.5727681 1.8461292 0.62813675 1.0586408 1.296908 1.2906543 0.31108624 0.9217831 1.7896631 1.703606 1.7858737 1.1566803 0.97074825 1.8401349 1.2074813 1.178132 0.9729775 1.2063625 1.436618 1.54302 1.1752828 0.6869371 1.4349676 0.4843803 1.3956009 0.7690195 0.324584 0.539621 1.8617102 1.4464974 1.0741993 0.48665273 1.4011142 1.3905436 1.4887097 0.7391108 0.80724233 1.1423923 0.6671516 0.85668904 1.0983977 0.58074707 0.48433417 1.5115764 0.47373134 0.41961753 0.99077857 0.8543482 0.8911292 1.2674088 1.0124779 1.9874856 0.49232167 1.4573307 0.7851268 1.1191953 0.1956408 1.3999242 0.4181654 1.4255954 1.221211 1.2630471 1.0663528 0.45448107 0.71340907 0.78816277 0.48661542 1.4900393 1.8379422 1.3991143 1.4005061 1.3932931 1.5294144 1.5392598 1.5438297 0.8769987 1.1846204 ] b_value = [2.326649 1.67673 2.2519946 1.6688815 1.6806798 2.839853 1.0115831 2.0966942 2.3736663 2.1960025 2.732466 1.9017788 2.0158412 1.6692703 2.3300447 2.096179 1.4750178 2.2456415 1.8835614 1.6231788 1.8688534 2.3798163 2.6583147 2.5727682 2.8461292 1.6281368 2.0586407 2.296908 2.2906544 1.3110862 1.9217831 2.789663 2.7036061 2.7858737 2.1566803 1.9707482 2.8401349 2.2074814 2.178132 1.9729775 2.2063625 2.436618 2.54302 2.1752827 1.6869371 2.4349678 1.4843802 2.395601 1.7690195 1.324584 1.539621 2.86171 2.4464974 2.0741994 1.4866527 2.4011142 2.3905435 2.4887097 1.7391108 1.8072424 2.1423922 1.6671516 1.856689 2.0983977 1.5807471 1.4843342 2.5115764 1.4737313 1.4196175 1.9907786 1.8543482 1.8911293 2.2674088 2.0124779 2.9874856 1.4923217 2.4573307 1.7851268 2.1191955 1.1956408 2.399924 1.4181654 2.4255953 2.221211 2.263047 2.0663528 1.4544811 1.7134091 1.7881627 1.4866154 2.4900393 2.8379421 2.3991141 2.4005063 2.3932931 2.5294144 2.53926 2.5438297 1.8769988 2.1846204] x_value = [-2.570106 -1.1354795 -0.31520382 1.5109817 -0.70087165 1.1903588 -0.70775163 -0.563862 -0.5496297 1.8022655 -1.2683226 0.26913556 0.5606338 -1.6134005 -1.0696993 0.64509207 -0.6780185 -1.5630443 -1.3254148 0.15101494 -2.172791 -0.01978423 -0.67908734 0.33277237 1.6900924 -0.8792505 -2.6460338 0.26911113 0.24950111 -0.09649917 0.269038 0.6392326 1.30174 -0.02160365 -1.9225711 -0.85559165 -0.01948331 -0.26425576 0.34779334 -0.26964986 0.9273453 0.29208657 -0.22494781 -1.5534855 -0.22789182 0.10982556 -0.44970354 -0.72015846 0.77549946 0.30512765 -0.26139086 -2.0918534 0.20176168 1.0588577 1.5363158 0.4695394 0.6965151 0.7113346 0.7053652 -1.0359992 -1.23246 1.1872324 -0.07352122 -0.7811833 -1.2478086 -0.01664495 0.98153865 -0.430022 -0.6184272 0.37817347 -0.0694054 -1.8106952 0.76580334 -1.1109468 -0.5466375 -2.8442638 -0.9345467 -1.6569902 -0.3085184 1.7359804 0.06375808 -1.6100821 0.5757146 -1.3720886 -0.5662071 0.18843582 0.6184185 0.13460036 0.14462048 -0.38324443 1.4670684 -0.6443007 -0.8610103 0.46710464 -0.2595074 0.9565643 0.8340288 0.51290905 0.98214084 -0.4776315 ] y_value = [-1.0829794 0.90831697 1.8573611 2.6795492 1.2036107 5.029938 1.0033851 1.47831 1.6186585 4.3515167 0.5351403 2.1444795 2.5853562 0.5894693 0.907297 2.8033154 1.152947 0.29864872 0.712476 1.7172881 -0.01898348 2.3525176 1.5321742 3.096142 5.966258 1.0758471 -0.7425587 2.6459203 2.612674 1.2810667 2.1697779 3.9336739 4.921258 2.7472923 -0.06711984 1.1401842 2.804283 1.8883975 2.5878785 1.7106142 3.325077 2.856235 2.195921 0.3494979 1.5303898 2.5925639 1.2665527 1.3905473 2.3653936 1.4236236 1.398569 -1.0327146 2.7383451 3.2116237 2.234305 3.0589926 3.359078 3.5476804 2.260454 0.97094 0.7344394 2.4592156 1.7937042 1.2403477 0.85608596 1.4762725 3.9952471 1.2700164 1.1601146 2.3654647 1.7950518 0.27756596 3.2379947 0.88766885 1.9010515 0.09202898 1.0953871 0.48417938 1.7739031 1.5352694 2.4891806 0.74488485 3.2463312 0.54560137 1.5479007 2.267292 1.7355406 1.8094342 1.9021472 1.3001227 4.676029 1.6537546 1.1944623 3.0546892 2.0317233 3.9923978 3.823047 3.3356738 2.7383351 1.6188084 ] a = 1.0323347 b = 2.0157561 |
TensorBoardによるGraphは、
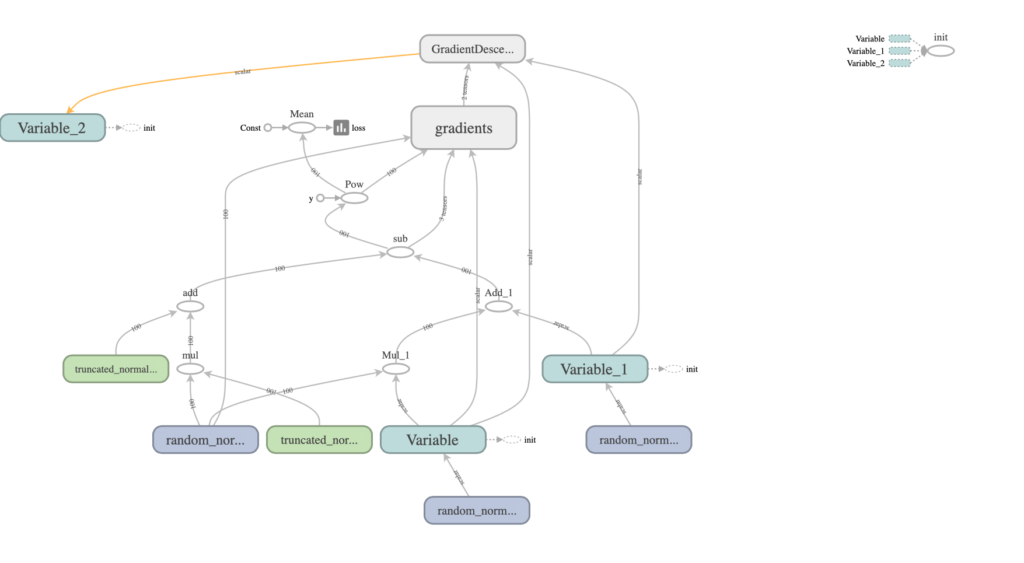
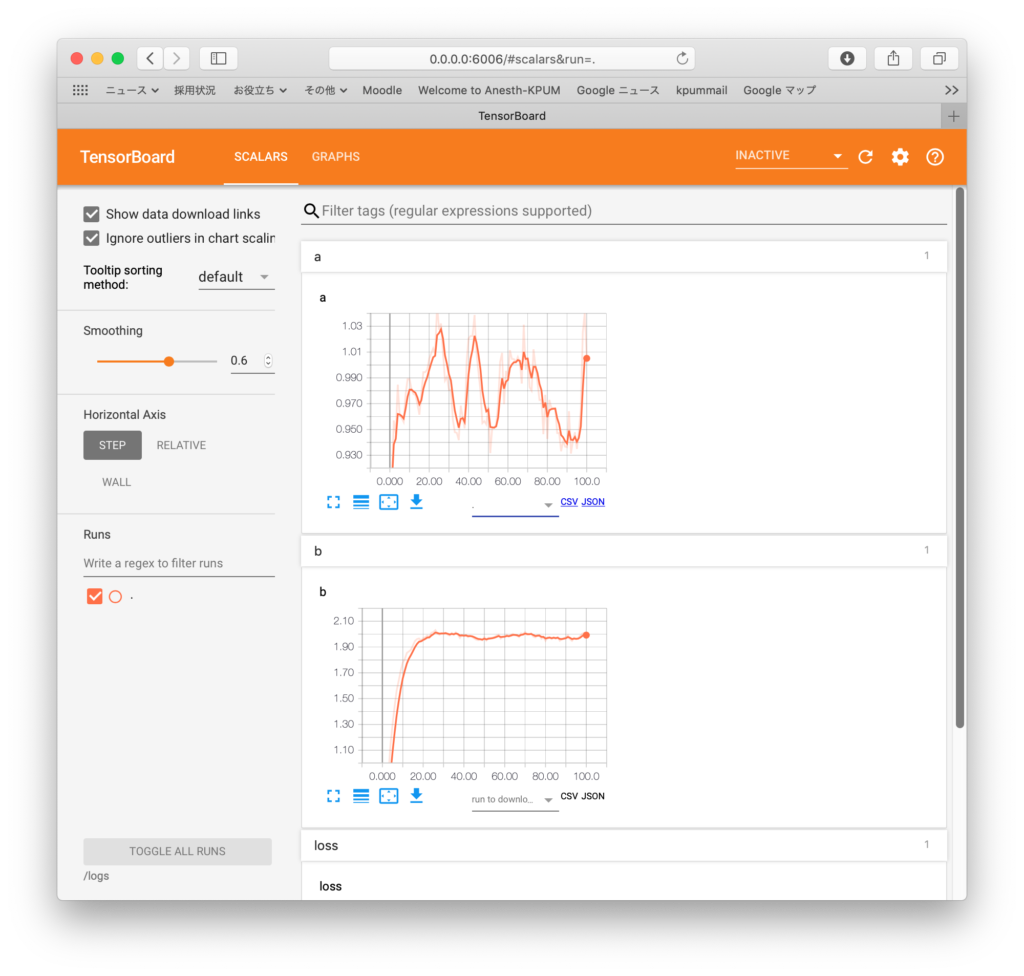
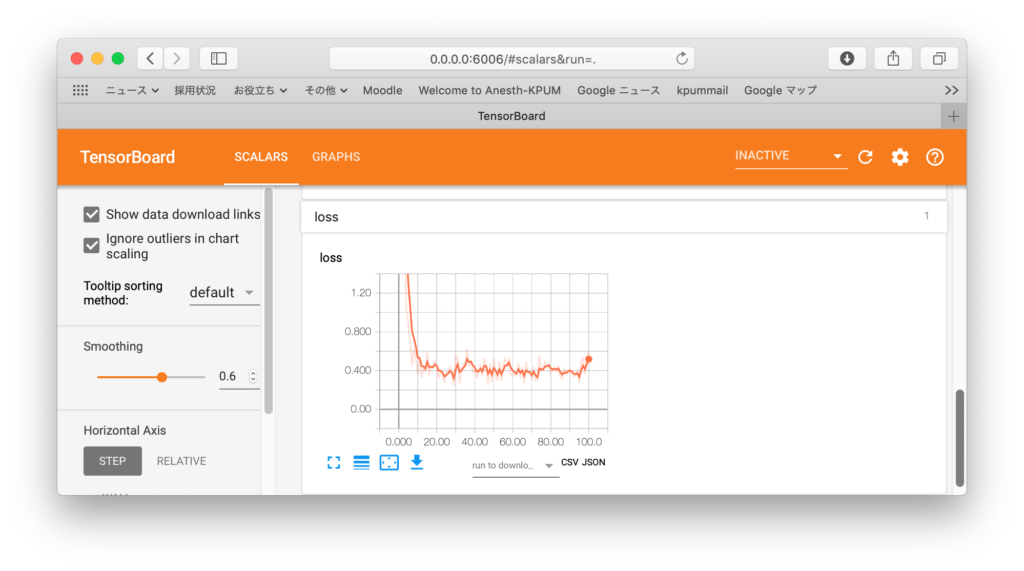
モニター値であるパラメータa, bと損失関数lossが最適化されていく状況は: