ここまで早急にDeep Learning実装に向けた強化学習を行ってきた。Rで始まり、Python & TensorFlow に移行し、そしてJava + DL4jで進めてきた。Rの利点は、DL学習が非常に分かりやすい。一方、あくまで静的な解析には良さそうだが、動的な解析にはちょっと不向きなような気がした。PythonはDL学習の花形であり、大人気でもあり参考図書も豊富であるが、慣れの問題だろうが私はなんとなく言語的に馴染みが薄い。Java + DL4jは、日本語参考資料は少なく、なかなかハードな道のりだが、言語的に馴染み良いことと、理解すると得られるものが大きいし、実装向きである。。。というのがここまでの印象。
ーーーーーーーーーーーーーーーーーーーーーーーーーー
Rでの学習にはRStudio、PythonではAnaconda+Jupiter Notebookが必須であろう。Javaの場合、DL4jをベースに学習することになるが、学習環境としてはDokcer+Zeppellinかもしれないが、Pythonのようにインタープリター的動作が不向きなこともあって、統合開発環境Eclipse、もしくはIntelliJ IDEAのほうが効率的ではないか。今回はIntelliJ IDEAを使ってみたが、Eclipseとの比較において、非常に使いやすいと感じた。ずれにせよ、関連ライブラリーの開発環境を整える上で、Apache Mavenの知識は必須である。

ーーーーーーーーーーーーーーーーーーーーーーーーーー
秋の夜長を利用して、もう一度、DL学習の基本を整理しておく。

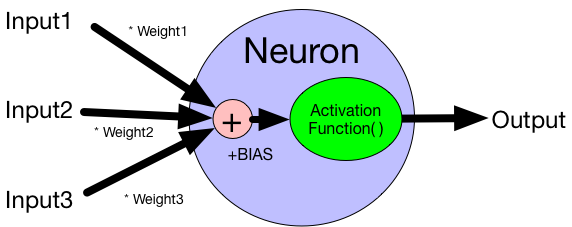
ニューラルネットワークの最小構成単位は、一つのニューロン。ニューロンには、複数の入力Inputに対して、単一の出力Outputがある。それぞれの入力値には、それぞれの重みWeightが乗じられ、ニューロンに共通のバイアス値BIASが加算されて、それらが合算されて活性化関数Activation Function()への入力値となる。

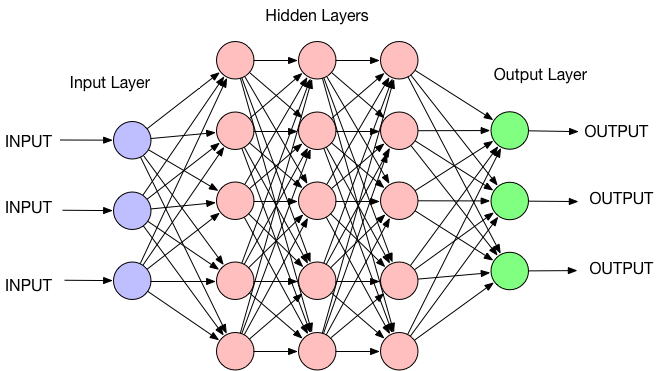
その結果、活性化関数は出力値を生成する。多層ニューラルネットワークは、複数個ｘ複数列のニューロン単位で構成される。
ーーーーーーーーーーーーーーーーーーーーーーー
Activation Functions 活性化関数
ニューロンへのそれぞれの入力値に、それぞれの重み係数wを掛け合わせて総和を求め、バイアス値を足したものをxとして、活性化関数y=F(x)へ入力して、出力値yを得る。この活性化関数には、以下の7種類のうち、どれかが利用される。
? ステップ関数

? シグモイド関数

? ハイポボリックタンジェントtanh

? ランプ関数ReLU

? Leaky ReLU

? Linear　入力値をそのまま返す。

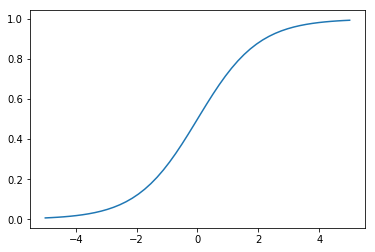
? Softmax関数：出力値の総和が１となる。
np.exp(x)/np.sum(np.exp(x))

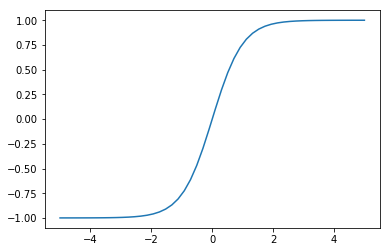
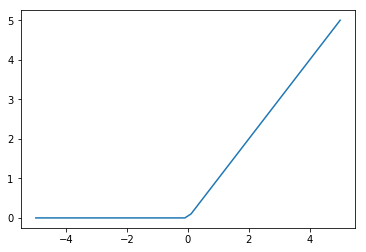
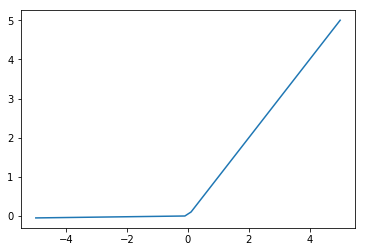
一般的に、回帰分析の出力層にはLinear、二値分類の出力層にはシグモイド、LSTM層にはtanh、多クラス分類の出力層にはソフトマックス関数、CNN層や多層パーセプトロン層では、ReLU関数が使用されるようだ。

ここで、あと重要なことは、重みパラメータの初期値には、ReLU関数の場合にはHe初期値、他はXavierザビエル値が用いられる。バイアス値の初期値はゼロとされる。

ーーーーーーーーーーーーーーーーーーーーーーーーーーー
Back propagation 逆伝搬法
ニューラルネットへの入力から出力という順伝搬で得られた出力結果と予め解っている正解との差を「誤差」と算定して、逆にニューラルネットの重みとバイアス値を誤差を少なくする方向で、逆伝搬方向に調整していく。この逆伝搬による重みとバイアス値の調整と、順伝搬を繰り返すことで、出力結果の誤差を少なくして、正解に近づける。

Loss Function 損失関数（コスト関数）
出力値と正解の誤差を定義する関数。Squared Loss二乗和誤差法、もしくはCross-Entropy交差エントロピー法が選択される。

ーーーーーーーーーーーーーーーーーーーーーーーーーーー
Gradient Descent 勾配下降法
重みとバイアスという２つのパラメータを少しずつ変化させて誤差を少なくするための最適化法には、変化量に対する偏微分勾配を求めて、誤差を最小値に近づけていく方向でパラメータを変化させる。
ここで、局所最適解という偽りの最小値に囚われないで、適切な本来の最小値（大域最適解）に近づくため、様々な最適化アルゴリズムが用いられる。
Stochastic gradient descent (SGD)確率的勾配下降法は、更新ごとにランダムにサンプルを選択する。Momentum法は、SGD法に慣性項を付加したものである。AdaGrad法は、更新が進むと学習率が小さくなる方法で、他にこれを改良したRMSProp法などがある。ここで重要なパラメータとして、誤差の大きさから算定された変化量の何パーセントを適応されるかを決めるLearning rate学習係数があり、学習の速度を決める。通常、0.1〜0.01程度の値を用いる。

ーーーーーーーーーーーーーーーーーーーーーーーーーーー
Regularization正則化
重みに制限を加えることで、局所最適解に陥ることを防止する。誤差に重みの二乗項（二乗ノルム、L2ノルム）を付加し、誤差と共に重みを減衰させる。

ーーーーーーーーーーーーーーーーーーーーーーーーーーー
Batch バッチ学習
バッチサイズは重みとバイアスの更新を行う間隔を規定する訓練データ数である。すべての訓練データを学習する学習サイクルを1 epoch エポックと呼ぶ。したがって、バッチサイズにより、1 epochにアプライされるバッチ数は複数になり得る。バッチサイズより、学習法は、以下の３通りになる。

バッチ学習：バッチサイズが全訓練データであり、1エポックごとに重みとバイアスを更新させる。
オンライン学習：バッチサイズが１訓練データであり、サンプルごとに重みとバイアスを更新させる。
ミニバッチ学習：訓練データをランダムに小さなバッチサイズを持つ小集合データに分割し。これらに分割された小集合を順次、アプライして１エポックを構成させる学習方法。

ーーーーーーーーーーーーーーーーーーーーーーーーーーー
基本アーキテクチャー
DLの基本アーキテクチャーは以下のようなものを把握しておけばよいであろう。
Deep Belief Network（DBNs)
Convolutional Neural Networks (CNNs)
Recurrent Neural Networks (RNNs)
RNN-Long Short-Term Memory (LSTM)

ーーーーーーーーーーーーーーーーーーーーーーーーーーー
以上、急ぎ足一夜でDLの基本を復習した。